Tổng hợp các cách tính diện tích chóp cụt đều và chóp cụt bất kỳ, dễ nhớ và dễ hiểu

Trong hình học không gian, khái niệm diện tích chóp cụt thường khiến nhiều học sinh bối rối bởi cấu trúc hình và công thức tính khá phức tạp. Tuy nhiên, nếu hiểu rõ bản chất, bạn sẽ thấy đây là dạng bài rất thực tế và có nhiều ứng dụng trong đời sống. Bài viết này sẽ giúp bạn hiểu rõ định nghĩa, công thức và cách vận dụng diện tích chóp cụt một cách đơn giản, dễ nhớ.

Chóp cụt là gì?

Trong hình học, chóp cụt là hình được tạo thành khi ta cắt một hình chóp bởi một mặt phẳng song song với đáy, giữ lại phần nằm giữa hai mặt phẳng song song đó. Nói cách khác, nếu ta có một hình chóp (tam giác, tứ giác, ngũ giác...) và cắt nó bằng một mặt phẳng song song với đáy, phần còn lại ở giữa chính là hình chóp cụt.

Mỗi hình chóp cụt gồm:

• Hai mặt đáy song song (một đáy lớn và một đáy nhỏ).
• Các mặt bên là các hình thang.
• Chiều cao là đoạn vuông góc giữa hai mặt đáy.

Ví dụ:

• Cắt một hình chóp tam giác sẽ được chóp cụt tam giác.
• Cắt một hình chóp vuông sẽ được chóp cụt vuông.

Khái niệm này thường gặp trong chương trình hình học không gian lớp 12, và là nền tảng để học sinh tính thể tích hoặc diện tích chóp cụt trong các bài tập thực hành.

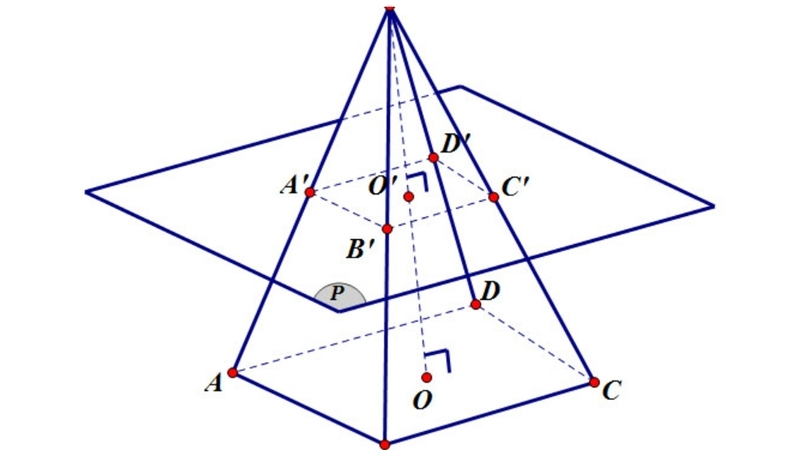
Diện tích chóp cụt là gì?

Diện tích chóp cụt là tổng diện tích của tất cả các mặt cấu thành hình, bao gồm:

• Hai đáy song song (đáy lớn và đáy nhỏ).
• Các mặt bên (thường là hình thang).

Tùy loại hình chóp cụt, ta có thể chia nhỏ thành:

• Diện tích xung quanh chóp cụt: tổng diện tích các mặt bên.
• Diện tích toàn phần chóp cụt: gồm diện tích xung quanh cộng với hai đáy.

Ví dụ, nếu ta cắt một hình chóp đều (các cạnh bên bằng nhau), phần chóp cụt thu được cũng có các mặt bên là hình thang cân – dễ tính toán hơn so với hình bất kỳ.

Công thức tính diện tích chóp cụt

Công thức sẽ thay đổi tùy theo dạng hình chóp cụt, nhưng về cơ bản, ta có thể tính bằng cách tách riêng phần đáy và phần mặt bên.

Diện tích toàn phần chóp cụt bất kỳ

S = S₁ + S₂ + S_xq

Trong đó:

• S là diện tích toàn phần chóp cụt.
• S₁ và S_2, là diện tích hai mặt đáy.
• S_xq là diện tích xung quanh (tổng diện tích các mặt bên).

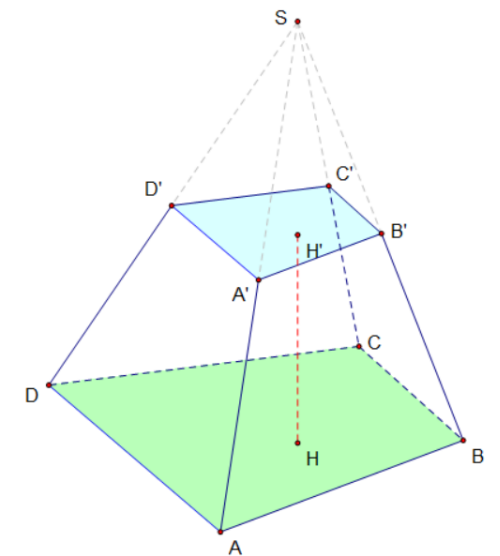
Diện tích xung quanh của chóp cụt đều

Với chóp cụt đều (có hai mặt đáy là đa giác đều và các mặt bên là hình thang cân), công thức được rút gọn như sau:

S_xq = 1/2(P₁ + P₂) x l

Trong đó:

• P₁ và P₂ là chu vi 2 mặt đáy
• l là đường sinh (cạnh bên nghiêng của hình thang bên).

Công thức này tương tự công thức tính diện tích xung quanh hình trụ hoặc hình nón cụt, chỉ khác ở dạng mặt bên.

Ví dụ minh họa

Giả sử ta có một chóp cụt đều có:

• Đáy lớn là hình vuông cạnh 10 cm.
• Đáy nhỏ là hình vuông cạnh 6 cm.
• Cạnh bên (đường sinh) dài 8 cm.

Ta có:

• P₁ = 4 x 10 = 40 cm²
• P₂ = 4 x 6 = 24 cm

⇒ S_xq = 1/2(40 + 24) x 8 = 256 cm²

Hai mặt đáy có diện tích:

• S₁ = 10² = 100 cm²
• S₂ = 6² = 36 cm²

Vậy diện tích toàn phần là: S = S₁ + S₂ + S_xq = 100 + 36 +256 = 392 cm².

Ứng dụng của diện tích chóp cụt trong thực tế

Dù xuất phát từ kiến thức hình học, diện tích chóp cụt lại có rất nhiều ứng dụng trong đời sống, kỹ thuật và giáo dục. Việc hiểu và vận dụng đúng công thức này không chỉ giúp học tốt môn Toán mà còn hỗ trợ tính toán chính xác trong nhiều lĩnh vực nghề nghiệp.

Trong xây dựng và kiến trúc

Trong ngành xây dựng, chóp cụt xuất hiện ở khắp nơi, từ mái nhà, bậc thang, đến chân trụ của các công trình. Những chi tiết có dạng loe, vát hay thu nhỏ dần lên trên đều có thể được xem là hình chóp cụt.

Ví dụ quen thuộc có thể kể đến:

• Mái nhà hình thang dốc hai bên.
• Tháp cụt trong các công trình cổ điển hoặc tôn giáo.
• Bệ tượng, chân đế cột trụ, hay bậc đỡ cầu thang.

Khi thiết kế hoặc thi công, việc tính chính xác diện tích chóp cụt giúp kỹ sư xác định lượng vật liệu cần dùng như sơn, bê tông, gạch ốp hay kim loại. Nhờ đó, công trình vừa đảm bảo thẩm mỹ, vừa tiết kiệm chi phí, tránh lãng phí nguyên liệu trong quá trình thi công.

Trong sản xuất công nghiệp và thiết kế kỹ thuật

Trong cơ khí, nội thất hay công nghệ 3D, rất nhiều sản phẩm có dạng chóp cụt như phễu, nón cụt, chi tiết loe hoặc khối bo tròn. Việc xác định đúng diện tích bề mặt chóp cụt giúp kỹ sư tối ưu hóa vật liệu, lập trình máy cắt chính xác và đảm bảo độ chính xác của sản phẩm khi gia công.

Ở lĩnh vực thiết kế kỹ thuật hoặc mô phỏng 3D, công thức tính diện tích chóp cụt còn được sử dụng để tính toán diện tích phủ vật liệu, xác định tỷ lệ phối cảnh và dựng hình khối không gian thực tế trong phần mềm chuyên dụng.

Trong học tập và giáo dục

Trong giáo dục phổ thông, diện tích chóp cụt là một phần quan trọng của chương trình hình học không gian, giúp học sinh phát triển tư duy hình học, khả năng quan sát và tưởng tượng không gian.

Nắm vững khái niệm này giúp học sinh không chỉ giải tốt bài tập mà còn hiểu sâu hơn về mối liên hệ giữa toán học và thế giới thực.

Ngoài ra, đây là dạng bài thường xuất hiện trong đề thi THPT Quốc gia, các kỳ thi học sinh giỏi hoặc trong bài tập ứng dụng công nghệ mô phỏng. Việc luyện tập công thức tính diện tích chóp cụt sẽ giúp học sinh rèn luyện tư duy logic, tính chính xác và sự cẩn trọng trong quá trình học tập.

Tạm kết

Kiến thức về diện tích chóp cụt tuy xuất phát từ toán học nhưng lại hiện diện khắp nơi trong đời sống – từ mái nhà, bậc thang, đến những công trình lớn. Việc hiểu và nắm vững công thức không chỉ giúp học tốt hơn mà còn rèn luyện tư duy logic, cẩn thận và sáng tạo – những kỹ năng quan trọng cho mọi lĩnh vực học tập và nghề nghiệp sau này.

Học hình học không gian sẽ trở nên sinh động hơn khi bạn có công cụ mạnh mẽ để trực quan hóa kiến thức. Với laptop đồ họa hiệu năng cao, bạn có thể dễ dàng sử dụng các phần mềm dựng hình 3D, mô phỏng hình chóp, khối đa diện hay mặt phẳng không gian một cách trực quan và chính xác. Hãy đầu tư ngay một chiếc laptop đồ họa để biến những công thức khô khan thành trải nghiệm học tập sống động và đầy cảm hứng.

Laptop đồ họa

Xem thêm:

Công thức tính diện tích xung quanh của hình nón là gì? Ôn tập Toán học cùng FPT Shop

Công thức tính diện tích toàn phần của hình nón là gì? Ôn tập Toán học cùng FPT Shop