Công thức tính diện tích toàn phần của hình nón là gì? Ôn tập Toán học cùng FPT Shop

Hình nón và những công thức liên quan đến hình khối này là một trong những nội dung quan trọng mà các bạn học sinh phải nắm vững khi học phân môn Hình học tại trường lớp. Nếu bạn đang muốn tìm hiểu nhiều hơn về hình nón, hãy để FPT Shop “gỡ rối” giúp bạn qua bài viết về công thức tính diện tích toàn phần của hình nón này nhé. Đây là một công thức quan trọng mà khi nắm vững, bạn sẽ hiểu hơn về hình nón nói riêng cũng như môn Hình học nói chung đấy!

Ôn tập lại về các tính chất của hình nón

Hình nón là một khối hình học không gian được tạo thành khi quay một tam giác vuông quanh một cạnh góc vuông cố định. Trong thực tế, hình nón cũng xuất hiện trong rất nhiều vật dụng và công trình kiến trúc xung quanh chúng ta, như: nón lá, phễu, tên lửa, tháp hình nón, bánh ốc quế...

Về tính chất hình khối, hình nón có các yếu tố quan trọng như sau:

• Có một đỉnh nằm trên cùng.
• Có một mặt đáy hình tròn nằm dưới.
• Mặt xung quanh của hình nón thì cong và được tạo thành khi nối tất cả các điểm trên đường tròn đáy với đỉnh của hình nón.

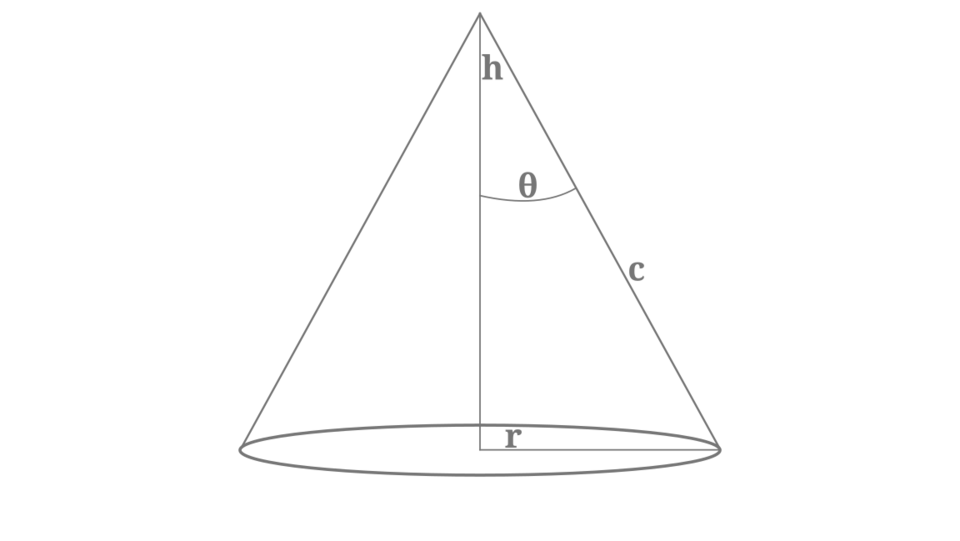
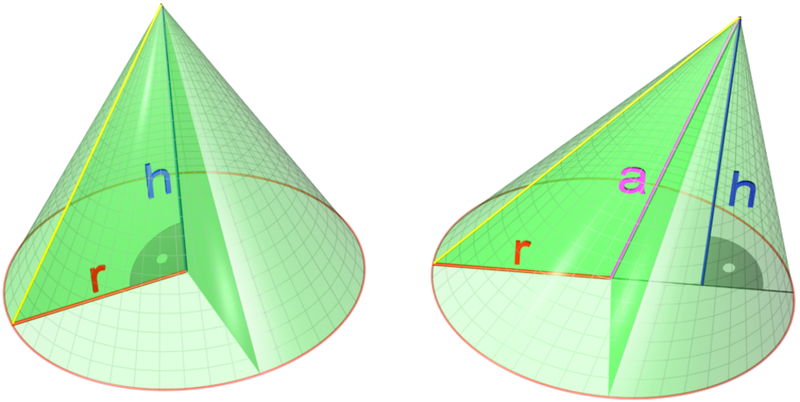
Phân tích kỹ càng hơn các yếu tố này, ta sẽ có:

• Đỉnh nằm trên cùng là điểm cố định mà các đường sinh đi qua, với đường sinh (l) là đoạn thẳng nối đỉnh đó với bất kỳ điểm nào trên đường tròn đáy.
• Chiều cao (h) của hình nón là đoạn thẳng vuông góc kẻ từ đỉnh đến tâm của mặt phẳng đáy hình tròn. Nếu xét đến tam giác vuông dùng để quay thành hình nón, chiều cao này cũng sẽ chính là độ dài của cạnh góc vuông cố định dùng để quay tam giác vuông này.
• Đáy hình tròn nằm dưới được tạo thành khi quay cạnh góc vuông còn lại của tam giác vuông nói trên.
• Bán kính đáy (r) của hình nón cũng chính là bán kính của hình tròn đáy - khoảng cách từ tâm hình tròn đáy đến một điểm bất kỳ trên đường tròn. Nếu xét đến tam giác vuông dùng để quay thành hình nón, bán kính đáy này cũng sẽ chính là độ dài của cạnh góc vuông còn lại dùng để quay tạo thành đáy hình nón.

Công thức tính diện tích toàn phần của hình nón

Để tính diện tích toàn phần của một hình khối, chúng ta cần tính riêng diện tích đáy và diện tích xung quanh rồi cộng lại. Với hình nón, đó sẽ là tổng của diện tích của mặt xung quanh và đáy hình tròn của hình khối này.

Áp dụng các tính chất hình nón nêu trên cùng các kiến thức hình học cơ bản, ta sẽ có:

• Diện tích đáy của hình nón sẽ được tính bằng công thức diện tích hình tròn là: πr² (với r là bán kính đáy)
• Diện tích xung quanh của hình nón:
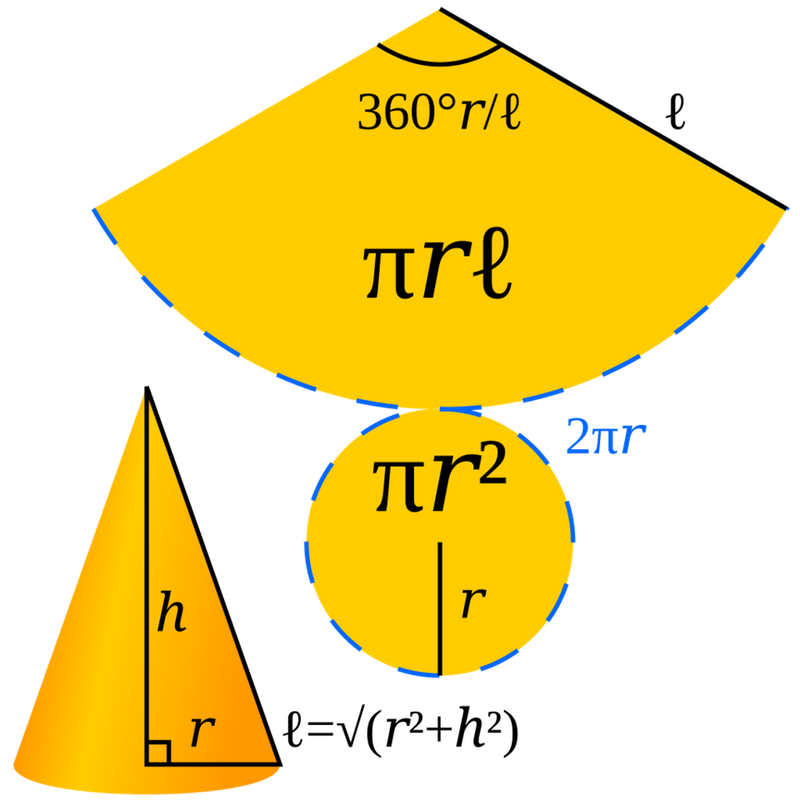
  • Nếu cắt hình nón theo một đường sinh (đường thẳng nối đỉnh với một điểm trên đường tròn đáy) rồi trải phẳng phần bên hông ra, ta sẽ được một hình quạt tròn. Hình quạt tròn này sẽ có bán kính chính là đường sinh (ℓ) của hình nón và độ dài cung tròn chính là chu vi đáy của hình nón, tức là 2πr (với r là bán kính đáy).
  • Mà diện tích hình quạt tròn thì được tính theo công thức: 

S_{hình quạt} = (độ dài cung tròn / chu vi hình tròn) x diện tích hình tròn

= (2πr / 2πℓ) x πℓ² = πrl

• Suy ra diện tích xung quanh của hình nón cũng chính là bằng diện tích của hình quạt tròn với bán kính bằng đường sinh của hình nón ấy và độ dài cung tròn bằng chu vi đáy của hình nón ấy. Nói cách khác, diện tích xung quanh của hình nón thì bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh, với π.r chính là nửa chu vi đường tròn.

Lấy hai công thức trên và cộng lại, ta sẽ có công thức tính diện tích toàn phần của hình nón:

S_tp = S_đáy + S_{xung quanh}

= πr² + πrl = πr(r + l)

Trong đó:

• π: Số pi (xấp xỉ 3.14)
• r: Bán kính đáy của hình nón
• l: Đường sinh của hình nón

Ứng dụng của tính diện tích toàn phần của hình nón

Đối với các ứng dụng như:

• Sản xuất các vật thể hình nón như nón lá, phễu, bánh ốc quế, tên lửa,...;
• Đóng gói, làm bao bì cho các vật thể hình nón đặc thù;
• Thiết kế, xây dựng các vật thể hình nón như mái nhà, đầu ống dẫn,...;
• …

Thì việc tính được diện tích toàn phần của hình nón sẽ giúp ích rất nhiều trong việc tính toán cụ thể số lượng nguyên vật liệu cần thiết, dẫn đến tiết kiệm chi phí và thời gian hơn, cũng như tạo ra các sản phẩm đồng nhất với nhau hơn.

Các bài tập vận dụng tính diện tích toàn phần của hình nón

Dưới đây sẽ là một số bài tập ví dụ yêu cầu người giải phải áp dụng công thức tính diện tích toàn phần của hình nón để tìm ra được đáp án cuối cùng. Các bài tập này đều sẽ có kèm lời giải chi tiết để bạn có thể nắm bắt được công thức này một cách tốt hơn.

• Bài tập 1: Một công ty cần làm hình nón trang trí với bán kính đáy r = 10 cm và chiều cao h = 24 cm. Họ cần dán giấy màu phủ kín toàn bộ mặt ngoài của nón (gồm cả đáy và mặt xung quanh). Biết mỗi cuộn giấy có diện tích 1000 cm². Hãy tính số cuộn giấy ít nhất mà họ cần để phủ 100 hình nón trang trí.

Cách giải:

Sử dụng tính chất của hình nón, ta thấy được là tam giác vuông dùng để quay để tạo thành hình nón này sẽ có cạnh góc vuông cố định là bán kính đáy, chiều cao sẽ là cạnh góc vuông còn lại. Suy ra, đường sinh l của hình nón sẽ là cạnh huyền của tam giác vuông này.

Sử dụng định lý Pythagoras để tính độ dài đường sinh l, ta có:

l = √(r² + h²)

= √(10² + 24²) 

= √(100 + 576) 

= √676 

= 26 (cm)

Diện tích toàn phần của 1 hình nón trang trí là:

Stp = πr² + πrl

= 3,14 x 10² + 3,14 x 10 x 26

= 3,14 x 100 + 3,14 x 260 

= 314 + 816,4 

= 1130,4 (cm²)

Vì mỗi cuộn giấy có diện tích 1000 cm², nên số cuộn giấy cần dùng cho 1 hình nón trang trí là:

Số cuộn giấy = Stp / 1000

= 1130,4 / 1000 ≈ 1,13

Làm tròn lên:

Số cuộn giấy cần dùng cho 1 hình nón trang trí = 2 cuộn

Với 100 hình nón trang trí, công ty sẽ cần:

Số cuộn giấy = 2 x 100 = 200 (cuộn)

Đáp án: Cần ít nhất 200 cuộn giấy để phủ kín 100 hình nón trang trí.

• Bài tập 2: Cho một mái nhà có dạng hình nón với bán kính đáy r = 1,5 m và chiều cao h = 4 m. Người ta muốn phủ lớp chống thấm cho toàn bộ mặt ngoài của mái (bao gồm cả đáy và mặt xung quanh). Hỏi diện tích cần phủ là bao nhiêu?

Cách giải:

Sử dụng tính chất của hình nón, ta thấy được là tam giác vuông dùng để quay để tạo thành hình nón này sẽ có cạnh góc vuông cố định là bán kính đáy, chiều cao sẽ là cạnh góc vuông còn lại. Suy ra, đường sinh l của hình nón sẽ là cạnh huyền của tam giác vuông này.

Sử dụng định lý Pythagoras để tính độ dài đường sinh l, ta có:

l = √(r² + h²)

= √(1,5² + 4²)

= √(2,25 + 16)

= √18,25 ≈ 4,27 (m)

Diện tích toàn phần của mái nhà là:

Stp = π * r² + π * r * l

= 3,14 * 1,5² + 3,14 * 1,5 * 4,27

= 3,14 * 2,25 + 3,14 * 6,405

≈ 7,065 + 20,11

= 27,175 (m²)

Đáp án: Diện tích cần phủ là 27,175 m².

Tạm kết

Trên đây là những kiến thức bổ ích về công thức tính diện tích toàn phần của hình nón cùng một số bài tập vận dụng mà FPT Shop muốn truyền tải đến bạn. Mong rằng những thông tin trong bài viết này sẽ có ích cho bạn!

Đối với các bạn học sinh trong thời đại mới ngày nay thì một chiếc điện thoại thông minh thuộc phân khúc tầm trung sẽ là vô cùng phù hợp để vừa trau dồi những kiến thức bổ ích, vừa có những phút giây giải trí nhẹ nhàng. Hãy đến ngay với FPT Shop để tham khảo ngay những mẫu sản phẩm phù hợp với lứa tuổi học sinh, điển hình như những chiếc điện thoại thuộc hãng Xiaomi nhé.

• Điện thoại Xiaomi

Xem thêm:

• Tín chỉ là gì? Ưu, nhược điểm của hình thức đào tạo tín chỉ
• Minecraft: Education Edition – Game thuộc đề tài giáo dục hấp dẫn