Công thức tính diện tích xung quanh của hình nón là gì? Ôn tập Toán học cùng FPT Shop

Hình học - đề cập đến các hình khối trong thực tiễn và các tính chất của không gian - là một trong hai phân môn vô cùng quan trọng trong Toán học cấp cao của các bạn học sinh - sinh viên. Dù có bản chất dễ tiếp cận hơn với Đại số, Hình học vẫn chứa đựng rất nhiều kiến thức mà người học cần phải nắm bắt, với hình nón là một trong những loại hình khối đặc biệt nhất trong số kiến thức ấy.

Nếu bạn đang cần giúp đỡ trong việc tìm hiểu về hình khối này, hãy để FPT Shop “gỡ rối” giúp bạn với bài viết lần này nhé. Cụ thể hơn, bài viết hôm nay sẽ đề cập đến công thức tính diện tích xung quanh của hình nón - một trong những dữ kiện quan trọng nhất khi tìm hiểu về hình khối này. Thêm vào đó, một số bài tập vận dụng cũng sẽ được trình bày đầy đủ để bạn nắm bắt công thức này dễ hơn. 

Ôn tập lại về các tính chất của hình nón

Hình nón là một khối hình học không gian được tạo thành khi quay một tam giác vuông quanh một cạnh góc vuông cố định. Trong thực tế, hình nón cũng xuất hiện trong rất nhiều vật dụng và công trình kiến trúc xung quanh chúng ta, như: nón lá, phễu, tên lửa, tháp hình nón, bánh ốc quế...

Về tính chất hình khối, hình nón có các yếu tố quan trọng như sau:

• Có một đỉnh nằm trên cùng.
• Có một mặt đáy hình tròn nằm dưới.
• Mặt xung quanh của hình nón thì cong và được tạo thành khi nối tất cả các điểm trên đường tròn đáy với đỉnh của hình nón.

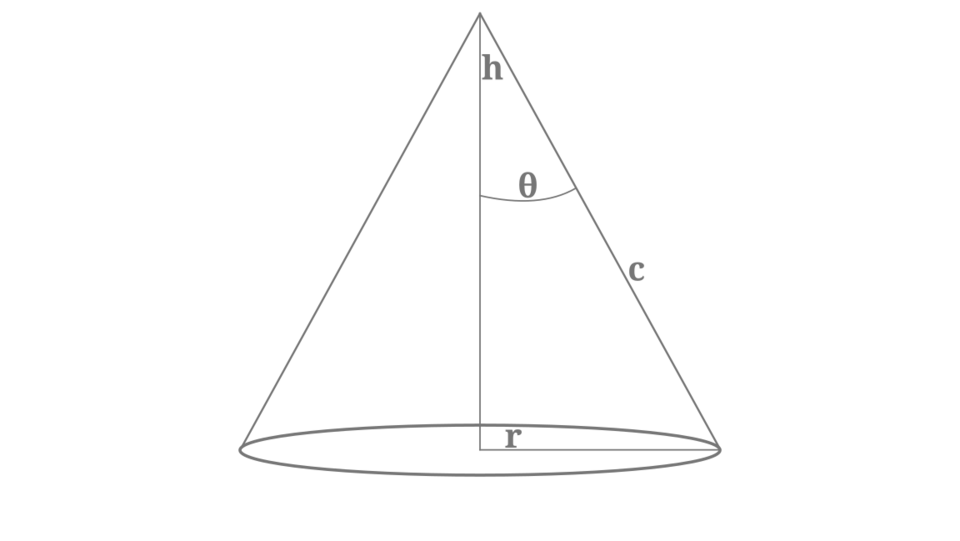
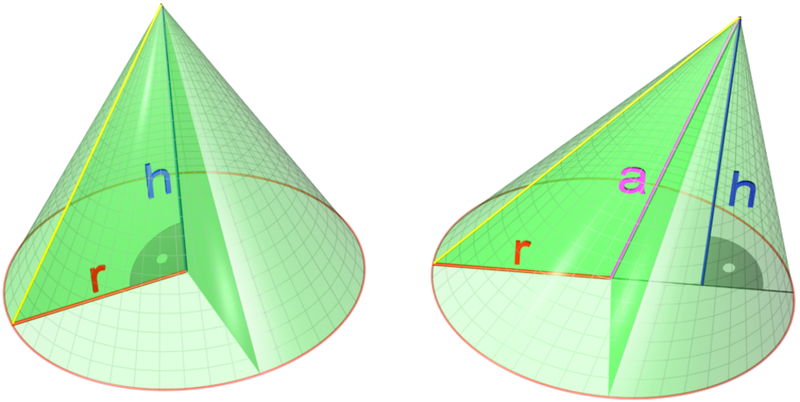
Phân tích kỹ càng hơn các yếu tố này, ta sẽ có:

• Đỉnh nằm trên cùng là điểm cố định mà các đường sinh đi qua, với đường sinh (l) là đoạn thẳng nối đỉnh đó với bất kỳ điểm nào trên đường tròn đáy.
• Chiều cao (h) của hình nón là đoạn thẳng vuông góc kẻ từ đỉnh đến tâm của mặt phẳng đáy hình tròn. Nếu xét đến tam giác vuông dùng để quay thành hình nón, chiều cao này cũng sẽ chính là độ dài của cạnh góc vuông cố định dùng để quay tam giác vuông này.
• Đáy hình tròn nằm dưới được tạo thành khi quay cạnh góc vuông còn lại của tam giác vuông nói trên.
• Bán kính đáy (r) của hình nón cũng chính là bán kính của hình tròn đáy - khoảng cách từ tâm hình tròn đáy đến một điểm bất kỳ trên đường tròn. Nếu xét đến tam giác vuông dùng để quay thành hình nón, bán kính đáy này cũng sẽ chính là độ dài của cạnh góc vuông còn lại dùng để quay tạo thành đáy hình nón.

Công thức tính diện tích xung quanh của hình nón

Nếu như ta cắt hình nón theo một đường sinh rồi trải phẳng phần mặt xung quanh ra, ta sẽ được một hình quạt tròn với:

• Bán kính của hình quạt cũng chính là đường sinh (l) của hình nón.
• Độ dài cung tròn của hình quạt cũng chính là chu vi đáy của hình nón, tức là 2πr (với r là bán kính đáy).

Mà diện tích hình quạt thì lại bằng một phần diện tích hình tròn, cụ thể là:

S_{hình quạt} = (Độ dài cung tròn / Chu vi hình tròn) x Diện tích hình tròn

= (2πr / 2πl) x πl² = πrl

Suy ra diện tích xung quanh của hình nón cũng chính là bằng diện tích của hình quạt tròn với bán kính bằng đường sinh của hình nón ấy và độ dài cung tròn bằng chu vi đáy của hình nón ấy. Nói cách khác, diện tích xung quanh của hình nón thì bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh, với π.r chính là nửa chu vi đường tròn.

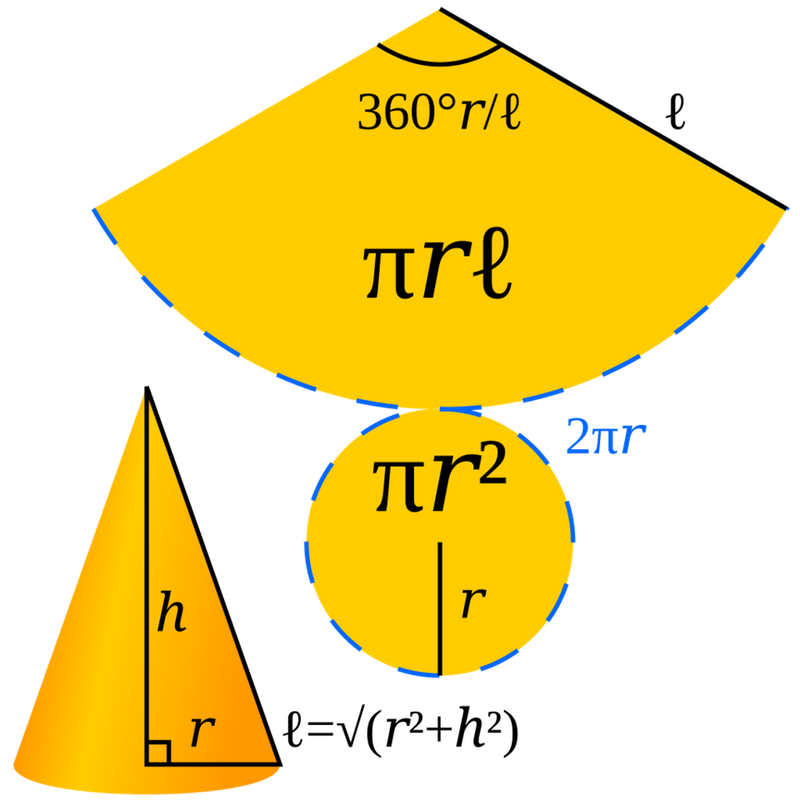
Công thức tổng quát: Sxq = πrl

Trong đó:

• π: Số pi (xấp xỉ 3.14)
• r: Bán kính đáy của hình nón
• l: Đường sinh của hình nón

Ứng dụng của tính diện tích xung quanh của hình nón

Công thức tính diện tích xung quanh của hình nón được sử dụng trong thực tế để tính diện tích bao phủ (bằng sơn màu, vật liệu,...) xung quanh các đồ vật hay công trình hình nón như: tháp hình nón, mũ sinh nhật, kem ốc quế,...

Thêm nữa, khi kết hợp với diện tích hình tròn đáy được tính bằng công thức diện tích hình tròn πr² ,công thức tính diện tích xung quanh của hình nón sẽ là một phần quan trọng để hoàn thiện công thức tính diện tích toàn phần của hình nón: 

S_tp = S_xq + S_đáy = πrl + πr² = πr x (l + r)

Trong đó:

• π: Số pi (xấp xỉ 3.14)
• r: Bán kính đáy của hình nón
• l: Đường sinh của hình nón

Người ta cần phải tính được diện tích toàn phần của hình nón để tạo nên những đồ vật hay công trình hình nón quen thuộc kể trên.

Bài tập công thức tính diện tích xung quanh của hình nón

Sau đây sẽ là một số bài tập ví dụ đòi hỏi phải áp dụng công thức tính diện tích xung quanh của hình nón để tìm ra đáp án một cách hoàn chỉnh. Các bài tập này đều sẽ được cung cấp kèm lời giải chi tiết để giúp bạn nắm bắt kiến thức một cách tốt hơn.

• Bài tập 1: Có một ngọn tháp hình nón có bán kính đáy r = 6 m và đường sinh l = 10 m. Nếu người ta muốn sơn toàn bộ mặt ngoài của tháp này thì diện tích cần sơn là bao nhiêu?

Hướng dẫn giải:

Theo dữ kiện đề cho, ta sẽ có diện tích ngọn tháp cần sơn chính là diện tích xung quanh của tháp hình nón này.

Áp dụng công thức tính diện tích xung quanh hình nón:

S_xq = πrl = 3,14 x 6 x 10 = 188,4 (m²)

Đáp số: Diện tích xung quanh cần sơn của ngọn tháp là 188,4 m².

• Bài tập 2: Một chiếc mái che hình nón được dựng với bán kính đáy r = 3 m và đường sinh l = 5 m. Người ta cần phủ bạt để che phần xung quanh của mái che. Hỏi diện tích bạt cần dùng là bao nhiêu?

Hướng dẫn giải:

Áp dụng công thức tính diện tích xung quanh hình nón:

S_xq = πrl = 3,14 x 3 x 5 = 47,1 (m²)

Đáp số: Diện tích bạt cần dùng để che phần xung quanh mái che là 47,1 m².

• Bài tập 3: Cho tam giác ABC vuông tại A có cạnh huyền BC = 20cm và cạnh AB = 16cm. Nếu quay tam giác ABC cạnh AB thì ta sẽ được một hình nón có diện tích toàn phần là bao nhiêu (làm tròn đến hàng đơn vị)?

Hướng dẫn giải:  

Khi quay tam giác ABC vuông tại A, ta sẽ có một hình nón với độ dài đường sinh l chính là cạnh BC và bán kính đáy chính là cạnh AC.

Áp dụng định lý Pytago, ta có:

BC² = AB² + AC²

⇒ AC² = BC² - AB²  = 202 - 162  = 400 - 256 = 144 (cm²) ⇒ AC = 12 (cm)

Áp dụng công thức tính diện tích toàn phần hình nón:

S_tp = S_xq + S_đáy = πrl + πr²

= (3.14 x 12 x 20) + (3.14 x 122) = 753.6 + 452.16 = 1,205.76 = 1,206 (cm²)

Đáp số: Diện tích toàn phần của hình nón này là 1,206 cm².

• Bài tập 4: Một xưởng sản xuất cần làm một mẫu nón che nắng có dạng hình nón với bán kính đáy r = 14 cm và đường sinh l = 25 cm. Biết rằng người ta sử dụng vải với khối lượng là 200 g/m². Hãy tính khối lượng vải cần dùng để làm phần xung quanh của chiếc nón. (Làm tròn kết quả đến 2 chữ số thập phân).

Hướng dẫn giải:

Áp dụng công thức tính diện tích xung quanh hình nón:

S_xq = πrl = 3,14 x 14 x 25 = 1099 (cm²) = 0,1099 (m²)

Theo dữ kiện đề bài, ta sẽ có công thức tính khối lượng vải là:

m = S x k

Trong đó:

• m là khối lượng vải (g),
• S là diện tích vải (m²),
• k là khối lượng vải trên mỗi mét vuông (g/m²).

Áp dụng các số liệu vào công thức này, ta sẽ có:

m = S x k = 0.1099 x 200 = 21,98 ̣̣(g)

Đáp số: Khối lượng vải cần dùng để làm phần xung quanh của chiếc nón là 21,98 g.

Tạm kết

Trên đây là những kiến thức bổ ích về công thức tính diện tích xung quanh của hình nón cùng một số bài tập vận dụng mà FPT Shop muốn truyền tải đến bạn. Mong rằng những thông tin trong bài viết này sẽ có ích cho bạn!

Để có thể dễ dàng nghiên cứu thông tin học tập quan trọng như công thức hình nón, cũng như để giải trí sau những giờ học tập căng thẳng, các bạn nhỏ ngày nay sẽ cần đến một thiết bị cá nhân đa năng và mạnh mẽ. Hãy đến ngay với FPT Shop để tham khảo những mẫu máy tính tân tiến với mức giá phải chăng, phù hợp với lứa tuổi học sinh - sinh viên nhé!

Xem thêm:

• Cách viết công thức toán học trong Excel cực đơn giản
• Cẩm nang công thức đạo hàm đầy đủ nhất giúp bạn giải toán dễ dàng