Các tính chất của tam giác vuông và ứng dụng phong phú trong thực tế

Việc hiểu và vận dụng đúng các tính chất của tam giác vuông không chỉ đơn thuần là việc ghi nhớ các công thức toán học mà còn đòi hỏi sự hiểu biết sâu sắc về mối quan hệ giữa các phần tử cấu thành tam giác. Bài viết này sẽ đi sâu vào những tính chất cơ bản, các định lý nền tảng, công thức tính toán quan trọng và những ứng dụng phong phú của tam giác vuông, từ đó làm nổi bật vai trò không thể thiếu của nó trong toán học và đời sống.

Tam giác vuông là gì?

Tam giác vuông được định nghĩa bởi sự hiện diện của một góc vuông (góc có số đo bằng 90 độ). Đây là đặc điểm nhận dạng cốt lõi phân biệt nó với các loại tam giác khác (tam giác nhọn, tam giác tù).

Các thành phần của một tam giác vuông bao gồm:

• Góc vuông: Là góc có số đo chính xác bằng 90 độ. Trong ký hiệu toán học, góc vuông thường được đánh dấu bằng một ký hiệu hình vuông nhỏ tại đỉnh của góc.
• Hai cạnh góc vuông (cạnh kề góc vuông): Đây là hai cạnh tạo nên góc vuông. Chúng vuông góc với nhau. Trong một tam giác vuông, hai cạnh góc vuông thường được ký hiệu là a và b.
• Cạnh huyền: Đây là cạnh dài nhất trong tam giác vuông và luôn nằm đối diện với góc vuông. Cạnh huyền thường được ký hiệu là c.
• Hai góc nhọn: Ngoài góc vuông, tam giác vuông còn có hai góc khác. Tổng số đo của ba góc trong một tam giác bất kỳ luôn bằng 180 độ. Do đó, trong tam giác vuông, tổng số đo của hai góc nhọn bằng 180°−90°=90°. Điều này có nghĩa là hai góc nhọn là hai góc phụ nhau.

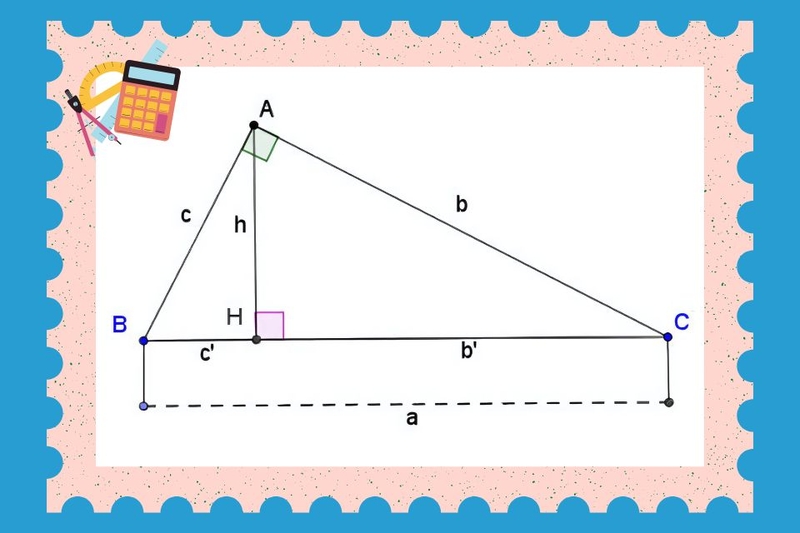
Hiểu rõ các thuật ngữ này là bước đầu tiên để tiếp cận các tính chất và định lý liên quan đến tam giác vuông. Mối quan hệ giữa độ dài các cạnh và số đo các góc là trọng tâm của nhiều định lý quan trọng.

Ví dụ minh họa:

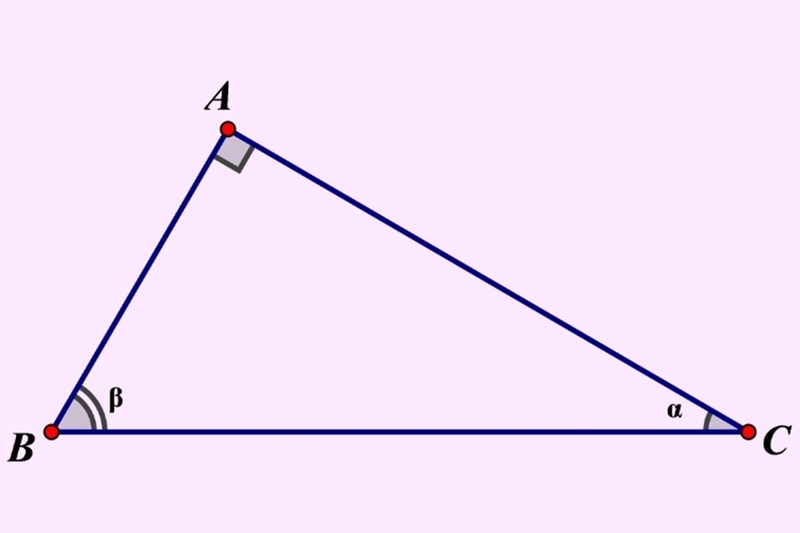
Xét tam giác ABC vuông tại A.

• Góc vuông là góc A (90°).
• Hai cạnh góc vuông là AB và AC.
• Cạnh huyền là BC.
• Hai góc nhọn là góc B và góc C. Ta có ∠B+∠C=90°.

Các tính chất cơ bản của tam giác vuông

Các tính chất cơ bản của tam giác vuông

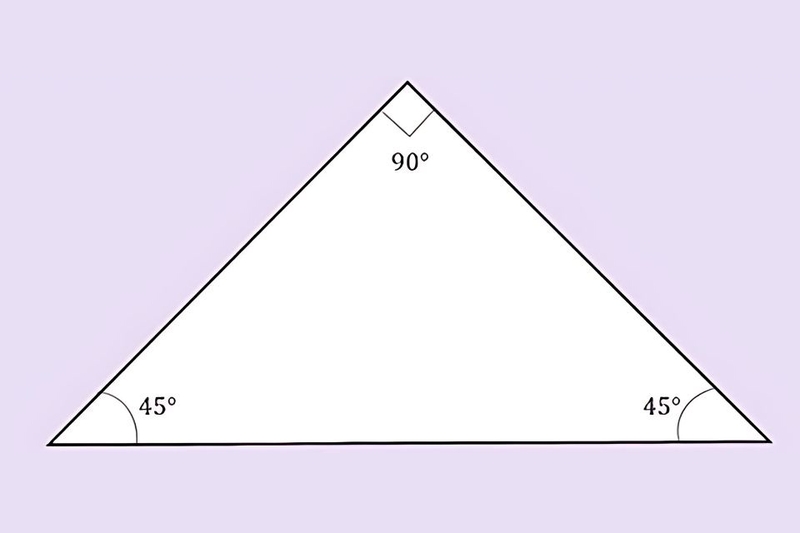
Tổng các góc

Một góc vuông (90°), hai góc còn lại là hai góc nhọn và tổng của chúng cũng bằng 90° (hai góc này gọi là góc phụ nhau)

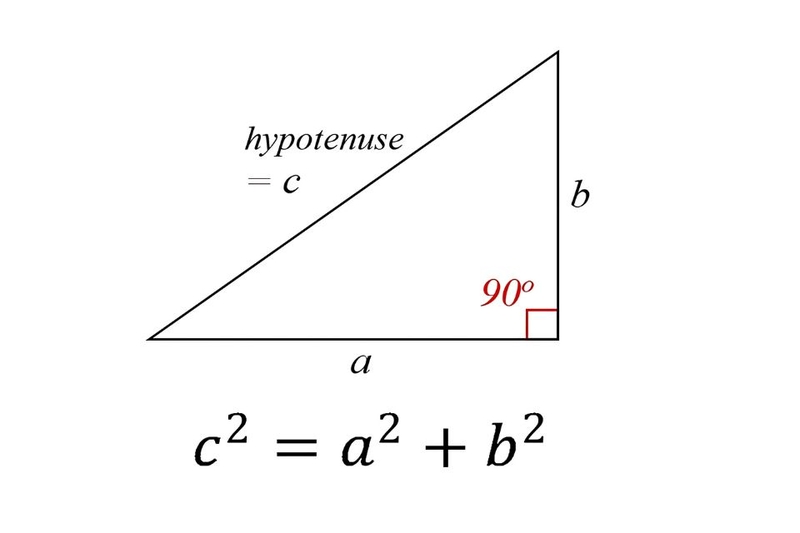
Định lý Pythagoras

Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông:$$a^2+b^2=c^2$$

Trong đó, $a$ và $b$ là hai cạnh góc vuông, $c$ là cạnh huyền.

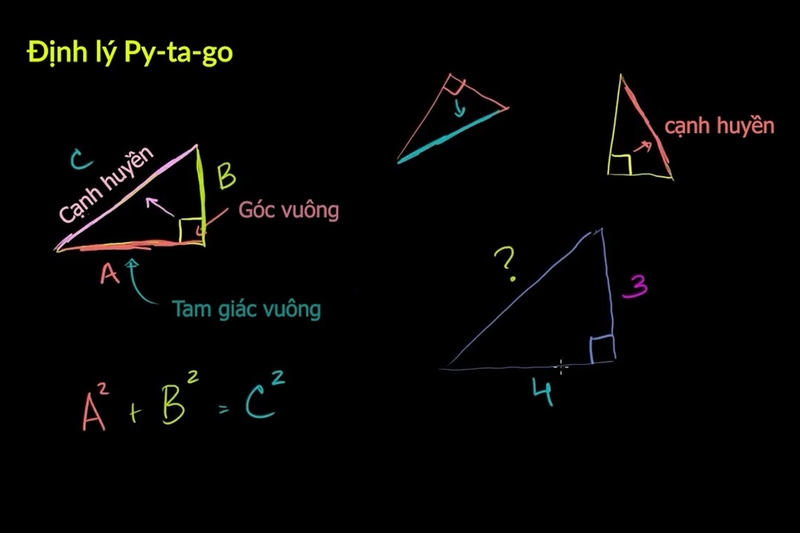
Ví dụ: Cho tam giác vuông có hai cạnh góc vuông lần lượt là 3 cm và 4 cm, cạnh huyền sẽ là:

Định lý Pythagoras đảo: Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại, thì tam giác đó là tam giác vuông. Đây là dấu hiệu nhận biết tam giác vuông khi biết độ dài ba cạnh.

Đường trung tuyến và đường cao

• Đường trung tuyến ứng với cạnh huyền trong tam giác vuông có độ dài bằng nửa cạnh huyền.
• Đường cao từ đỉnh góc vuông xuống cạnh huyền chia tam giác vuông thành hai tam giác vuông nhỏ hơn, đồng dạng với tam giác ban đầu

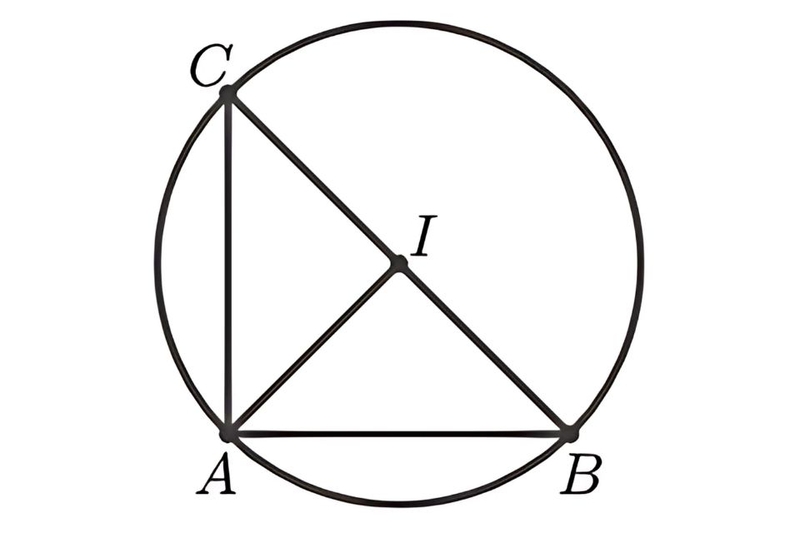
Tâm đường tròn ngoại tiếp

Tâm đường tròn ngoại tiếp tam giác vuông nằm tại trung điểm cạnh huyền. Đường kính của đường tròn ngoại tiếp chính là cạnh huyền.

Các tỉ số lượng giác

Các tỉ số sin, cos, tan, cot của một góc nhọn trong tam giác vuông được xác định bằng tỉ số giữa các cạnh:

• $\sin$sin (góc nhọn) = cạnh đối / cạnh huyền
• $\cos$cos (góc nhọn) = cạnh kề / cạnh huyền
• $\tan$tan (góc nhọn) = cạnh đối / cạnh kề

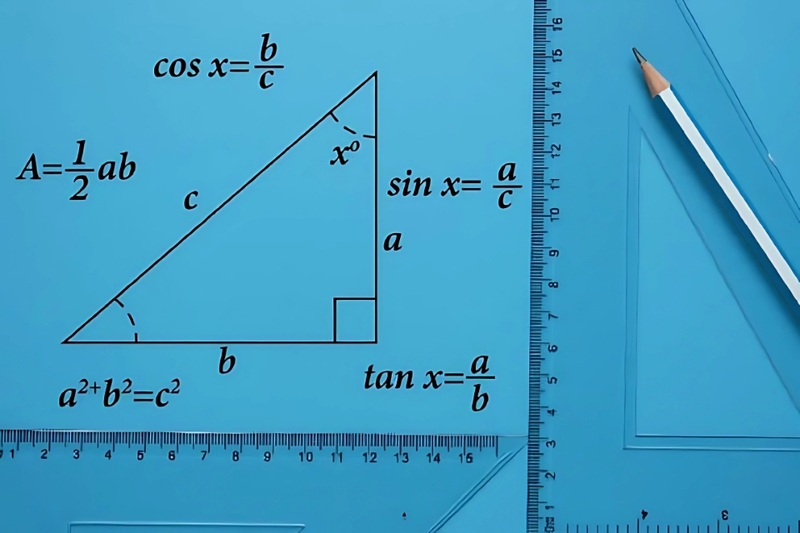
Công thức tính diện tích tam giác vuông

Việc tính diện tích của một tam giác là một bài toán cơ bản nhưng có ý nghĩa thực tiễn cao. Đối với tam giác vuông, công thức tính diện tích đặc biệt đơn giản nhờ vào cấu trúc vuông góc của nó.

Công thức cơ bản

Diện tích (S) của một tam giác vuông bằng một nửa tích độ dài của hai cạnh góc vuông.

• S=1/2 × cạnh góc vuông 1 x cạnh góc vuông 2

Nếu gọi độ dài hai cạnh góc vuông là a và b, công thức là:

• S=1/2​×a×b

Giải thích công thức

Công thức này xuất phát từ việc nhận thấy rằng một tam giác vuông có thể được coi là một nửa của một hình chữ nhật có các cạnh là hai cạnh góc vuông của tam giác đó. Diện tích hình chữ nhật là tích hai cạnh (a×b), do đó diện tích tam giác vuông là một nửa diện tích hình chữ nhật đó.

Ý nghĩa thực tiễn:

• Đo đạc diện tích: Công thức này cho phép tính toán nhanh chóng diện tích của các khu vực có hình dạng tam giác vuông, rất hữu ích trong các lĩnh vực như xây dựng, kiến trúc, quy hoạch đất đai, hoặc thậm chí là các công việc đơn giản như cắt vải, trang trí nội thất.
• Ứng dụng trong hệ tọa độ: Khi các điểm được biểu diễn bằng tọa độ, việc tính diện tích của tam giác vuông có các cạnh song song với các trục tọa độ trở nên rất dễ dàng bằng cách lấy nửa tích độ dài của các cạnh đó (độ dài bằng hiệu tuyệt đối giữa các tọa độ).
• Kết hợp với các định lý khác: Trong trường hợp không biết trực tiếp độ dài hai cạnh góc vuông, chúng ta có thể sử dụng Định lý Pythagoras hoặc lượng giác để tìm ra chúng trước, sau đó áp dụng công thức diện tích.

Ví dụ ứng dụng tính diện tích: Một mảnh đất hình tam giác vuông có hai cạnh góc vuông dài 10 mét và 15 mét. Tính diện tích mảnh đất. Áp dụng công thức: S=1/2​×10×15=1/2​×150=75m^2.

Công thức tính diện tích tam giác vuông là một công cụ đơn giản nhưng cực kỳ hiệu quả, thể hiện sự kết nối trực tiếp giữa hình học và các phép đo lường trong thế giới thực.

Khám phá các định lý và tính chất mở rộng

Việc khám phá các định lý và tính chất mở rộng của tam giác vuông không chỉ giúp người học nắm bắt được nền tảng vững chắc mà còn mở rộng tri thức ra nhiều lĩnh vực khác. Định lý Pythagoras không chỉ dừng lại ở việc khẳng định một mối quan hệ cố định giữa các cạnh của tam giác vuông mà còn tạo tiền đề để phát triển nhiều khái niệm lượng giác khác nhau. Những công thức như sin, cos, tan không những mang lại sự chính xác trong việc đo đạc mà còn áp dụng sâu rộng trong các ứng dụng phân tích và phát triển sản phẩm.

Khi học về sin, cos, tan, người học nên chú ý đến cách chúng tạo dựng một ngôn ngữ hình học chung, dễ hiểu và hiệu quả. Với sự trợ giúp của máy tính và phần mềm hiện đại, việc học và ứng dụng các công thức này càng trở nên dễ dàng và chính xác. Trong lập trình máy tính, các ứng dụng liên quan đến hình ảnh, âm thanh đều có những mối liên hệ mật thiết với lượng giác, đặc biệt là trong việc xử lý đồ họa và tối ưu không gian. Phép Đo Góc và Trục Xoay là hai khái niệm phổ biến trong không gian hai chiều và ba chiều, thường được sử dụng trong phát triển trò chơi và hiệu suất truyền thông đa phương tiện. 

Từ định lý cho đến ứng dụng thực tế, một tam giác vuông nhỏ bé cũng có thể là nguồn cảm hứng để sáng tạo và mở ra vô vàn hướng đi mới trong nghiên cứu và triển khai. Với sự phát triển của công nghệ, các khóa học trực tuyến và các công cụ học tập hiện đại giúp người học dễ dàng tiếp cận, nắm bắt và cập nhật kiến thức về tam giác vuông cũng như mở rộng ra các lĩnh vực liên quan. Bằng việc khám phá các định lý mở rộng, người học không chỉ xây dựng nền tảng vững chắc mà còn sẵn sàng tham gia vào các cuộc phiêu lưu tri thức mới. 

Ứng dụng thực tiễn của tam giác vuông trong cuộc sống

Sự đơn giản, các tính chất rõ ràng và các định lý mạnh mẽ (đặc biệt là Pythagoras và lượng giác) đã đưa tam giác vuông trở thành một trong những hình học được ứng dụng rộng rãi nhất trong nhiều lĩnh vực khác nhau. Hiểu rõ các tính chất của tam giác vuông là chìa khóa để áp dụng chúng một cách hiệu quả trong thực tế.

Xây dựng và kiến trúc

• Kiểm tra độ vuông góc: Các công nhân xây dựng thường sử dụng "quy tắc 3-4-5" để đảm bảo các góc tường hoặc nền móng là vuông vắn. Nếu đo được ba cạnh của một tam giác là 3 đơn vị, 4 đơn vị và 5 đơn vị, thì đó là một tam giác vuông (vì 3²+4²=9+16=25=5²). Nguyên tắc này là ứng dụng trực tiếp của Định lý Pythagoras.
• Thiết kế cấu trúc: Tam giác, đặc biệt là tam giác vuông, được sử dụng trong thiết kế giàn (trusses) cho mái nhà, cầu, tháp truyền hình vì sự ổn định và khả năng chịu lực tốt. Tính toán độ dài các thanh giàn và góc nối thường dùng Pythagoras và lượng giác.
• Đo đạc và lập bản đồ: Tam giác vuông được sử dụng trong kỹ thuật trắc địa và đo đạc để xác định khoảng cách và độ cao của các điểm trên mặt đất. Phương pháp "tam giác đạc" (triangulation), dù phức tạp hơn tam giác vuông đơn lẻ, vẫn dựa trên nguyên tắc cơ bản của việc xác định vị trí dựa trên các góc và cạnh của tam giác.

Kỹ thuật

• Thiết kế cơ khí: Phân tích lực, tính toán moment xoắn, thiết kế bánh răng, và các bộ phận máy móc thường xuyên sử dụng lượng giác để phân tích các thành phần lực theo phương vuông góc.
• Robotics: Để cánh tay robot di chuyển chính xác đến một điểm trong không gian, hệ thống điều khiển phải liên tục tính toán các góc quay của các khớp dựa trên vị trí mục tiêu và độ dài các đoạn nối. Đây là bài toán "động học ngược" (inverse kinematics) sử dụng rộng rãi lượng giác.
• Điện và điện tử: Phân tích mạch điện xoay chiều (AC) sử dụng biểu diễn vector và số phức, nơi các thành phần điện trở, dung kháng, cảm kháng thường được biểu diễn trên một "tam giác trở kháng" (impedance triangle) dựa trên nguyên tắc tam giác vuông.

Tạm kết

Hiểu biết và khám phá sâu về các tính chất của tam giác vuông không chỉ giúp người học nâng cao kỹ năng toán học mà còn mở ra nhiều hướng phát triển nghề nghiệp và sáng tạo mới. Nắm vững những kiến thức này là cơ hội để mở rộng khả năng ứng dụng và tận dụng tối đa tiềm năng của hình học trong đời sống và công việc hàng ngày.

Với những bạn học sinh, sinh viên hay giáo viên đang tìm kiếm công cụ hỗ trợ học toán trực quan, dễ thao tác và mang lại trải nghiệm học tập hiện đại – iPad chính là trợ thủ đắc lực. Từ việc vẽ hình tam giác vuông bằng Apple Pencil, ghi chú công thức nhanh chóng, đến sử dụng các ứng dụng học lượng giác, hình học động như GeoGebra, iPad giúp bạn hiểu sâu, nhớ lâu và học mọi lúc mọi nơi. Khám phá các dòng iPad học tập chất lượng tại FPT Shop – chính hãng 100%, trả góp 0%, nhiều ưu đãi dành riêng cho học sinh – sinh viên!

iPad

Xem thêm:

• Hướng dẫn cách tính diện tích hình tam giác và các dạng bài tập
• Tất tần tật về diện tích tam giác vuông