Đường trung tuyến là gì? Các tính chất quan trọng cần nắm và công thức tính

Đường trung tuyến là một khái niệm quan trọng trong hình học, thường được sử dụng trong việc chứng minh và giải toán. Trong bài viết này, FPT Shop sẽ giúp bạn hiểu rõ đường trung tuyến là gì và các tính chất quan trọng trong từng loại tam giác.

Đường trung tuyến là gì?

Đường trung tuyến là gì? Trong hình học, đường trung tuyến là một đoạn thẳng đặc biệt. Nó có thể được hiểu theo hai cách:

• Đối với một đoạn thẳng: Đường trung tuyến là bất kỳ đường thẳng nào đi qua điểm chính giữa của đoạn thẳng đó (gọi là trung điểm). Trung điểm chia đoạn thẳng thành hai phần bằng nhau.
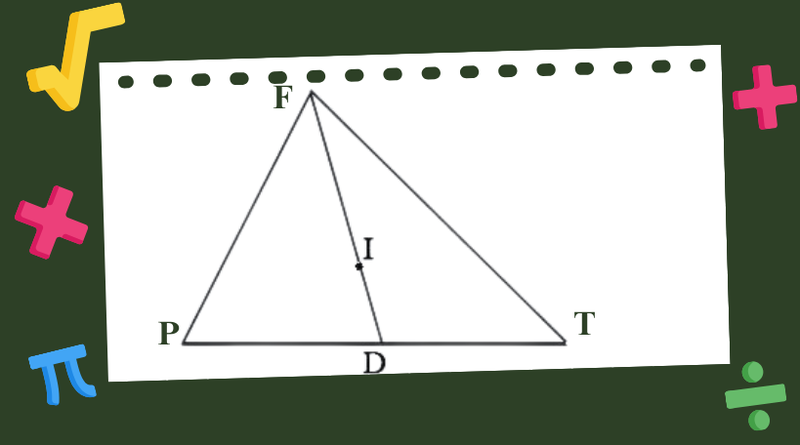
• Đối với một tam giác: Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện (cạnh nằm đối diện với đỉnh đó). Trong một tam giác, có ba đường trung tuyến, mỗi đường nối một đỉnh với trung điểm của cạnh đối diện.

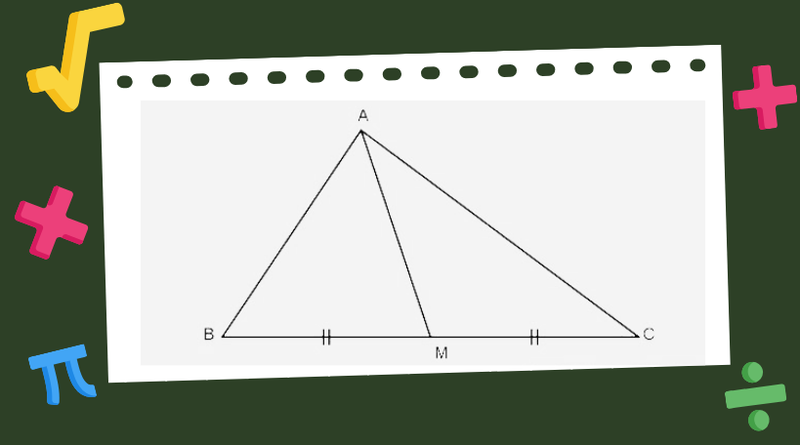
Để hiểu rõ hơn, hãy hình dung trung điểm là điểm nằm ngay chính giữa một đoạn thẳng, sao cho khoảng cách từ trung điểm đến hai đầu mút của đoạn thẳng là như nhau.

Trong tam giác, ba đường trung tuyến có một tính chất đặc biệt: chúng luôn cắt nhau tại một điểm duy nhất, gọi là trọng tâm của tam giác. Trọng tâm này có một số tính chất quan trọng, ví dụ như nó chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện.

Để việc tính toán trở nên thuận tiện và chính xác hơn, hãy sử dụng máy tính cầm tay! Đây là thiết bị tiện ích giúp bạn thực hiện phép toán nhanh chóng, từ những phép tính cơ bản đến nâng cao.

Tính chất đường trung tuyến cần nắm

Sau khi các bạn đã hiểu hơn về đường trung tuyến là gì, hãy cùng tìm hiểu thêm về tính chất đường trung tuyến trong các dạng tam giác!

Tính chất đường trung tuyến trong tam giác thường

Mỗi tam giác thường có ba đoạn trung tuyến. Mỗi đường trung tuyến là một đoạn thẳng nối từ một đỉnh của tam giác đến điểm chính giữa (trung điểm) của cạnh đối diện với đỉnh đó. Ba đường trung tuyến này luôn giao nhau tại một điểm duy nhất, gọi là trọng tâm của tam giác.

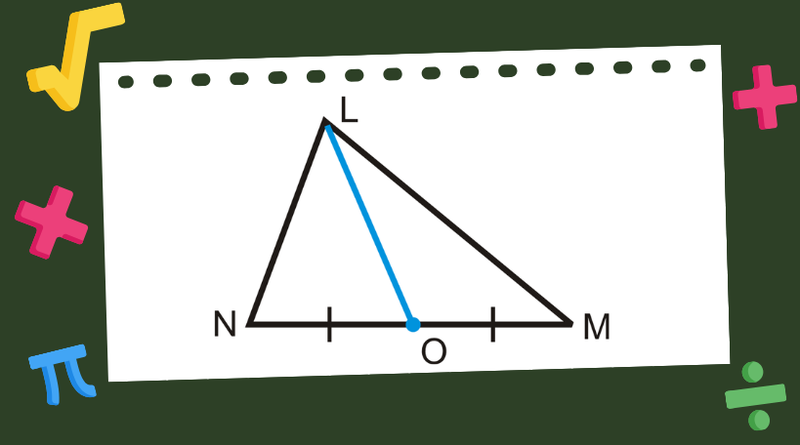
Trọng tâm chia mỗi đường trung tuyến thành hai đoạn có độ dài theo tỉ lệ 2:1, nghĩa là đoạn từ đỉnh đến trọng tâm dài gấp đôi đoạn từ trọng tâm đến trung điểm của cạnh đối diện. Khi nối trọng tâm với ba đỉnh của tam giác, ta được ba đoạn thẳng nằm hoàn toàn bên trong tam giác.

Tính chất của đường trung tuyến trong tam giác vuông

Trong tam giác vuông, đường trung tuyến xuất phát từ đỉnh góc vuông và đi đến trung điểm của cạnh huyền (cạnh dài nhất) có một tính chất đặc biệt: độ dài của nó bằng một nửa độ dài cạnh huyền. Điều này có thể được chứng minh dễ dàng bằng cách chia tam giác vuông thành hai tam giác nhỏ bằng nhau. Các đường trung tuyến cũng giao nhau tại trọng tâm.

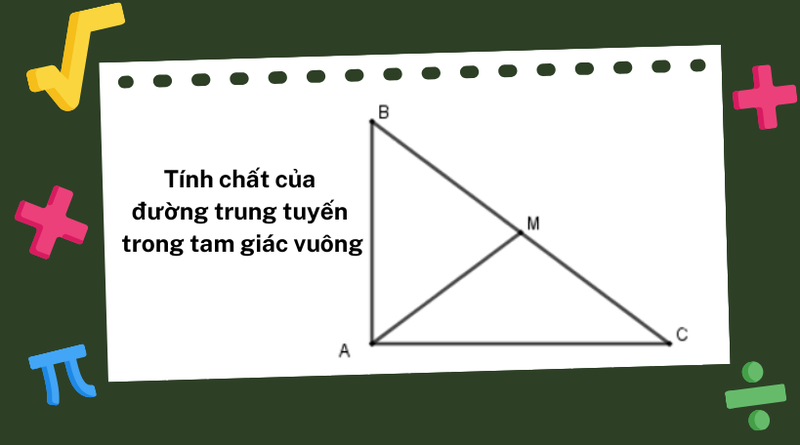
Ví dụ minh họa:

Xét tam giác ABC vuông tại A, với AD là đường trung tuyến ứng với cạnh huyền BC. Khi đó:

• AD = 1/2 BC = DB = DC

Ngược lại: Nếu trong tam giác ABC, đường trung tuyến AD thỏa mãn điều kiện AD = 1/2 BC, thì tam giác ABC là tam giác vuông tại đỉnh A.

Tính chất của đường trung tuyến trong tam giác cân

Xét tam giác ABC cân tại đỉnh A và AD là đường trung tuyến kẻ từ đỉnh A xuống cạnh đáy BC. Khi đó, ta có những tính chất sau:

• AD vuông góc với BC: Đường trung tuyến AD không chỉ chia cạnh đáy BC thành hai phần bằng nhau, mà còn vuông góc với cạnh đáy đó. Nói cách khác, AD là đường cao của tam giác cân ABC.
• ΔADB = ΔADC: Đường trung tuyến AD chia tam giác cân ABC thành hai tam giác nhỏ, ΔADB và ΔADC, hoàn toàn bằng nhau.

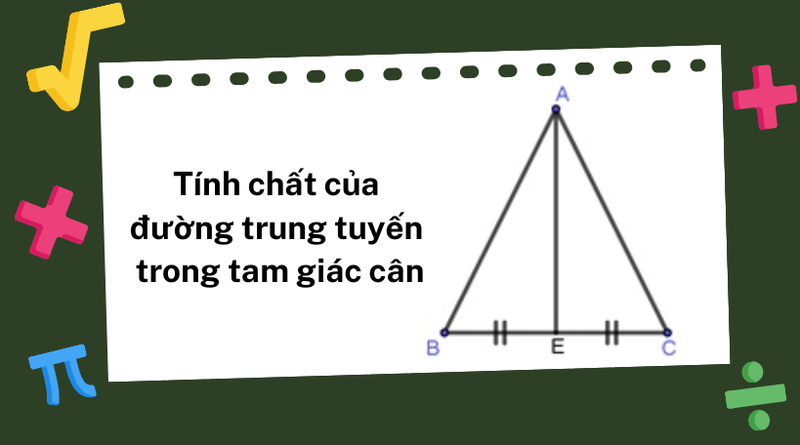
Trong tam giác cân, đường trung tuyến kẻ từ đỉnh cân đến cạnh đáy vừa là đường trung tuyến, vừa là đường cao, vừa là đường phân giác của góc ở đỉnh. Nó chia tam giác cân thành hai tam giác vuông bằng nhau. Ba đường trung tuyến cắt nhau tại trọng tâm của tam giác.

Công thức tính độ dài đường trung tuyến của tam giác

Có một công thức đặc biệt giúp chúng ta tính độ dài đường trung tuyến trong một tam giác, gọi là định lý Apollonius. Công thức này khá hữu ích vì nó chỉ cần biết độ dài các cạnh của tam giác.

Hãy tưởng tượng bạn có một tam giác tên là ABC, với các cạnh có độ dài lần lượt là a, b và c. Bây giờ, bạn muốn tìm độ dài đường trung tuyến xuất phát từ đỉnh A, nối đến trung điểm của cạnh BC (gọi điểm này là M). Định lý Apollonius cho chúng ta công thức sau:

• Độ dài AM² = (b² + c²) / 2 - a²/4.

Với công thức này, bạn có thể tính được độ dài đường trung tuyến AM một cách dễ dàng. Tương tự, bạn có thể áp dụng công thức này để tính độ dài các đường trung tuyến khác (từ đỉnh B và đỉnh C) bằng cách thay đổi vai trò của các cạnh a, b và c cho phù hợp.

Lưu ý: Công thức Apollonius này luôn đúng với mọi tam giác. Điều quan trọng là bạn phải xác định chính xác cạnh nào là 'a' (cạnh đối diện với đỉnh mà đường trung tuyến xuất phát từ đó) và các cạnh 'b' và 'c' là hai cạnh còn lại.

Nếu bạn không biết độ dài các cạnh của tam giác, bạn cần sử dụng các phương pháp khác để tính độ dài đường trung tuyến, ví dụ như sử dụng các công thức liên quan đến góc và cạnh trong tam giác.

Lời kết

Qua bài viết trên, FPT Shop đã giải đáp thắc mắc: ”Trung tuyến là gì?”, cũng như tính chất trung tuyến của từng loại tam giác. Hy vọng sau khi đọc xong bài viết, bạn sẽ có thêm nhiều kiến thức toán học hữu ích nhé.

Nếu bạn cần một chiếc smartphone chất lượng, giá phải chăng để hỗ trợ học tập, tìm kiếm các công thức khác nhau nhanh chóng, có thể chọn ngay điện thoại OPPO giá tốt tại FPT Shop.

Tham khảo ngay tại đây: Điện thoại OPPO

Xem thêm

• Thế nào là tính chất trọng tâm tam giác, tổng hợp công thức tính và bài tập vận dụng
• Cách tính diện tích tam giác: Tổng hợp các công thức từ cơ bản đến nâng cao