Trọng tâm tam giác là gì? Tìm hiểu tính chất, công thức tính và bài tập vận dụng

Việc hiểu rõ tính chất trọng tâm tam giác giúp người học vận dụng để giải các bài tập hình học chính xác hơn. Đồng thời, điều này còn giúp các bạn xây dựng kế hoạch ôn luyện hiệu quả để đạt kết quả tốt trong các kỳ kiểm tra.

Trong bài viết về trọng tâm tam giác dưới đây, FPT Shop sẽ chia thành các phần chính: Tổng quan lý thuyết, các tính chất và bài tập vận dụng có hướng dẫn chi tiết, giúp người học dễ tiếp thu và ghi nhớ kiến thức nhanh chóng

Trọng tâm là gì?

Trọng tâm của một vật là điểm đặc biệt mà nếu bạn đặt một điểm tựa (như đầu ngón tay hoặc một cái trụ) ngay tại đó, vật sẽ giữ được thăng bằng và không bị đổ.

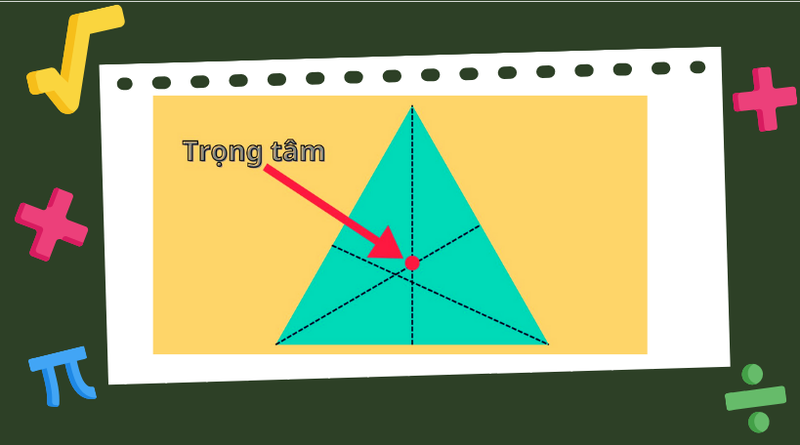
Chúng ta thường nghe đến "trọng tâm" trong cuộc sống hằng ngày, nó có nghĩa là điểm chính giữa, điểm quan trọng nhất của một vật thể hoặc một vấn đề nào đó. Trong toán học, khái niệm trọng tâm được sử dụng nhiều trong hình học. Ví dụ, chúng ta có thể tìm trọng tâm của một tam giác, hình chữ nhật, hoặc hình tứ giác – đó là điểm "cân bằng" của những hình này.

Trọng tâm tam giác là gì?

Trong một tam giác, có một điểm đặc biệt gọi là trọng tâm. Để tìm được trọng tâm này, chúng ta cần biết đường trung tuyến là gì. Đường trung tuyến là một đoạn thẳng nối từ một góc của tam giác đến trung điểm của cạnh đối diện với góc đó.

Ví dụ, chúng ta có tam giác ABC. Hãy vẽ một đường thẳng từ góc A đến trung điểm của cạnh BC (gọi điểm này là M). Tương tự, vẽ đường thẳng từ góc B đến điểm chính giữa của cạnh AC (gọi điểm này là N), và từ góc C đến điểm trung điểm của cạnh AB (gọi điểm này là P). Chúng ta có ba đường trung tuyến: AM, BN và CP.

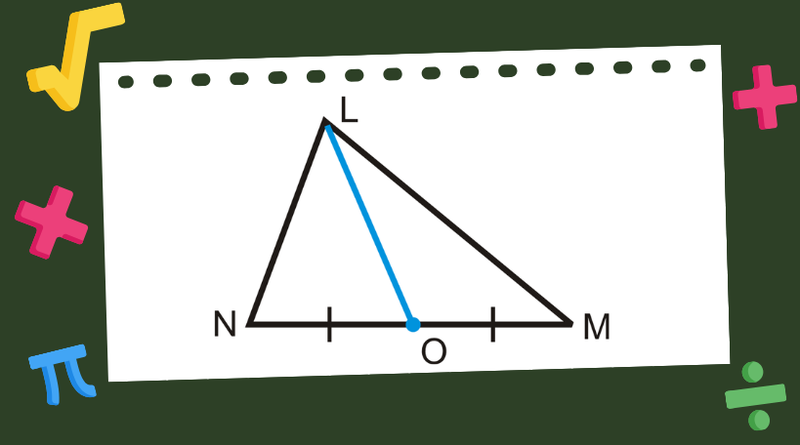
Bạn sẽ thấy rằng ba đường trung tuyến này cắt nhau tại một điểm duy nhất. Điểm này chính là trọng tâm của tam giác ABC. Chúng ta thường ký hiệu trọng tâm là G. Như vậy, trọng tâm là điểm giao nhau của ba đường trung tuyến trong một tam giác.

Tính chất trọng tâm tam giác

Điểm đặc biệt của trọng tâm tam giác là nó nằm trên mỗi đường trung tuyến và chia đường trung tuyến đó theo một tỉ lệ nhất định. Cụ thể, khoảng cách từ trọng tâm đến mỗi đỉnh của tam giác bằng 2/3 độ dài của đường trung tuyến xuất phát từ đỉnh đó.

Ví dụ, trong tam giác ABC, nếu G là trọng tâm và AM, BN, CP là ba đường trung tuyến, thì:

• Khoảng cách từ G đến đỉnh A (GA) bằng 2/3 độ dài của AM: GA = (2/3)AM.
• Khoảng cách từ G đến đỉnh B (GB) bằng 2/3 độ dài của BN: GB = (2/3)BN.
• Khoảng cách từ G đến đỉnh C (GC) bằng 2/3 độ dài của CP: GC = (2/3)CP.

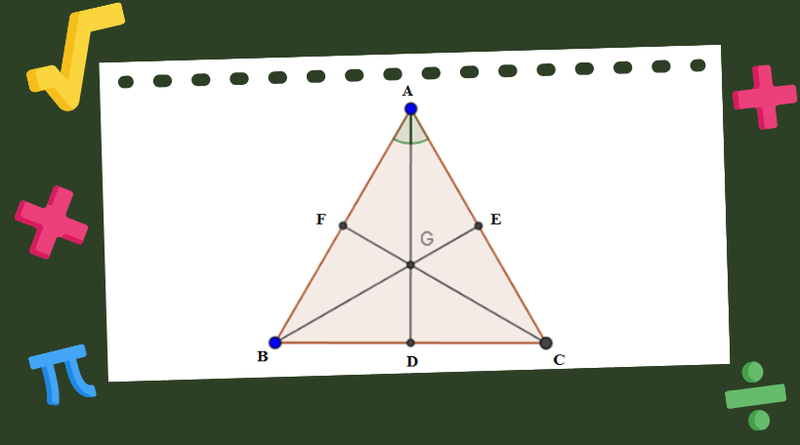
Chúng ta có thể biểu diễn mối quan hệ này như sau:

Đối với đường trung tuyến AM:

• AM dài gấp ba lần đoạn GM: AM = 3GM
• AM dài gấp 1.5 lần đoạn AG: AM = (3/2)AG (hay AG = (2/3)AM, như đã nói ở trên)
• AG dài gấp đôi đoạn GM: AG = 2GM
• GM bằng một nửa đoạn AG: GM = (1/2)AG

Tương tự với đường trung tuyến BN: BN = 3GN; BN = (3/2)BG; BG = 2GN; GN = (1/2)BG và với đường trung tuyến CP: CP = 3GP; CP = (3/2)CG; CG = 2GP; GP = (1/2)CG

• Lưu ý: AG, BG, CG, GM, GN, GP là độ dài của các đoạn thẳng.

Với mỗi loại tam giác đặc biệt, vị trí và tính chất của trọng tâm sẽ có những đặc điểm riêng.

Tính chất trọng tâm tam giác vuông

Nếu chúng ta có tam giác MNP vuông tại M, và O là trọng tâm của nó, thì đường trung tuyến MD (xuất phát từ góc vuông M) có một đặc điểm đặc biệt: nó bằng một nửa cạnh huyền PN (cạnh đối diện với góc vuông). Điều này có nghĩa là MD = 1/2 PN = DP = DN.

Tính chất trọng tâm tam giác cân

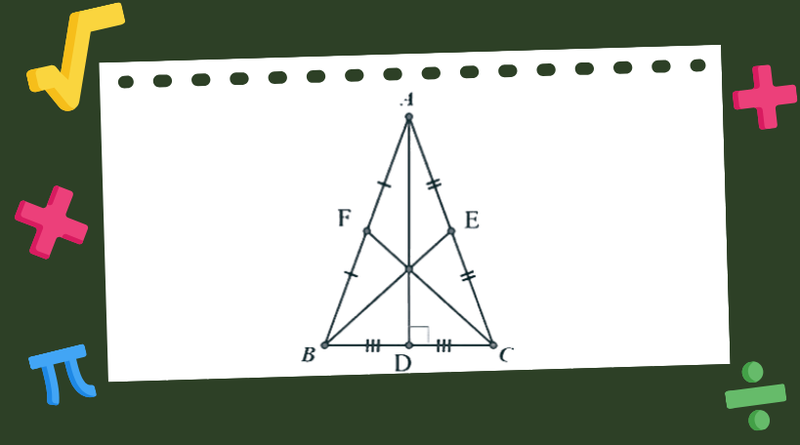
Trong tam giác cân ABC (cân tại A), nếu G là trọng tâm, thì đường trung tuyến AG không chỉ là đường trung tuyến thông thường mà còn đồng thời là đường cao (vuông góc với cạnh đáy BC) và đường phân giác (chia góc A thành hai góc bằng nhau).

Dựa vào tính chất trên, ta có các kết quả sau:

• Góc BAD bằng góc CAD (AD là đường phân giác).
• Đường trung tuyến AD vuông góc với cạnh đáy BC (AD là đường cao).

Để quá trình tính toán trở nên dễ dàng và chính xác hơn, hãy sử dụng máy tính cầm tay! Đây là công cụ hữu ích giúp bạn giải toán nhanh chóng, từ những phép tính đơn giản đến phức tạp.

Tính chất trọng tâm tam giác vuông cân

Nếu tam giác ABC vừa vuông, vừa cân tại A và I là trọng tâm, thì đường trung tuyến AM (xuất phát từ góc vuông cân A) cũng là đường trung trực và đường cao. Điều này có nghĩa là AM vuông góc với BC.

Ngoài ra, vì tam giác vuông cân nên AB = AC, dẫn đến BP = CN và BN = AN = CP = AP. (Ở đây, P và N là trung điểm của AB và AC tương ứng).

Tính chất trọng tâm tam giác đều

Trong tam giác đều ABC, nếu G là trọng tâm, thì G không chỉ là trọng tâm mà còn là giao điểm của ba đường cao, ba đường phân giác, tâm của đường tròn ngoại tiếp và tâm của đường tròn nội tiếp tam giác. Nói cách khác, tất cả các điểm đặc biệt này đều trùng nhau tại G.

Cách xác định trọng tâm tam giác

Chúng ta có hai cách đơn giản để tìm trọng tâm của một tam giác ABC:

Cách 1: Tìm giao điểm của ba đường trung tuyến (Đây là cách thường dùng nhất)

• Bước 1: Vẽ tam giác ABC trên giấy. Sau đó, tìm điểm chính giữa của mỗi cạnh (AB, BC, CA). Gọi các điểm này lần lượt là D, E, F.
• Bước 2: Vẽ một đường thẳng nối từ đỉnh A đến điểm E (điểm chính giữa của cạnh BC). Tương tự, vẽ đường thẳng từ đỉnh B đến điểm F (điểm chính giữa của cạnh AC), và từ đỉnh C đến điểm D (điểm chính giữa của cạnh AB).
• Bước 3: Ba đường thẳng vừa vẽ (AE, BF, CD) sẽ cắt nhau tại một điểm. Điểm này chính là trọng tâm của tam giác ABC, thường được ký hiệu là G.

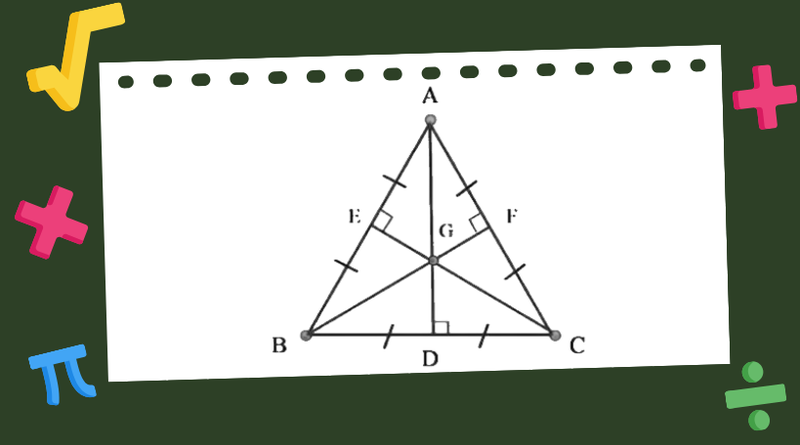
Cách 2: Sử dụng tỉ lệ 2/3 trên đường trung tuyến

• Bước 1: Vẽ tam giác ABC. Sau đó, tìm điểm chính giữa của cạnh BC và gọi điểm này là M.
• Bước 2: Vẽ đường thẳng nối từ đỉnh A đến điểm M.
• Bước 3: Đo độ dài đoạn thẳng AM. Sau đó, tìm một điểm S trên đoạn AM sao cho khoảng cách từ A đến S (AS) bằng 2/3 độ dài của AM. Điểm S này chính là trọng tâm của tam giác ABC. (Bạn có thể dùng thước để đo và chia đoạn AM thành ba phần bằng nhau, sau đó lấy hai phần tính từ điểm A).

Một số bài tập và lời giải

Bài tập 1: Tam giác ABC có trung tuyến AD dài 12 cm và trọng tâm I. Tính độ dài đoạn AI?

Lời giải

Ta biết rằng I là trọng tâm của tam giác FPT và FD là đường trung tuyến, do đó FI= (2/3) FD (theo tính chất của ba đường trung tuyến trong tam giác).

Vậy: FI = (2/3) × 12 = 8 cm. Như vậy, đoạn FI có độ dài 8 cm.

Bài tập 2: Cho tam giác FPT vuông tại F với G là trọng tâm. Chứng minh rằng hai tam giác FIP và FIT là tam giác cân.

Lời giải

Xét tam giác FPT vuông góc tại F với điểm G là trọng tâm. Do FI là đường trung tuyến xuất phát từ đỉnh góc vuông, vì vậy ta có: FI = 1/2 PT = PI = IT.

Suy ra, tam giác FIP và tam giác FIT lần lượt cân tại I.

Bài tập 3: Cho tam giác ABC vuông cân tại A, với G là trọng tâm. Gọi M là giao điểm của BG và AC, N là giao điểm của CG và AB. Chứng minh rằng:

a. BM=CN

b. BN=AN=CM=AM

Lời giải

Xét tam giác ABC vuông cân tại A với G là trọng tâm. Theo tính chất của đường trung trực trong tam giác cân, AG vừa là đường trung trực, vừa là đường trung tuyến và đường cao của tam giác này.

Do đó, AG vuông góc với BC.

Ngoài ra, ta có: AB=AC (vì tam giác ABC là tam giác cân tại A).

Từ đó, ta suy ra được:

• BM=CN
• BN=AN=CM=AM

Lời kết

Như vậy, FPT Shop đã cùng bạn tìm hiểu trọng tâm tam giác, cũng như tính chất của từng loại tam giác. Hy vọng sau khi đọc xong bài viết, bạn sẽ có thêm nhiều kiến thức toán học hữu ích nhé.

Nếu bạn đang tìm kiếm một chiếc laptop mới để hỗ trợ việc học tập, nghiên cứu và tìm hiểu thêm về các chủ đề thú vị như toán học, đừng quên ghé thăm FPT Shop. Tại đây, bạn sẽ tìm thấy những chiếc laptop với hiệu năng mạnh mẽ, màn hình sắc nét và nhiều tính năng hữu ích, giúp bạn hoàn thành tốt mọi công việc học tập.

• Laptop

Xem thêm

• Công thức tính đường cao tam giác cân đơn giản, dễ hiểu mà bạn có thể áp dụng hiệu quả
• Cách tính diện tích tam giác: Tổng hợp các công thức từ cơ bản đến nâng cao