Cách tính diện tích tam giác: Tổng hợp các công thức từ cơ bản đến nâng cao

Bài viết này sẽ là bí kíp dẫn dắt bạn khám phá mọi ngóc ngách kiến thức về cách tính diện tích tam giác, từ những công thức cơ bản nhất đến những trường hợp đặc biệt, kèm theo ví dụ minh họa sinh động và bài tập ứng dụng phong phú, giúp bạn tự tin chinh phục mọi bài toán liên quan đến diện tích tam giác.

Công thức chung tính diện tích tam giác

Dù tam giác có hình dạng, kích thước như thế nào, công thức chung để tính diện tích luôn là:

S = (a x h) / 2

Trong đó:

• S: Diện tích tam giác, đại diện cho phần không gian mà tam giác đó chiếm giữ.
• a: Độ dài đáy của tam giác. Đáy có thể là bất kỳ cạnh nào của tam giác, tùy thuộc vào cách bạn chọn.
• h: Chiều cao tương ứng với đáy a. Đây là đoạn thẳng vuông góc kẻ từ đỉnh đối diện với đáy.

Lưu ý quan trọng:

• Việc xác định đúng đáy và chiều cao tương ứng là bước then chốt để áp dụng chính xác công thức.
• Đơn vị đo diện tích thường là cm², m², km²,... tùy thuộc vào đơn vị đo độ dài của đáy và chiều cao.

Cách tính diện tích tam giác trong những trường hợp đặc biệt

Bên cạnh công thức chung, một số loại tam giác đặc biệt cho phép chúng ta áp dụng những công thức riêng giúp việc tính toán trở nên nhanh chóng và thuận tiện hơn.

Tính diện tích tam giác vuông

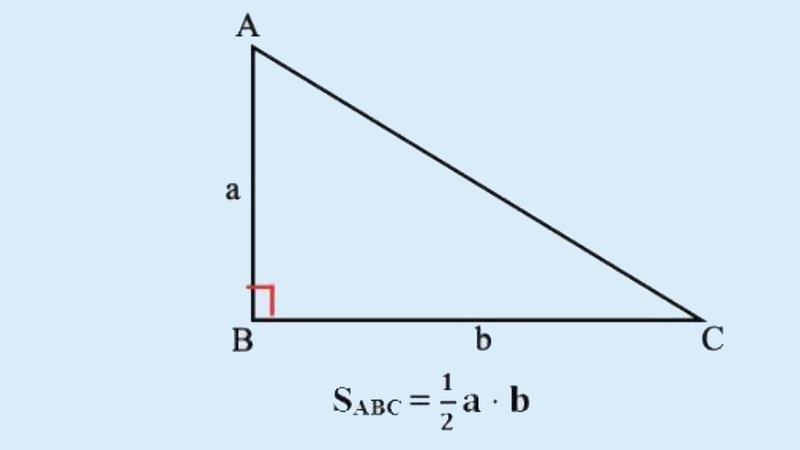
Với tam giác vuông, hai cạnh góc vuông chính là đáy và chiều cao tương ứng của nhau. Do đó, ta có công thức đơn giản hơn:

S = (1/2) * a * b (với a, b là độ dài hai cạnh góc vuông)

Tính diện tích tam giác đều

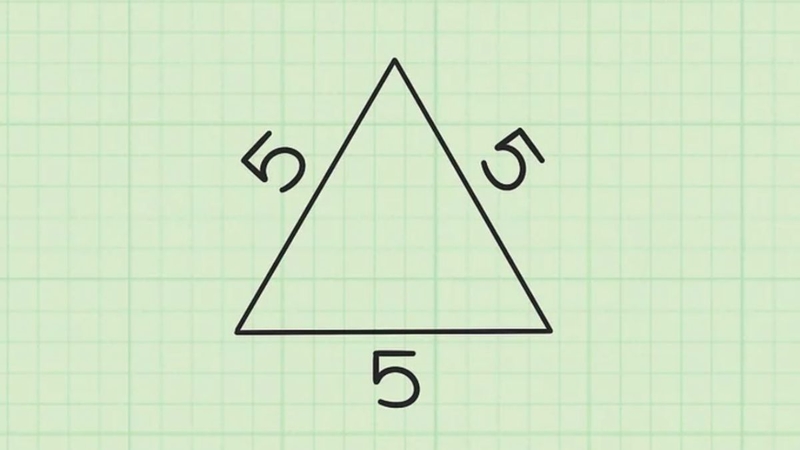
Tam giác đều có ba cạnh bằng nhau và ba góc bằng 60 độ. Để tính diện tích tam giác đều, ta sử dụng công thức:

S = (a² * √3) / 4 (với a là độ dài cạnh của tam giác đều)

Tính diện tích tam giác cân

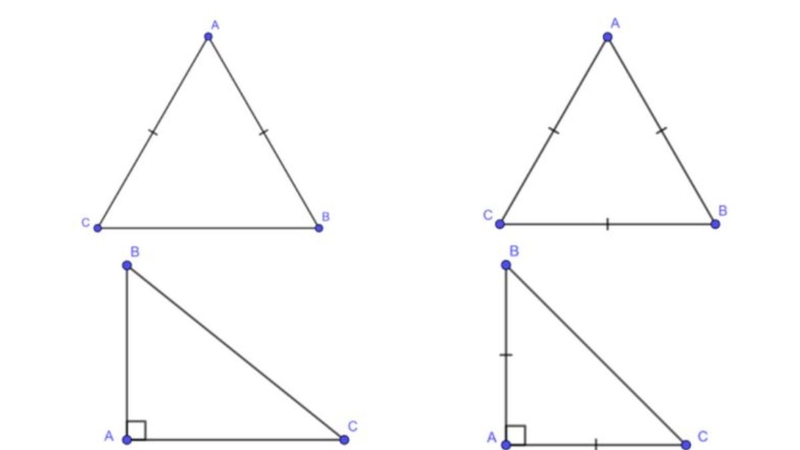
Tam giác cân có hai cạnh bên bằng nhau. Ta có thể áp dụng công thức chung để tính diện tích tam giác cân. Ngoài ra, nếu biết độ dài hai cạnh bên và góc ở đỉnh, ta có thể sử dụng công thức:

S = (1/2) * b * c * sin(A) (với b, c là độ dài hai cạnh bên, A là góc ở đỉnh)

Tính diện tích tam giác khi biết 3 cạnh

Khi biết độ dài ba cạnh của tam giác, ta có thể áp dụng công thức Heron để tính diện tích:

• p = (a + b + c) / 2 (với a, b, c là độ dài ba cạnh tam giác, p là nửa chu vi)
• S = √[p(p - a)(p - b)(p - c)]

Tính diện tích tam giác khi biết 2 cạnh và góc xen giữa

Nếu biết độ dài hai cạnh và góc xen giữa của tam giác, ta có công thức:

S = (1/2) * a * b * sin(C) (với a, b là độ dài hai cạnh, C là góc xen giữa)

Thực hành với bài tập

Để củng cố kiến thức và rèn luyện kỹ năng cách tính diện tích tam giác, hãy cùng thử sức với một số bài tập ứng dụng sau đây:

Bài tập 1: Một mảnh đất hình tam giác vuông có hai cạnh góc vuông lần lượt là 12m và 16m. Tính diện tích mảnh vườn này.

Bài tập 2: Một tấm biển quảng cáo hình tam giác đều cạnh 2m. Tính diện tích tấm biển.

Bài tập 3: Một cánh buồm hình tam giác cân có cạnh đáy 4m, hai cạnh bên 5m. Tính diện tích cánh buồm.

Bài tập 4: Một thửa ruộng hình tam giác có độ dài ba cạnh lần lượt là 20m, 25m và 30m. Tính diện tích thửa ruộng.

Bài tập 5: Một miếng đất hình tam giác có hai cạnh dài 10m và 15m, góc xen giữa hai cạnh này là 45 độ. Tính diện tích miếng đất.

(Hãy thử tự giải các bài tập này trước khi xem đáp án ở cuối bài viết nhé!)

Ứng dụng của cách tính diện tích tam giác trong đời sống

Cách tính diện tích tam giác tưởng chừng như khô khan và chỉ tồn tại trên trang giấy lại có mặt trong rất nhiều khía cạnh của cuộc sống. Từ những công trình kiến trúc đồ sộ đến những vật dụng nhỏ bé trong gia đình, việc tính toán diện tích tam giác đều đóng vai trò quan trọng, giúp chúng ta giải quyết nhiều vấn đề thực tiễn.

Ứng dụng trong xây dựng

Trong lĩnh vực xây dựng, việc tính toán diện tích tam giác là điều không thể thiếu. Các kiến trúc sư và kỹ sư thường xuyên phải làm việc với các hình tam giác trong thiết kế mái nhà, cửa sổ, tường, và nhiều chi tiết khác.

Ví dụ, để thiết kế một mái nhà hình tam giác, kiến trúc sư cần tính toán chính xác diện tích mái để lựa chọn loại vật liệu phù hợp, đảm bảo độ bền vững và tính thẩm mỹ cho công trình. Việc tính toán diện tích tam giác cũng giúp dự trù lượng vật liệu cần thiết, từ đó tối ưu hóa chi phí xây dựng.

Không chỉ vậy, trong thiết kế các công trình kiến trúc phức tạp, việc chia nhỏ các hình dạng thành các tam giác giúp đơn giản hóa việc tính toán diện tích mặt bằng, lập kế hoạch thi công, và đảm bảo sự chính xác cho toàn bộ dự án.

Ứng dụng trong thiết kế

Tính toán diện tích tam giác cũng là một công cụ hữu ích trong lĩnh vực thiết kế. Các nhà thiết kế đồ họa thường xuyên sử dụng hình tam giác để tạo ra các logo, banner, và các ấn phẩm quảng cáo ấn tượng.

Việc tính toán diện tích các hình tam giác này giúp họ phân chia bố cục một cách hợp lý, tạo sự cân đối và hài hòa cho sản phẩm. Trong thiết kế web, hình tam giác cũng được sử dụng để tạo ra các nút bấm, biểu tượng, và các yếu tố đồ họa khác. Việc tính toán diện tích giúp đảm bảo các yếu tố này được hiển thị đúng kích thước và tỷ lệ trên các thiết bị khác nhau.

Ứng dụng trong đo đạc

Trong lĩnh vực đo đạc, việc tính toán diện tích tam giác có vai trò then chốt trong việc quản lý đất đai và tài nguyên. Các kỹ sư trắc địa sử dụng các công cụ và phương pháp đo đạc hiện đại để xác định chính xác diện tích các khu đất, thửa ruộng, và các loại hình bất động sản khác.

Thông tin về diện tích là cơ sở pháp lý quan trọng để phân chia, giao dịch, và quản lý đất đai một cách hiệu quả. Ngoài ra, việc tính toán diện tích tam giác cũng được ứng dụng trong việc xác định diện tích rừng, diện tích mặt nước, hỗ trợ công tác quản lý tài nguyên môi trường, bảo vệ đa dạng sinh học.

Ứng dụng trong cuộc sống hàng ngày

Ngay cả trong những hoạt động thường ngày, kiến thức về diện tích tam giác cũng có thể giúp ích cho chúng ta. Khi may vá, bạn có thể ứng dụng công thức tính diện tích tam giác để ước lượng lượng vải cần thiết cho các chi tiết hình tam giác trên quần áo.

Tương tự, khi gói quà, việc tính toán diện tích giúp bạn lựa chọn kích thước giấy gói phù hợp, tránh lãng phí. Trong gia đình, bạn cũng có thể ước lượng diện tích của các vật dụng hình tam giác như khăn trải bàn, gương, tranh ảnh,... để sắp xếp và bố trí không gian sống một cách hài hòa và tiện lợi.

Đáp án bài tập

• Bài tập 1: 96 m²
• Bài tập 2: √3 m²
• Bài tập 3: 12 m²
• Bài tập 4: Khoảng 290.47 m²
• Bài tập 5: 35.36 m²

Tạm kết

Bài viết đã cung cấp cho bạn một cái nhìn toàn diện về cách tính diện tích tam giác, từ những kiến thức nền tảng đến những ứng dụng đa dạng. Hy vọng rằng, bạn đã trang bị cho mình "vũ khí" tự tin để giải quyết mọi bài toán liên quan đến diện tích tam giác, đồng thời nhận thức được vai trò quan trọng của kiến thức toán học trong cuộc sống.

Để hỗ trợ việc học tập, làm việc hiệu quả hơn, bên cạnh nắm rõ các công thức toán học, nguyên lý… thì việc sở hữu một chiếc laptop chắc chắn cũng sẽ cực kỳ hữu ích. Bạn hãy tham khảo ngay các sản phẩm laptop đang có mặt tại FPT Shop. Chúng tôi cam kết các sản phẩm tại đây luôn có mức giá hợp lý, nhiều khuyến mãi hấp dẫn cũng như chính sách bảo hành rõ ràng.

• Laptop giá tốt

Xem thêm:

• Bật mí cho bạn các cách tính đạo hàm nhanh chóng và chính xác trong toán học
• 6 ứng dụng toán học tốt và dễ dùng nhất cho học sinh cấp 1