Dấu hiệu nhận biết hình chữ nhật: Kiến thức nền tảng trong toán hình học ở chương trình phổ thông

Trong chương trình toán học phổ thông, hình chữ nhật là kiến thức nền tảng để học tốt các phần về hình học phẳng và hình học không gian. Việc nắm vững dấu hiệu nhận biết hình chữ nhật không chỉ giúp giải nhanh bài tập mà còn giúp rèn luyện tư duy logic. Cùng tìm hiểu chi tiết về khái niệm, đặc điểm và cách nhận biết hình chữ nhật chính xác nhất. 

Khái niệm và đặc điểm cơ bản của hình chữ nhật

Trước khi tìm hiểu dấu hiệu nhận biết hình chữ nhật, ta cần hiểu khái niệm cơ bản của loại hình này.

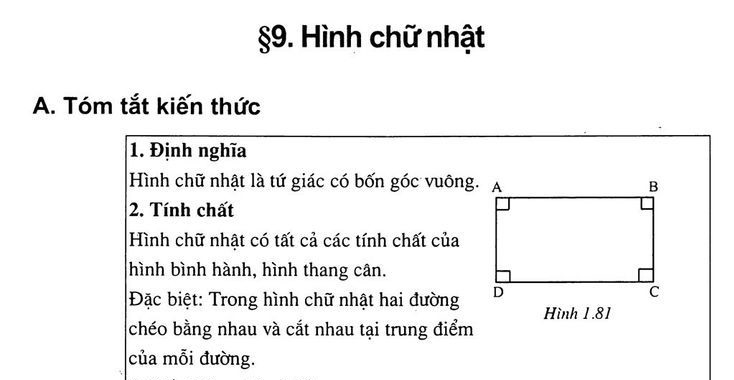
Hình chữ nhật là tứ giác có bốn góc vuông, nghĩa là mỗi góc trong đều bằng 90 độ. Đây là một trường hợp đặc biệt của hình bình hành, vì ngoài việc có hai cặp cạnh đối song song và bằng nhau, hình chữ nhật còn có thêm tính chất đặc trưng là các góc vuông.

Đặc điểm của hình chữ nhật:

• Có hai cặp cạnh đối song song và bằng nhau.
• Bốn góc vuông, mỗi góc 90°.
• Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

Những đặc điểm này giúp hình chữ nhật dễ nhận biết trong hình học cũng như trong các vật thể xung quanh chúng ta, từ màn hình điện thoại, cửa sổ đến tấm bảng học.

Dấu hiệu nhận biết hình chữ nhật

Để chứng minh hoặc nhận biết một tứ giác là hình chữ nhật, ta có thể dựa vào các dấu hiệu hình học sau đây. Đây là những quy tắc được dạy trong chương trình Toán lớp 8 – 9, giúp học sinh xác định nhanh hình dạng của tứ giác dựa trên quan hệ cạnh, góc và đường chéo.

Dấu hiệu 1: Hình bình hành có một góc vuông

Nếu một tứ giác là hình bình hành và có một góc vuông, thì tứ giác đó là hình chữ nhật.

Giải thích: Hình bình hành có các cạnh đối song song, nếu một góc vuông thì ba góc còn lại cũng vuông (vì tổng bốn góc bằng 360°). Do đó, tứ giác có bốn góc vuông → là hình chữ nhật.

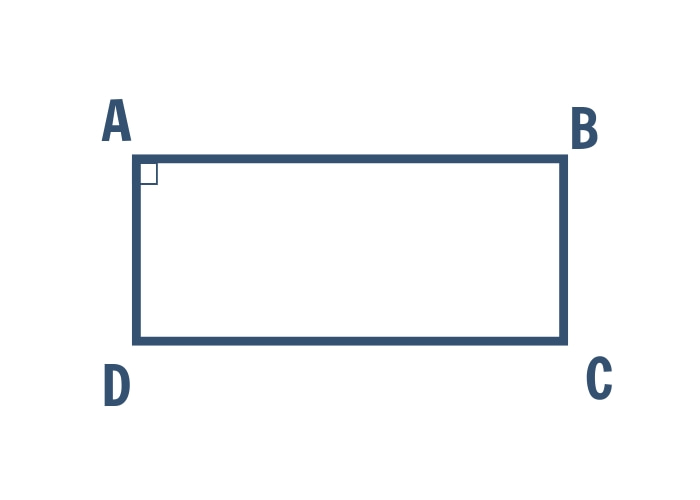
Ví dụ: Cho hình bình hành ABCD có góc A = 90°, chứng minh ABCD là hình chữ nhật.

→ Vì ABCD là hình bình hành và có một góc vuông, nên theo dấu hiệu trên, ABCD là hình chữ nhật.

Dấu hiệu 2: Hình bình hành có hai đường chéo bằng nhau

Nếu một hình bình hành có hai đường chéo bằng nhau, thì đó là hình chữ nhật.

Giải thích: Trong hình bình hành, hai đường chéo thường không bằng nhau (trừ khi có tính chất đặc biệt). Khi hai đường chéo bằng nhau, hình đã có sự đối xứng về kích thước, tạo thành các góc vuông tại đỉnh.

Ví dụ:

Hình bình hành ABCD có AC = BD.

→ Theo dấu hiệu, ABCD là hình chữ nhật.

Dấu hiệu 3: Tứ giác có ba góc vuông

Nếu một tứ giác có ba góc vuông, thì góc còn lại tự động là góc vuông, và tứ giác đó là hình chữ nhật.

Giải thích: Tổng bốn góc của tứ giác luôn bằng 360°. Nếu ba góc đã là 90°, thì góc thứ tư chắc chắn cũng là 90°.

Ví dụ: Tứ giác MNPQ có ba góc vuông tại M, N, P → Suy ra góc Q = 90° → MNPQ là hình chữ nhật.

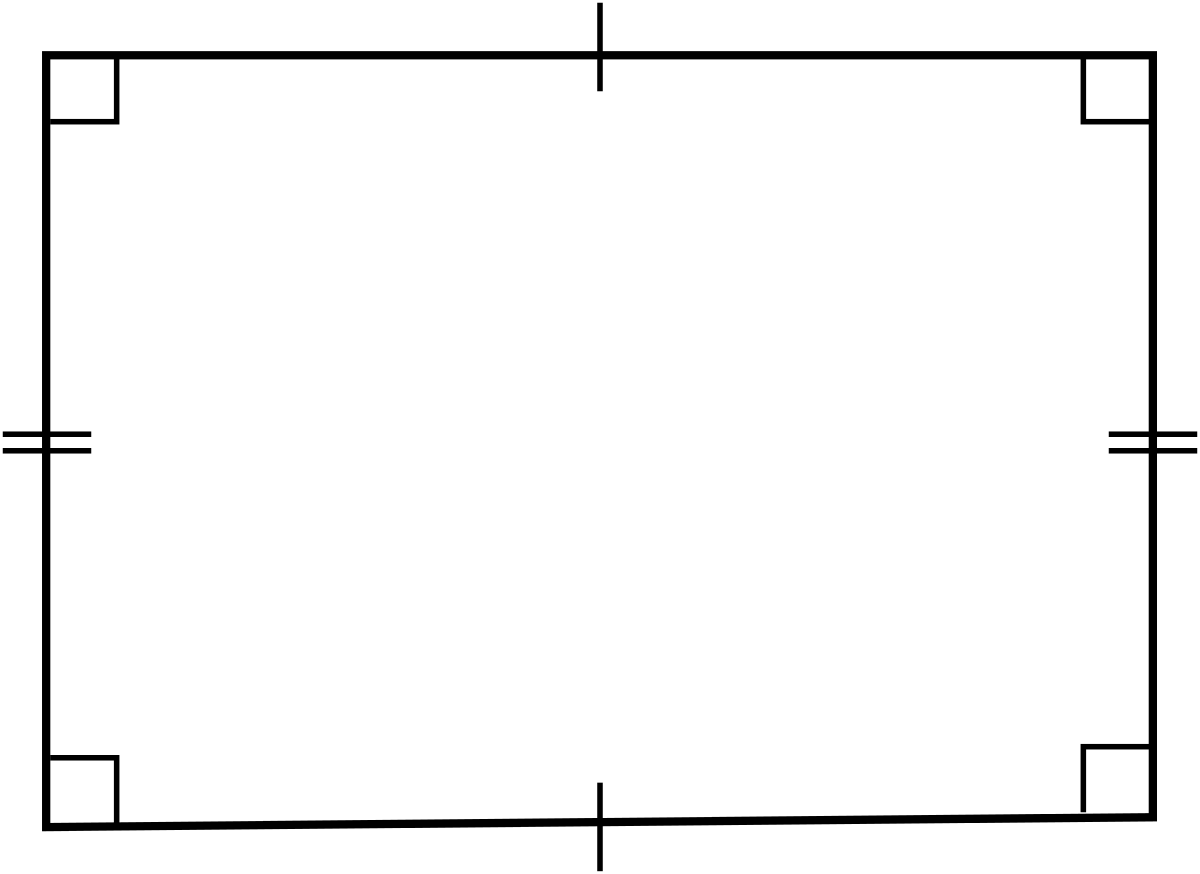
Dấu hiệu 4: Hình thang cân có hai đường chéo bằng nhau

Nếu một hình thang cân có hai đường chéo bằng nhau, thì đó cũng là hình chữ nhật.

Giải thích: Trong hình thang cân, hai cạnh bên bằng nhau, hai góc ở đáy bằng nhau. Khi hai đường chéo cũng bằng nhau, hình thang trở nên đối xứng hoàn toàn, tạo thành bốn góc vuông.

Ví dụ: Hình thang cân ABCD có AB // CD, AD = BC và AC = BD → ABCD là hình chữ nhật.

Cách chứng minh hình chữ nhật trong bài toán hình học

Khi làm bài tập hình học, học sinh thường gặp yêu cầu “chứng minh tứ giác là hình chữ nhật”. Để giải, ta cần lựa chọn dấu hiệu phù hợp dựa trên dữ kiện của đề bài.

Trường hợp 1: Dựa vào hình bình hành

Đây là cách thường gặp nhất trong các bài toán lớp 8–9.

Đầu tiên, ta cần chứng minh tứ giác là hình bình hành – tức là có hai cặp cạnh đối song song. Sau đó, chỉ cần chứng minh thêm một trong hai điều kiện sau:

• Hình bình hành đó có một góc vuông
• Hình bình hành đó có hai đường chéo bằng nhau.

Khi một trong hai điều kiện trên được thỏa mãn, tứ giác đó chắc chắn là hình chữ nhật.

Trường hợp 2: Dựa vào tính chất góc

Một tứ giác được xem là hình chữ nhật nếu có ba góc vuông.

Điều này xuất phát từ tính chất tổng bốn góc trong tứ giác luôn bằng 360°. Khi ba góc đã bằng 90°, thì góc còn lại buộc phải là 90° và tứ giác trở thành hình chữ nhật.

Cách chứng minh này thường được dùng khi đề bài cho sẵn các quan hệ vuông góc, giúp học sinh suy luận nhanh mà không cần đến nhiều phép tính phức tạp.

Trường hợp 3: Dựa vào đường chéo

Một dấu hiệu rất quan trọng khác là: Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường thì đó là hình chữ nhật.

Lý do là vì hai đường chéo bằng nhau chứng tỏ hình có tính đối xứng cao, và khi chúng cắt nhau tại trung điểm, bốn góc của tứ giác sẽ tạo thành các góc vuông.

Dấu hiệu này thường dùng trong các bài toán hình tọa độ hoặc bài yêu cầu chứng minh qua quan hệ đường chéo.

Trường hợp 4: Dựa vào hình thang cân

Ngoài ba trường hợp trên, đôi khi ta cũng có thể chứng minh tứ giác là hình chữ nhật dựa trên hình thang cân.

Cụ thể nếu một hình thang cân có hai đường chéo bằng nhau, thì hình đó chính là hình chữ nhật.

Vì trong hình thang cân, hai cạnh bên đã bằng nhau, khi hai đường chéo cũng bằng nhau thì toàn bộ hình trở nên đối xứng và có bốn góc vuông.

Tạm kết

Hiểu đúng dấu hiệu nhận biết hình chữ nhật là nền tảng quan trọng giúp học sinh nắm vững kiến thức hình học phẳng. Việc ghi nhớ và vận dụng linh hoạt các dấu hiệu không chỉ giúp giải bài tập nhanh, chính xác hơn mà còn rèn luyện tư duy logic và khả năng quan sát trong đời sống.

Giáo viên có thể khiến những tiết học toán hình học trở nên sinh động và dễ hiểu hơn khi sử dụng máy chiếu chính hãng tại FPT Shop. Hình ảnh sắc nét, màu sắc chân thực giúp minh họa trực quan từng góc, cạnh và hình khối. Hãy chọn máy chiếu chất lượng cao để nâng cao hiệu quả giảng dạy và khơi gợi hứng thú học tập cho học sinh.

Xem thêm:

Hình chiếu là gì? Cách tìm hình chiếu nhanh, chính xác nhất

Công thức tính diện tích hình chữ nhật chính xác và có ví dụ minh họa

Cách tính diện tích xung quanh hình hộp chữ nhật - Tổng hợp lý thuyết và ví dụ cực dễ hiểu