Công thức nội suy là gì? Đặc điểm, ứng dụng và những lưu ý khi sử dụng công thức

Nội suy tuyến tính, Spline, Lagrange,... là những phương pháp nền tảng trong xử lý dữ liệu. Các phương pháp nội suy này được ứng dụng rộng rãi trong nhiều lĩnh vực như khoa học, kỹ thuật, tài chính và hơn thế nữa. Trong bài viết này, FPT Shop sẽ cùng bạn khám phá nội dung chi tiết về các phương pháp nội suy cũng như cách áp dụng một cách hiệu quả nhất. Cùng tìm hiểu ngay nhé!

Công thức nội suy là gì? Đặc điểm và ứng dụng

Trong quá trình làm việc, bạn sẽ không ít lần gặp những bài toán yêu cầu sử dụng phương pháp nội suy – một công cụ quan trọng giúp tính toán, phân tích và xử lý dữ liệu hiệu quả. Hãy cùng FPT Shop khám phá khái niệm, đặc điểm và ứng dụng thực tế của phương pháp này ngay sau đây!

Khái niệm nội suy

Nội suy là kỹ thuật dùng để ước lượng giá trị của một hàm số dựa trên tập dữ liệu đã biết. Thay vì phải đo đạc hoặc thực nghiệm trực tiếp, chúng ta có thể sử dụng các công thức nội suy để tính toán nhanh chóng và chính xác. Chính nhờ khả năng này, nội suy trở thành một công cụ đắc lực trong việc phân tích dữ liệu rời rạc và tối ưu hóa các quy trình tính toán trong nhiều lĩnh vực khác nhau.

Tính chất và ứng dụng thực tế

Công thức nội suy cho phép chúng ta ước lượng giá trị tại những điểm chưa biết dựa trên tập dữ liệu đã có, đặc biệt hữu ích khi xử lý các dữ liệu rời rạc. Tuy nhiên, độ chính xác của nội suy còn phụ thuộc vào nhiều yếu tố như phương pháp áp dụng, sự phân bố và khoảng cách giữa các điểm dữ liệu. Mỗi phương pháp nội suy sẽ có nguyên lý tính toán riêng, nhưng tất cả đều hướng đến mục tiêu chung: hoàn thiện và bổ sung những thông tin còn thiếu trong dữ liệu.

Công thức nội suy được áp dụng rộng rãi trong nhiều lĩnh vực khoa học và công nghiệp, đặc biệt trong các hoạt động liên quan đến thực nghiệm và xử lý dữ liệu, cụ thể như:

• Trắc địa: Sử dụng ảnh vệ tinh để lập bản đồ bề mặt Trái Đất, từ việc xác định dòng hải lưu cho đến địa hình đồi núi.
• Kỹ thuật: Dự đoán khả năng hoạt động của vật liệu trong những điều kiện khắc nghiệt như nhiệt độ cao hoặc áp suất lớn.
• Phân tích và thống kê: Hỗ trợ ước lượng giá trị của các biến số, xử lý dữ liệu bị thiếu hụt và xây dựng các mô hình dự đoán chính xác.
• Tài chính và kinh tế: Nội suy được sử dụng để dự đoán giá cổ phiếu, phân tích xu hướng thị trường và hỗ trợ ra quyết định đầu tư.

Các công thức nội suy phổ biến

Trong quá trình xử lý dữ liệu và tính toán, có nhiều phương pháp nội suy khác nhau, mỗi phương pháp có cách tiếp cận riêng phù hợp với đặc điểm của dữ liệu. Hãy cùng khám phá các công thức quan trọng dưới đây!

Công thức nội suy tuyến tính

Nội suy tuyến tính là một trong những phương pháp phổ biến nhất, được sử dụng để ước lượng giá trị của hàm số. Phương pháp này dựa trên giả định rằng sự thay đổi giữa hai điểm là tuyến tính.

Sau đây là công thức nội suy tuyến tính giữa (x₀, y₀), (x₁, y₁):

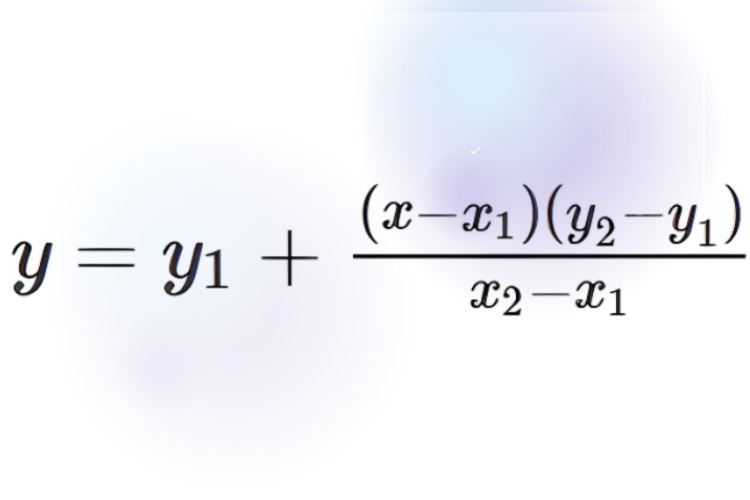
Trong đó:

• y: Giá trị nội suy.
• x: Điểm thực hiện nội suy.
• x₀, y₀: Tọa độ thứ nhất.
• x₁, y₁: Tọa độ thứ hai.

Công thức nội suy đa cấp

Nội suy đa cấp, hay còn gọi là nội suy đa thức, là phương pháp dùng các đa thức đi qua những điểm dữ liệu đã biết để ước lượng giá trị hàm số tại một điểm bất kỳ. Phương pháp này cho độ chính xác cao hơn so với nội suy tuyến tính nhờ sử dụng các đa thức nổi tiếng như đa thức Lagrange hoặc Newton trong quá trình tính toán.

Phương pháp Lagrange: Giả sử chúng ta có n+1 điểm dữ liệu (x₀, y₀), (x₁, y₁), ..., (xₙ, yₙ), thì công thức Lagrange sẽ xây dựng một đa thức nội suy bậc n đi qua tất cả các điểm này như sau:

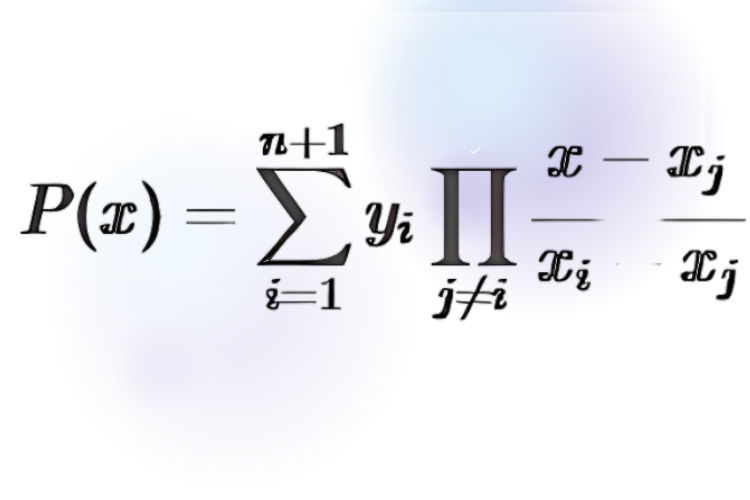
Trong đó:

• P(x): Đa thức nội suy.
• yᵢ: Giá trị của hàm số tại xᵢ.

Phương pháp Newton: Công thức nội suy Newton được xây dựng dựa trên nguyên lý sai phân và được trình bày dưới dạng sau:

Trong đó:

• f[x₀] là giá trị của hàm số tại điểm x₀.
• f[x₀, x₁] là sai phân thứ nhất.

Công thức nội suy Spline

Nội suy Spline là phương pháp sử dụng một chuỗi các đường thẳng hoặc đường cong liên kết liên tục để nối các điểm dữ liệu với nhau. Thay vì dùng một đa thức lớn cho toàn bộ tập dữ liệu, phương pháp này chia nhỏ thành nhiều đoạn, giúp đường nội suy trở nên mượt mà và tự nhiên hơn. Với khả năng giảm nhiễu và xử lý tốt các sai số đo lường, nội suy Spline được ứng dụng rộng rãi trong đồ họa máy tính và nhiều lĩnh vực kỹ thuật.

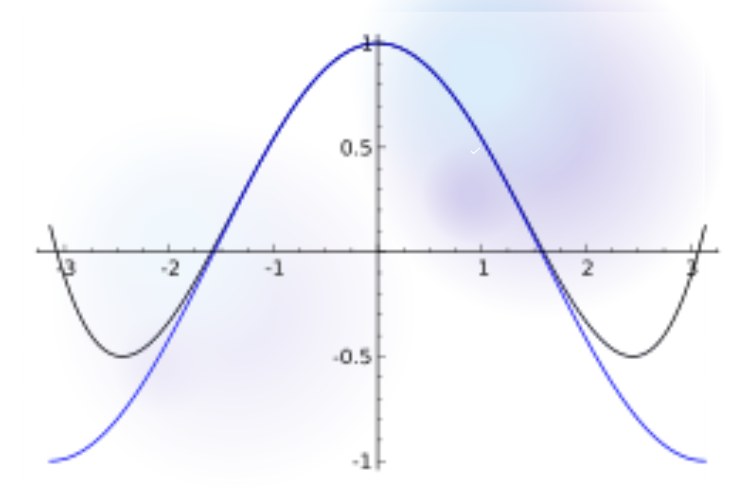
Công thức nội suy bậc thấp

Nội suy bậc thấp là phương pháp sử dụng một số ít điểm dữ liệu để đơn giản hóa quá trình tính toán, phù hợp với những trường hợp cần xử lý nhanh và khi lượng thông tin còn hạn chế. Phương pháp này đặc biệt hữu ích trong các tình huống không yêu cầu độ chính xác quá cao hoặc cần dự đoán giá trị một cách nhanh chóng. Mặc dù không phản ánh đầy đủ xu hướng tổng thể của dữ liệu, các công thức nội suy bậc thấp vẫn mang lại hiệu quả đáng kể trong những bài toán đơn giản.

Ứng dụng phương pháp nội suy trong lĩnh vực xây dựng

Trong ngành xây dựng, độ chính xác là yếu tố quan trọng để đảm bảo chất lượng công trình. Do đó, các kỹ sư thường sử dụng các phương pháp nội suy để hỗ trợ trong việc phân tích, tính toán và tối ưu hóa các vấn đề liên quan đến vật liệu và thiết kế.

Vai trò của công thức nội suy trong xây dựng

Công thức nội suy giúp ước lượng các giá trị còn thiếu. Nhờ đó, kỹ sư có thể tính toán chính xác các thông số như độ lún, độ bền của vật liệu và tải trọng của công trình. Nhờ vào đó, việc lập kế hoạch và quản lý chi phí trở nên hiệu quả hơn, đặc biệt trong trường hợp dữ liệu bị thiếu hoặc gián đoạn.

Công thức nội suy trong lĩnh vực xây dựng

Trong ngành xây dựng, việc xử lý dữ liệu không liên tục là điều phổ biến, chẳng hạn như số liệu đo đạc địa hình, kết quả thí nghiệm vật liệu hoặc thống kê kỹ thuật. Khi không thể thu thập đầy đủ dữ liệu do hạn chế về thời gian hoặc chi phí, bạn có thể sử dụng công thức nội suy sau đây:

• y = y₁ + (x - x₁) * [(y₂ - y₁) / (x₂ - x₁)]

Để áp dụng nội suy một cách chính xác trong xây dựng, bạn cần tuân thủ một quy trình nhất định nhằm đảm bảo độ chính xác và hiệu quả cao nhất. Dưới đây là hướng dẫn chi tiết từ FPT Shop, mời bạn tham khảo.

Bước 1: Chọn điểm dữ liệu

• Chọn các điểm dữ liệu (x, y) từ các thông tin có sẵn để làm cơ sở cho quá trình nội suy.

Bước 2: Lập bảng dữ liệu

• Tạo bảng và sắp xếp các giá trị theo thứ tự tăng dần để thuận tiện cho việc tính toán.

Bước 3: Tính độ chênh lệch

• Tính độ chênh lệch giữa các điểm liên tiếp để xác định khoảng nội suy.

Bước 4: Sử dụng công thức nội suy

• Áp dụng công thức nội suy tuyến tính hoặc công thức phù hợp với nhu cầu của bạn để tìm giá trị cần tính.

Bước 5: Kiểm tra và điều chỉnh

• Kiểm tra kết quả với dữ liệu thực tế và điều chỉnh nếu cần thiết.

Ví dụ về việc tính độ dày vữa tường bằng phương pháp nội suy. Giả sử bạn biết rằng độ dày vữa ở vị trí 4m là 2mm và ở vị trí 10m là 8mm. Bạn muốn tính độ dày vữa tại vị trí 6m.

Áp dụng công thức nội suy tuyến tính:

y = y₁ + [(y₂ - y₁)/(x₂ - x₁)] * (x - x₁).

Ở đây, ta có:

• y₁ = 2 (độ dày tại 4m)
• y₂ = 8 (độ dày tại 10m)
• x₁ = 4
• x₂ = 10
• x = 6.

Thay các giá trị vào công thức: y = 2 + [(8 - 2)/(10 - 4)] * (6 - 4).

Theo đó: y = 2 + [6/6] * 2 = 2 + 2 = 4mm. Vậy, độ dày vữa tường ở vị trí 6m là 4mm.

Tổng hợp các phần mềm hỗ trợ tính toán nội suy

Để hỗ trợ trong việc tính toán các công thức nội suy, bạn có thể tham khảo các phần mềm dưới đây:

1. Microsoft Excel

Excel cung cấp các hàm như LINEST, TREND và FORECAST, giúp bạn thực hiện nội suy một cách nhanh chóng và dễ dàng.

2. MATLAB

MATLAB có các hàm interp1 và interp2, rất phù hợp cho các tính toán khoa học và kỹ thuật liên quan đến nội suy.

3. Python

Sử dụng thư viện NumPy và SciPy, bạn có thể áp dụng các hàm như numpy.interp và scipy.interpolate.griddata để xử lý nội suy phức tạp.

4. Wolfram Alpha

Đây là một công cụ trực tuyến cho phép bạn nhập công thức và tự động nhận kết quả, rất tiện lợi cho việc tính toán nội suy.

Những lưu ý khi sử dụng công thức nội suy chính xác

Nội suy là một công cụ toán học quan trọng, nhưng để đạt được độ chính xác cao, bạn cần lưu ý một số điểm sau:

• Kiểm tra tính đồng nhất của dữ liệu: Trước khi áp dụng công thức nội suy, hãy đảm bảo rằng dữ liệu của bạn nhất quán. Điều này giúp tránh các giá trị ngoại lai có thể làm sai lệch kết quả.
• Chọn phương pháp nội suy phù hợp: Lựa chọn phương pháp nội suy dựa trên tính chất của dữ liệu. Sử dụng nội suy tuyến tính cho dữ liệu đơn giản, trong khi Spline hoặc đa thức là lựa chọn tốt cho các trường hợp phức tạp hơn.
• Hạn chế nội suy ngoài phạm vi dữ liệu: Tránh nội suy ở ngoài phạm vi dữ liệu có sẵn, vì điều này có thể dẫn đến sai số lớn.
• Đảm bảo lượng dữ liệu đủ lớn: Có một lượng dữ liệu đủ lớn là rất quan trọng. Nếu dữ liệu quá ít, độ chính xác của kết quả sẽ bị giảm.

Lời kết

Trên đây là thông tin tổng hợp về các công thức nội suy tuyến tính, Spline và nhiều phương pháp khác. Nhờ khả năng xử lý dữ liệu hiệu quả, nội suy được ứng dụng rộng rãi trong các lĩnh vực khoa học, kỹ thuật và nhiều lĩnh vực khác. Hy vọng rằng qua bài viết này, bạn đã nắm rõ hơn về các phương pháp nội suy và có thể áp dụng chúng một cách hiệu quả trong thực tế!

Nếu bạn đang tìm kiếm chiếc smartphone có thể tìm kiếm thông tin nhanh chóng mọi lúc, mọi nơi có thể đến ngay FPT Shop để được tư vấn chi tiết. Tại FPT Shop đang kinh doanh nhiều mẫu smartphone chất lượng từ những thương hiệu hàng đầu, giúp bạn yên tâm chọn được sản phẩm phù hợp, sử dụng dài lâu.

Tham khảo điện thoại Xiaomi ngay tại đây: 

• Xiaomi

Xem thêm

• Công thức biến cố độc lập là gì? Ví dụ minh họa và các dạng bài tập thường gặp
• Tổng hợp các phương pháp chứng minh tứ giác nội tiếp và một số bài tập vận dụng
• Tuyến tính là gì? Ý nghĩa, ứng dụng và phân tích khái niệm trong nhiều lĩnh vực