Công thức biến cố độc lập là gì? Ví dụ minh họa và các dạng bài tập thường gặp

Khi nói đến biến cố độc lập, ta đang nhắc tới những sự kiện xảy ra mà không hề ảnh hưởng đến xác suất của nhau. Hiểu đơn giản, việc một sự kiện diễn ra hay không cũng chẳng làm thay đổi khả năng xảy ra của sự kiện kia. Trong lĩnh vực xác suất, nắm vững khái niệm này sẽ giúp bạn phân tích các tình huống chuẩn xác và khoa học hơn.

Hãy cùng FPT Shop khám phá chi tiết về định nghĩa biến cố độc lập là gì, công thức liên quan đến biến cố độc lập, đồng thời xem qua các ví dụ thực tế có lời giải, để bạn dễ dàng vận dụng trong học tập và đời sống nhé!

Biến cố độc lập là gì?

Trong lý thuyết xác suất, hai biến cố A và B được xem là độc lập nếu việc A xảy ra hay không xảy ra hoàn toàn không ảnh hưởng đến xác suất xảy ra của B. Hiểu một cách đơn giản, dù A có diễn ra hay không thì khả năng B xảy ra vẫn không thay đổi.

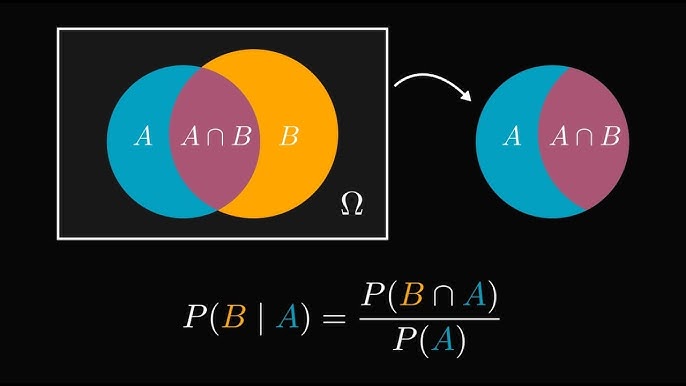
Quy tắc nhân xác suất

Khi hai biến cố A và B độc lập với nhau, xác suất để cả A và B cùng xảy ra được tính bằng cách nhân xác suất của từng biến cố lại với nhau:

• P(AB) = P(A) × P(B)

Quy tắc này cũng áp dụng tương tự cho nhiều biến cố hơn. Nếu có k biến cố A1, A2, ..., Ak và tất cả đều độc lập, thì xác suất để cả k biến cố đó xảy ra cùng lúc sẽ bằng tích xác suất của từng biến cố:

• P(A1A2...Ak) = P(A1) × P(A2) × ... × P(Ak)

Ví dụ minh họa về biến cố độc lập

Sau khi đã nắm rõ biến cố độc lập là gì, hãy cùng đi đến ví dụ minh họa. Giả sử một chiếc máy bay có hai động cơ, gọi là động cơ I và động cơ II. Hai động cơ này làm việc độc lập với nhau, nghĩa là hiệu suất của động cơ này không hề tác động đến động cơ kia. Biết rằng xác suất để động cơ I hoạt động bình thường là 0,6, còn động cơ II có xác suất hoạt động tốt là 0,8. Hãy cùng tính:

a) Xác suất để cả hai động cơ cùng hoạt động tốt.

b) Xác suất để cả hai động cơ đều gặp trục trặc, không hoạt động.

Cách giải chi tiết:

a) Tính xác suất cả hai động cơ đều vận hành tốt

Vì động cơ I và động cơ II hoạt động độc lập với nhau, nên xác suất để cả hai cùng chạy tốt sẽ bằng tích xác suất từng động cơ hoạt động ổn định:

P(A) = P(động cơ I tốt) × P(động cơ II tốt) = 0,6 × 0,8 = 0,48

b) Tính xác suất cả hai động cơ đều bị hỏng

Đầu tiên, ta xác định xác suất mỗi động cơ bị hỏng:

• Xác suất động cơ I hỏng: P(I hỏng) = 1 - 0,6 = 0,4
• Xác suất động cơ II hỏng: P(II hỏng) = 1 - 0,8 = 0,2

Vì hai động cơ hỏng độc lập, xác suất để cả hai cùng hỏng là:

• P(B) = P(I hỏng) × P(II hỏng) = 0,4 × 0,2 = 0,08

Như vậy, xác suất để cả hai động cơ cùng hoạt động tốt là 48%, trong khi xác suất cả hai đều hỏng chỉ chiếm 8%. Đây là một ví dụ sinh động cho thấy cách vận dụng quy tắc nhân xác suất đối với các biến cố độc lập, đồng thời giúp chúng ta hiểu rõ hơn về mức độ an toàn khi vận hành các thiết bị kỹ thuật.

Bài tập tự luyện về biến cố độc lập

Để giúp bạn rèn luyện thêm kỹ năng nhận biết và tính xác suất của các biến cố độc lập là gì, hãy cùng thử sức với bài tập sau:

Bài 1: Một chiếc máy bay sử dụng hai động cơ A và B. Hai động cơ này làm việc hoàn toàn độc lập, tức là hiệu suất của động cơ này không ảnh hưởng gì đến động cơ kia. Theo số liệu kỹ thuật, xác suất để động cơ A vận hành bình thường là 0,5, còn xác suất để động cơ B hoạt động ổn định là 0,9.

Dựa trên thông tin đó, hãy tính:

a) Xác suất để cả hai động cơ đều hoạt động tốt.

b) Xác suất để cả hai động cơ đều bị hỏng.

Một số bài tập luyện tập về biến cố độc lập

Bài 2: Trong một trò chơi may rủi, ta tiến hành gieo một con xúc xắc đều hai lần liên tiếp. Xét hai biến cố:

A: "Lần gieo thứ nhất ra mặt 4 chấm"

B: "Lần gieo thứ hai ra mặt 4 chấm"

Bạn hãy cho biết: hai biến cố A và B có phải là biến cố độc lập hay không? Hãy trình bày rõ lý do.

Bài 3: Giả sử A và B là hai biến cố xung khắc, nghĩa là chúng không thể xảy ra cùng lúc, đồng thời biết rằng P(A) > 0 và P(B) > 0. Hãy chứng minh rằng trong trường hợp này, A và B không thể là hai biến cố độc lập.

Lời kết

Qua bài viết trên, FPT Shop đã giúp bạn giải thích: ”Biến cố độc lập là gì?”. Việc hiểu đúng về biến cố độc lập sẽ giúp chúng ta vận dụng các quy tắc xác suất một cách chính xác trong nhiều tình huống thực tế. Thông qua những ví dụ minh họa và bài tập ở trên, bạn đã có thể hình dung rõ hơn cách nhận diện cũng như tính toán xác suất liên quan đến các biến cố này.

Nếu bạn là học sinh và đang tìm kiếm một chiếc laptop phục vụ cho việc học tập hiệu quả, hãy ghé ngay FPT Shop để khám phá các mẫu laptop học sinh phù hợp với nhu cầu học online, nghiên cứu, làm bài tập và giải trí. 

Mời bạn tham khảo dòng laptop Lenovo chất lượng với nhiều ưu đãi hấp dẫn tại đây:

• Laptop Lenovo

Xem thêm

• Biến cố xung khắc là gì? Có điểm gì khác với biến cố độc lập?
• Cách sử dụng công thức tính phần trăm khối lượng chính xác và hiệu quả nhất
• Bảng tính tan trong hóa học: Ý nghĩa, cách đọc, ứng dụng và các quy tắc ghi nhớ quan trọng