Biến cố xung khắc là gì? Phân biệt giữa biến cố độc lập và biến cố xung khắc

Trong xác suất thống kê, việc nhận diện và phân loại các loại biến cố là bước quan trọng để giải quyết bài toán chính xác. Trong đó, khái niệm biến cố xung khắc thường gây nhầm lẫn với biến cố độc lập bởi chúng đều liên quan đến mối quan hệ giữa các sự kiện. Hiểu rõ sự khác biệt sẽ giúp bạn nắm chắc bản chất của từng loại biến cố và áp dụng đúng trong từng tình huống. Hãy cùng FPT Shop đi sâu tìm hiểu định nghĩa, đặc điểm và cách phân biệt giữa biến cố độc lập và biến cố xung khắc.

Khái quát về biến cố trong xác suất

Trong xác suất thống kê, mối quan hệ giữa các biến cố giữ vai trò quan trọng khi phân tích một phép thử hay nhiều lần quan sát. Hai khái niệm thường được nhắc đến là biến cố xung khắc và biến cố độc lập, mỗi loại phản ánh mối quan hệ khác nhau giữa các sự kiện.

Biến cố xung khắc

Biến cố xung khắc là khi hai sự kiện không thể cùng xảy ra trong cùng một phép thử. Nói cách khác, nếu biến cố A diễn ra thì biến cố B chắc chắn không xảy ra, và ngược lại. Về mặt toán học, giao của A và B là tập rỗng, đồng nghĩa với việc xác suất để cả hai xảy ra đồng thời bằng 0. Trong trường hợp này, quy tắc cộng xác suất được sử dụng, theo đó: Xác suất để A hoặc B xảy ra bằng tổng xác suất của từng biến cố.

Biến cố độc lập

Biến cố độc lập phản ánh mối quan hệ khi sự xuất hiện hay không xuất hiện của một sự kiện không ảnh hưởng đến xác suất xảy ra của sự kiện khác. Nếu A và B là hai biến cố độc lập, thì xác suất để chúng đồng thời xảy ra chính là tích của xác suất từng biến cố riêng lẻ. Điều này cho thấy hai sự kiện có thể cùng diễn ra nhưng hoàn toàn không tác động đến khả năng xuất hiện của nhau.

So sánh biến cố độc lập và biến cố xung khắc

Nguyên tắc xác suất đối với biến cố độc lập và biến cố xung khắc

Đối với biến cố độc lập

Trong lý thuyết xác suất, biến cố độc lập là các sự kiện mà việc xảy ra hay không xảy ra của một sự kiện không ảnh hưởng đến xác suất của sự kiện khác. Khi đó, ta áp dụng công thức:

Với hai biến cố độc lập A và B, xác suất đồng thời xảy ra của chúng được tính như sau:

Đối với biến cố xung khắc

Biến cố xung khắc là những sự kiện loại trừ nhau, nghĩa là khi một sự kiện xảy ra thì sự kiện kia không thể xảy ra đồng thời. Trong trường hợp này, ta dùng quy tắc cộng xác suất:

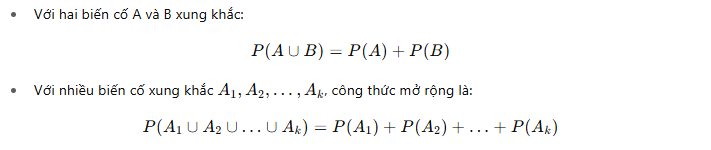
Ứng dụng thực tế của biến cố độc lập và biến cố xung khắc

Trong cuộc sống và nghiên cứu khoa học, ta dễ dàng bắt gặp những tình huống phản ánh mối quan hệ giữa các biến cố độc lập và biến cố xung khắc. Một vài ví dụ điển hình dưới đây sẽ giúp hình dung rõ ràng hơn:

• Ví dụ về biến cố độc lập: Khi tung một đồng xu và một con xúc xắc, kết quả của đồng xu (ngửa hoặc sấp) hoàn toàn không tác động đến kết quả của xúc xắc (1 đến 6). Đây là hai biến cố độc lập.
• Ví dụ về biến cố xung khắc: Trong một bộ bài tây, nếu rút một lá, biến cố “rút được Át cơ” và “rút được Át rô” không thể xảy ra đồng thời, vì bạn chỉ chọn được một lá duy nhất tại mỗi lần rút.
• Ví dụ từ lĩnh vực xác suất: Khi gieo xúc xắc, giả sử A là biến cố “xuất hiện số từ 4 trở lên” và B là biến cố “xuất hiện số từ 2 trở xuống”. Hai biến cố này loại trừ nhau, nghĩa là xung khắc.
• Ví dụ trong thương mại: Một cửa hàng đưa ra hai chương trình giảm giá, một dành cho sản phẩm điện tử và một cho sản phẩm gia dụng. Khách hàng chỉ được áp dụng một trong hai, vì thế hai sự kiện này cũng xung khắc.

Những ví dụ trên cho thấy sự khác biệt giữa biến cố độc lập và biến cố xung khắc trong đời sống thường ngày, đồng thời nhấn mạnh tầm quan trọng của việc áp dụng đúng quy tắc xác suất để phân tích và dự đoán.

Bài tập minh họa về biến cố độc lập và biến cố xung khắc

Để hiểu sâu hơn các khái niệm trong xác suất, việc thực hành thông qua những bài tập cụ thể là rất cần thiết. Dưới đây là một số ví dụ giúp củng cố kiến thức và rèn luyện kỹ năng áp dụng quy tắc tính toán cho từng loại biến cố:

• Bài tập 1: Tung một đồng xu hai lần. Gọi A là biến cố “xuất hiện mặt sấp ở lần đầu”, B là biến cố “xuất hiện mặt sấp ở lần thứ hai”. Hãy chứng minh A và B là các biến cố độc lập, đồng thời tính xác suất của chúng.
• Bài tập 2: Trong một túi có 5 viên bi xanh và 3 viên bi đỏ. Rút ngẫu nhiên hai viên liên tiếp, tính xác suất để lần đầu rút được bi xanh và lần hai rút được bi đỏ. Chứng minh rằng hai biến cố này thuộc loại xung khắc.
• Bài tập 3: Có ba người cùng bắn vào bia. Xác suất bắn trúng lần lượt là 0.7, 0.8 và 0.6. Hãy tính xác suất để có ít nhất một người bắn trúng, đồng thời xác định mối quan hệ giữa các biến cố này có phải là độc lập hay không.

Thông qua các dạng bài tập trên, người học sẽ nắm vững định nghĩa, cách phân biệt và phương pháp tính toán xác suất đối với biến cố độc lập và biến cố xung khắc, từ đó áp dụng hiệu quả trong cả lý thuyết và thực tiễn.

Tạm kết

Qua những thông tin trên, có thể thấy rằng việc nắm vững khái niệm biến cố xung khắc và phân biệt rõ với biến cố độc lập không chỉ giúp làm sáng tỏ lý thuyết xác suất, mà còn tạo nền tảng để vận dụng vào nhiều tình huống thực tế. Sự hiểu biết này sẽ hỗ trợ người học đưa ra những đánh giá chính xác hơn khi phân tích dữ liệu, dự đoán sự kiện và giải quyết các bài toán xác suất một cách hiệu quả.

Bạn muốn học xác suất một cách hiệu quả và thuận tiện hơn? Laptop với hiệu năng ổn định và màn hình rộng sẽ giúp bạn dễ dàng chạy phần mềm, làm bài tập và trực quan hóa dữ liệu. Hãy chọn ngay một chiếc laptop HP phù hợp để nâng tầm trải nghiệm học tập của bạn!

• Laptop HP

Xem thêm:

• Hướng dẫn chi tiết cách tính xác suất nhanh chóng, hiệu quả và các bài toán minh hoạ cụ thể
• Hợp số là gì? Giải mã bản chất của hợp số và các ứng dụng cụ thể trong Toán học