Hướng dẫn chi tiết cách tính xác suất nhanh chóng, hiệu quả và các bài toán minh hoạ cụ thể

Trong toán học cũng như đời sống, xác suất đóng vai trò quan trọng trong việc dự đoán các kết quả có thể xảy ra của một biến cố. Để có thể tính toán chính xác thì việc hiểu rõ các công thức là điều cần thiết. Bài viết này sẽ hướng dẫn cách tính xác suất giúp bạn tự tin trong mọi tình huống.

Các công thức tính tổ hợp

Tổ hợp là một khái niệm cơ bản trong xác suất, đặc biệt khi ta cần xác định số lượng các cách sắp xếp hay chọn lựa từ một tập hợp nhất định. Có hai loại tổ hợp chính là tổ hợp lặp và tổ hợp không lặp.

Tổ hợp lặp

Trong quá trình giải các bài toán tính xác suất, việc tính toán tổ hợp lặp là chìa khóa quan trọng để giải quyết những vấn đề phức tạp. Tổ hợp lặp là trường hợp khi mỗi phần tử trong tập hợp có thể được chọn nhiều lần.

Giả sử, chúng ta làm việc với một tập hợp A gồm n phần tử, cần chọn ra k phần tử từ tập A. Mỗi phần tử trong số k có thể được chọn lặp lại nhiều lần. Tổ hợp lặp chập k của tập A có n phần tử được hiểu là một tập con gồm k phần tử, trong đó mỗi phần tử trong tập A có thể xuất hiện nhiều lần. Công thức tính tổ hợp lặp được xác định như sau:

Cnk = Cn+k−1k + Cn+k−1m−1

Tổ hợp không lặp

Trong tính xác suất, tổ hợp không lặp cũng là khái niệm quan trọng. Tổ hợp không lặp là trường hợp khi mỗi phần tử trong tập hợp chỉ có thể được chọn một lần. 

Cụ thể với tập hợp A gồm n phần tử, tổ hợp không lặp chập k của n là một tập con gồm k phần tử từ A. Trong đó, mỗi phần tử chỉ được chọn một lần (với 1  k   n). Công thức tính tổ hợp không lặp như sau:

Cnk  = Ank / k! = n!/ k! (n − k)!

Cách tính xác suất của biến cố

Xác suất của một biến cố là khả năng xảy ra của biến cố đó. Việc tính xác suất của một biến cố giúp bạn định hướng và đưa ra những dự đoán chính xác nhất. Giá trị của nó luôn nằm trong khoảng từ 0 đến 1. Trong đó 0 biểu thị biến cố không thể xảy ra, còn 1 cho biết chắc chắn sẽ xảy ra.

Để tính xác suất của một biến cố, bước đầu tiên là xác định rõ hai yếu tố quan trọng: không gian mẫu, bao gồm tất cả các kết quả có thể xảy ra trong phép thử và biến cố cần xét thức tập hợp các kết quả cụ thể mà ta quan tâm. Sau khi xác định, bạn có thể áp dụng công thức tính xác suất như sau:

P(A) = n(A) / n(Ω)

Trong đó:

• P(A) là xác suất của biến cố A.
• n(A) là số trường hợp thuận lợi cho A.
• n(Ω) là tổng số trường hợp có thể xảy ra.

Việc nắm vững cách định nghĩa và công thức tính xác suất sẽ giúp bạn đưa ra những dự đoán chính xác hơn trong những tình huống bí ẩn nhất. Từ việc dự báo thời tiết đến phân tích các trò chơi may rủi.

Ví dụ: Nếu bạn tung một đồng xu, xác suất để đồng xu rơi vào mặt ngửa là P(ngửa)=½. Vì n(A) khả năng xuất hiện mặt ngừa là 1, n() các trường hợp có thể xảy ra là 2 ngửa và sấp.

Tổng hợp các công thức tính xác suất thống kê

Xác suất thống kê là một công cụ mạnh mẽ để phân tích và dự đoán trong nhiều lĩnh vực khác nhau. Dưới đây là các công thức xác suất quan trọng:

Công thức cộng xác suất

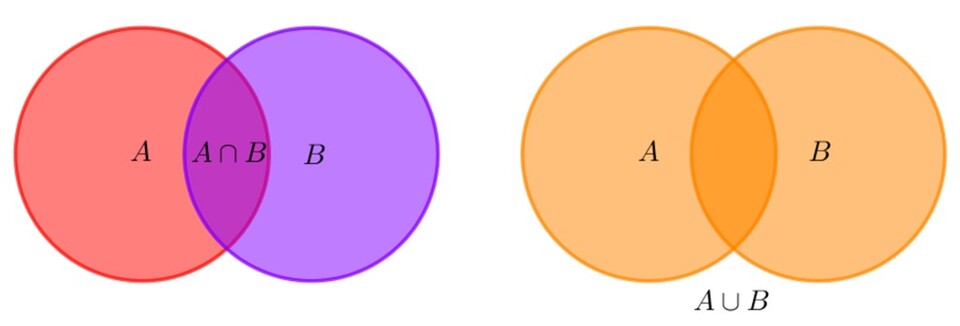
Công thức cộng xác suất được áp dụng khi bạn muốn tính xác suất của ít nhất một trong hai biến cố xảy ra. Cụ thể với hai biến cố A và B, xác suất để ít nhất một trong hai biến cố xảy ra được tính bằng cách cộng xác suất của từng biến, sau đó trừ đi xác suất mà cả hai biến cố cùng xảy ra. Phương pháp này đảm bảo tính toán chính xác ngay cả các trường hợp phức tạp, giúp đưa ra quyết định dựa trên cơ sở khoa học chặt chẽ.

P(AB) = P(A) + P(B) - P(AB)

Công thức xác suất đồng thời

Công thức xác suất đồng thời được sử dụng để tính xác suất của hai biến cố cùng xảy ra. Công thức xác suất đồng thời cho phép tính toán dựa trên xác suất của từng biến cố và xác suất có điều kiện của biến cố thứ hai khi biết biến cố đầu tiên đã xảy ra.

P(AB) = P(A) x P(BlA)

Công thức xác suất điều kiện

Xác suất điều kiện là xác suất của một biến cố xảy ra dựa trên điều kiện rằng một biến cố khác đã xảy ra. Công thức tính xác suất có điều kiện được sử dụng để đánh giá khả năng xảy ra của một biến cố khi có thông tin về biến cố khác. Bằng cách sử dụng công thức này, chúng ta có thể cập nhật xác suất dựa trên dữ liệu mới, từ đó đưa ra các quyết định chính xác và kịp thời.

P(B∣A)=P(A)P(A∩B)​

Công thức xác suất biên

Xác suất biên là xác suất của một biến cố xảy ra mà không quan tâm đến các biến cố khác. Công thức tính xác suất biên giúp tính toán dễ dàng và chính xác bằng cách loại bỏ ảnh hưởng của những biến cố không liên quan. Điều này cho phép tập trung vào việc phân tích xác suất của biến cố chính.

P(A)=i∑​P(A∩Bi​)

Trong đó:

• P(A∩Bi​) là xác suất chung của $AA$$P(A\cap B_i)P(A\; \backslash cap\; B\_i)$
• ${\sum }_i\backslash sum\_\{i\}$$BB$$BB$

Nếu $BB$B là biến liên tục, thì công thức sẽ là tích phân thay vì tổng:

P(A)=∫P(A∩B)dB

Các bài toán minh họa về tính xác suất

Sau khi nắm được các công thức tính xác suất, để hình dung rõ hơn trong việc áp dụng vào thực tế. Dưới đây là các bài toán minh họa cụ thể.

Bài toán rút bài ngẫu nhiên

Bộ bài tú - lơ khơ có 52 quân bài. Rút ngẫu nhiên ra 4 quân bài. Tìm xác suất của các biến cố A: "Rút ra được tứ quý K ‘’

Lời giải:

• Ta có số cách chọn ngẫu nhiên 4 quân bài là: C524 = 270725.
• Vì bộ bài chỉ có 1 tứ quý K nên ta có n(A)=1.
• Vậy P(A) = 1 /270725.

Bài toán lấy bi ngẫu nhiên

Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tìm xác suất để 3 viên bi lấy ra đều màu đỏ.

Lời giải:

• Gọi biến cố A :" 3 viên bi lấy ra đều màu đỏ".
• Số các lấy 3 viên bi từ 20 viên bi là: C203 nên ta có n() = C203 = 1140.
• Số cách lấy 3 viên bi màu đỏ là: C83  nên ta có n(A) = C83 = 56.
• Vậy  P(A) = n(A) / n() = 56 / 1140 = 14/285.

Lưu ý để tính xác suất hiệu quả

Khi áp dụng cách tính xác suất, có một số lưu ý quan trọng mà bạn nên xem xét để đảm bảo rằng bạn đang làm đúng và đạt được kết quả chính xác. 

• Xác định không gian mẫu: Trước khi tính xác suất, bạn cần xác định không gian mẫu (tập hợp tất cả các kết quả có thể xảy ra trong một thí nghiệm). Việc này giúp bạn có cái nhìn tổng quan về các khả năng có thể xảy ra.
• Phân loại các kiểu xác suất: Có nhiều loại xác suất như xác suất cổ điển, xác suất thống kê và xác suất chủ quan. Tùy thuộc vào ngữ cảnh, bạn sẽ chọn phương pháp tính xác suất phù hợp.
• Xem xét tính độc lập: Nếu các sự kiện là độc lập, xác suất của sự kiện đồng thời xảy ra sẽ là tích của xác suất của mỗi sự kiện. Hãy kiểm tra xem các sự kiện có độc lập hay không.
• Cẩn thận với thông tin thiên lệch: Đôi khi, xác suất có thể bị ảnh hưởng bởi thông tin không đầy đủ hoặc sai lệch. Hãy chắc chắn rằng bạn sử dụng dữ liệu chính xác và quan trọng.
• Kiểm tra kết quả: Sau khi tính toán, bạn nên kiểm tra lại kết quả của mình. Việc lập bảng hoặc vẽ một đồ thị có thể giúp xác định xem các giá trị tính toán có hợp lý hay không.

Tạm kết

Việc nắm vững các công thức tính tổ hợp và các công thức tính xác suất thống kê là vô cùng cần thiết trong nhiều lĩnh vực, từ toán học, kinh tế, cho đến các ngành khoa học xã hội. Hiểu rõ và áp dụng chính xác các công thức này sẽ giúp bạn có được những phân tích và dự đoán chính xác hơn trong công việc và cuộc sống hàng ngày.

Nếu bạn cần tìm kiếm công cụ hỗ trợ nghiên cứu, học tập toán học hàng ngày thì hãy tham khảo các dòng laptop tại FPT Shop. Tại đây không chỉ cung cấp hàng chính hãng mà còn cam kết mang lại sản phẩm giá tốt, mẫu mã đẹp mắt, tư vấn nhiệt tình để bạn yên tâm mua hàng.

Máy tính xách tay

Bạn có thể xem thêm:

• 6 ứng dụng toán học tốt và dễ dùng nhất cho học sinh cấp 1
• Số nguyên là gì? Hiểu rõ bản chất, cách phân loại và ứng dụng của số nguyên trong toán học