Tuyến tính là gì? Ý nghĩa, ứng dụng và phân tích khái niệm trong nhiều lĩnh vực

Nhiều người khi bắt gặp khái niệm “tuyến tính” thường nghĩ ngay đến sự thẳng hàng hoặc mối quan hệ đều đặn giữa các đại lượng. Tuy nhiên, để trả lời chính xác câu hỏi tuyến tính là gì, chúng ta cần đi sâu hơn vào lý thuyết và ứng dụng. Từ toán học đến kinh tế, từ công nghệ đến đời sống, khái niệm này hiện diện ở nhiều lĩnh vực khác nhau và mang những giá trị rất riêng. Bài viết này sẽ giúp bạn hình dung một cách rõ ràng, đầy đủ và có hệ thống về tuyến tính, đồng thời chỉ ra vì sao đây là nền tảng quan trọng trong nghiên cứu cũng như thực tiễn.

Tuyến tính là gì?

Khái niệm tuyến tính xuất phát từ gốc Latinh “linea” có nghĩa là đường thẳng. Ở mức độ phổ quát, tính tuyến tính được hiểu là mối quan hệ thẳng hàng, cân đối hoặc có sự thay đổi đồng đều giữa các yếu tố. Trong nhiều ngành khoa học, tuyến tính thể hiện qua mối quan hệ tỉ lệ thuận giữa các biến, nghĩa là khi một biến tăng lên hoặc giảm xuống, biến còn lại cũng thay đổi theo cùng một quy luật nhất định.

Tuyến tính không chỉ là khái niệm lý thuyết mà còn trở thành công cụ quan trọng để mô hình hóa, dự đoán và phân tích dữ liệu. Từ toán học đại số tuyến tính, vật lý sóng, kỹ thuật mạch điện đến các ngành kinh tế học, sự xuất hiện của khái niệm này đều mang tính nền tảng.

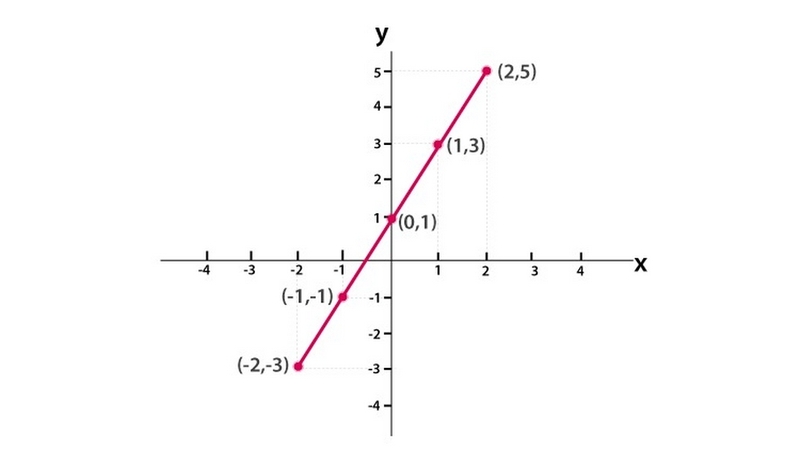
Đặc điểm nổi bật của tính tuyến tính

Để hiểu sâu hơn tuyến tính là gì, cần nắm rõ những đặc điểm cơ bản:

• Quan hệ tỉ lệ thuận: Khi biến đầu vào thay đổi, biến đầu ra biến đổi theo tỷ lệ cố định.
• Tính chất cộng hưởng: Tổng của các đầu vào tuyến tính bằng tổng của các đầu ra tuyến tính.
• Tính đồng nhất: Nếu đầu vào tăng gấp đôi thì kết quả đầu ra cũng tăng gấp đôi, duy trì tỷ lệ không đổi.
• Khả năng mô hình hóa: Tính tuyến tính cho phép mô hình hóa nhiều hiện tượng phức tạp thành dạng đơn giản hơn, giúp việc phân tích dễ dàng.

Tuyến tính trong toán học và khoa học tự nhiên

Đại số tuyến tính

Đại số tuyến tính là lĩnh vực nghiên cứu các không gian vectơ và phép biến đổi tuyến tính. Đây là công cụ nền tảng cho hầu hết các ngành khoa học, đặc biệt trong phân tích dữ liệu, trí tuệ nhân tạo và đồ họa máy tính.

Phương trình tuyến tính

Một phương trình tuyến tính thường có dạng bậc nhất, thể hiện mối quan hệ đơn giản giữa hai hay nhiều biến. Nhờ đặc điểm dễ tính toán và dự đoán, phương trình tuyến tính là điểm khởi đầu cho nhiều bài toán lớn hơn.

Tuyến tính trong vật lý

Trong vật lý, nhiều hiện tượng như dao động điều hòa, sóng cơ học, mạch điện xoay chiều được mô hình hóa bằng phương trình tuyến tính. Nhờ đó, các nhà khoa học dễ dàng dự đoán hành vi của hệ thống và ứng dụng trong kỹ thuật.

Tuyến tính trong kinh tế và xã hội

Mô hình kinh tế tuyến tính

Trong kinh tế, tuyến tính giúp phân tích mối quan hệ giữa cung và cầu, giá cả và sản lượng. Khi giá tăng gấp đôi, lượng cầu có thể giảm theo một tỷ lệ nhất định, phản ánh tính chất tuyến tính trong hành vi thị trường.

Quản lý và dự báo

Khái niệm tuyến tính cũng được dùng trong quản trị để mô phỏng tốc độ tăng trưởng doanh nghiệp, phân tích dữ liệu bán hàng hoặc dự đoán xu hướng tiêu dùng. Dù thực tế thường phức tạp, các mô hình tuyến tính vẫn được áp dụng rộng rãi nhờ tính đơn giản và dễ hiểu.

Ứng dụng thực tiễn của tuyến tính

Trong công nghệ và kỹ thuật

Các hệ thống điện tử, mạch khuếch đại, tín hiệu số đều vận hành dựa trên nguyên lý tuyến tính. Điều này giúp việc xử lý dữ liệu trở nên chính xác và hiệu quả hơn.

Trong trí tuệ nhân tạo

Học máy và trí tuệ nhân tạo ứng dụng mô hình hồi quy tuyến tính để phân tích và dự đoán. Đây là bước nền quan trọng cho các thuật toán phức tạp hơn như mạng nơ-ron nhân tạo.

Trong đời sống hàng ngày

Khái niệm tuyến tính không chỉ xuất hiện trong học thuật mà còn trong đời sống. Ví dụ, khi bạn tăng gấp đôi số giờ học đều đặn, kết quả cải thiện theo hướng tuyến tính. Điều này thể hiện tính đều đặn và dự đoán được.

Lợi ích của việc hiểu tuyến tính là gì?

Hiểu được tuyến tính giúp người học và người làm việc trong nhiều lĩnh vực dễ dàng:

• Xây dựng các mô hình dự đoán có độ chính xác cao.
• Tối ưu hóa quy trình sản xuất và quản lý.
• Dễ dàng phân tích và diễn giải dữ liệu phức tạp.
• Hiểu rõ hơn về bản chất của các hiện tượng tự nhiên và xã hội.

Tuyến tính và phi tuyến tính: So sánh và khác biệt

Khi đặt câu hỏi tuyến tính là gì, ta cũng cần phân biệt nó với phi tuyến tính.

• Tuyến tính: Quan hệ tỉ lệ thuận, thay đổi đều đặn, dễ dự đoán.
• Phi tuyến tính: Quan hệ phức tạp, không theo quy luật cố định, thay đổi bất ngờ và khó dự đoán.

Ví dụ, sự tăng trưởng của dân số trong điều kiện ổn định có thể xem là tuyến tính, nhưng khi có yếu tố dịch bệnh, thiên tai, kết quả trở nên phi tuyến tính.

Ý nghĩa của tuyến tính trong học tập và nghiên cứu

Đối với học sinh, sinh viên, việc hiểu tuyến tính là gì sẽ giúp tiếp cận các môn học như toán, vật lý, kinh tế một cách dễ dàng hơn. Với các nhà nghiên cứu, tuyến tính là nền móng để phát triển các mô hình phức tạp. Còn trong đời sống, nó giúp mỗi người có cách nhìn rõ ràng về mối quan hệ nhân quả, từ đó đưa ra quyết định hợp lý.

Kết luận

Qua bài viết, có thể thấy tuyến tính là khái niệm xuyên suốt trong toán học, khoa học, kinh tế và cả đời sống thường ngày. Việc hiểu rõ tuyến tính là gì không chỉ hỗ trợ học tập, nghiên cứu mà còn giúp chúng ta dễ dàng đưa ra dự đoán, phân tích và giải quyết vấn đề. Nhờ tính đơn giản và khả năng ứng dụng cao, tuyến tính trở thành một công cụ hữu ích cho mọi lĩnh vực.

Nếu bạn quan tâm đến công nghệ, học tập hoặc các lĩnh vực ứng dụng tính toán, đừng quên tham khảo các dòng laptop học tập – làm việc tại FPT Shop. Những sản phẩm này sẽ đồng hành cùng bạn trong việc phân tích dữ liệu, nghiên cứu và phát triển kỹ năng số:

• Laptop sinh viên - văn phòng

Xem thêm: 

• Công thức nội suy là gì? Đặc điểm, ứng dụng và những lưu ý khi sử dụng công thức
• Định tuyến là gì? Những điều cần biết và tác động của định tuyến trong kết nối mạng