Tích vô hướng của hai vectơ: Định nghĩa, công thức tính toán và ứng dụng chi tiết

Trong toán học, đặc biệt là trong đại số tuyến tính và hình học giải tích, tích vô hướng của hai vectơ là một phép toán quan trọng giúp xác định góc giữa hai vectơ, kiểm tra tính vuông góc. Không chỉ trong toán học thuần túy, tích vô hướng của hai vectơ còn có ứng dụng thực tiễn rộng rãi trong kỹ thuật và khoa học máy tính. Bài viết này FPT Shop sẽ giúp bạn hiểu rõ về định nghĩa, công thức tính toán và ứng dụng của tích vô hướng của hai vectơ trong các lĩnh vực khác nhau.

Định nghĩa tích vô hướng của hai vectơ

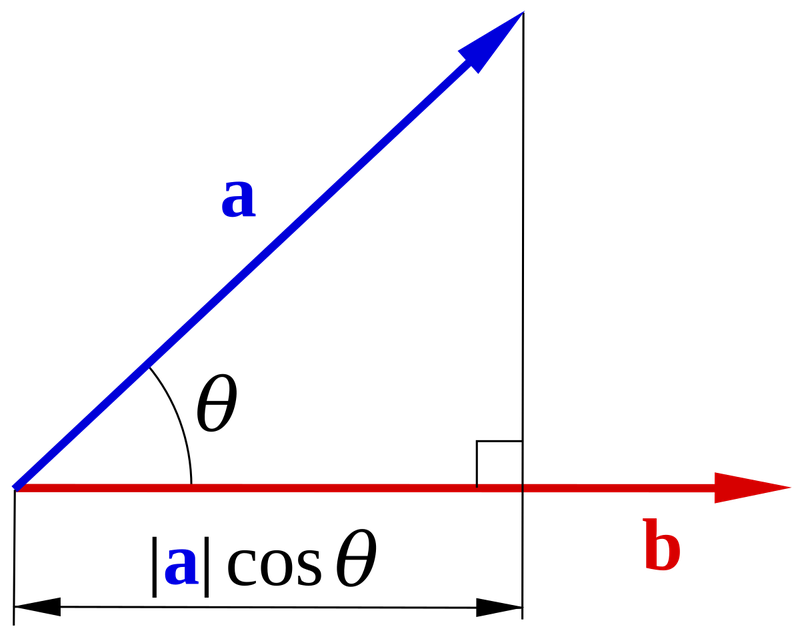
Cho hai vectơ 𝑎 và 𝑏 khác vectơ không (0), tích vô hướng của chúng được định nghĩa bởi công thức:

a.b = IaI.IbI.cos(q)

Trong đó:

• ∣a∣ và ∣b∣ lần lượt là độ dài của hai vectơ 𝑎 và 𝑏.
• θ là góc giữa hai vectơ 𝑎 và 𝑏.

Một cách trực quan, tích vô hướng của hai vectơ đo mức độ tương quan giữa hai vectơ theo hướng của chúng. Nếu hai vectơ cùng hướng, tích vô hướng đạt giá trị lớn nhất; nếu chúng vuông góc, giá trị sẽ bằng 0.

Tích vô hướng của hai vectơ có những tính chất nào?

Tích vô hướng của hai vectơ có một số tính chất quan trọng như:

Tính giao hoán

Tích vô hướng của hai vectơ có tính chất giao hoán, nghĩa là thứ tự của hai vectơ trong phép toán không ảnh hưởng đến kết quả. Công thức biểu diễn tính chất này là:

• a.b=b.a

Điều này xuất phát từ công thức tổng quát của tích vô hướng:

• a.b=∣a∣∣b∣cos(θ)

Trong đó θ là góc giữa hai vectơ 𝑎 và 𝑏. Vì phép toán nhân số thực có tính giao hoán và cos(θ) không bị ảnh hưởng bởi thứ tự của hai vectơ, nên tích vô hướng của hai vectơ cũng có tính giao hoán.

Tính phân phối

Tích vô hướng có tính chất phân phối đối với phép cộng vectơ. Cụ thể, với ba vectơ 𝑎, 𝑏, 𝑐, ta có:

• a.(b+c)=a.b+a.c

Điều này có nghĩa là nếu một vectơ nhân với tổng của hai vectơ khác, thì kết quả bằng tổng của các tích vô hướng tương ứng.

Biểu thức tọa độ của tích vô hướng

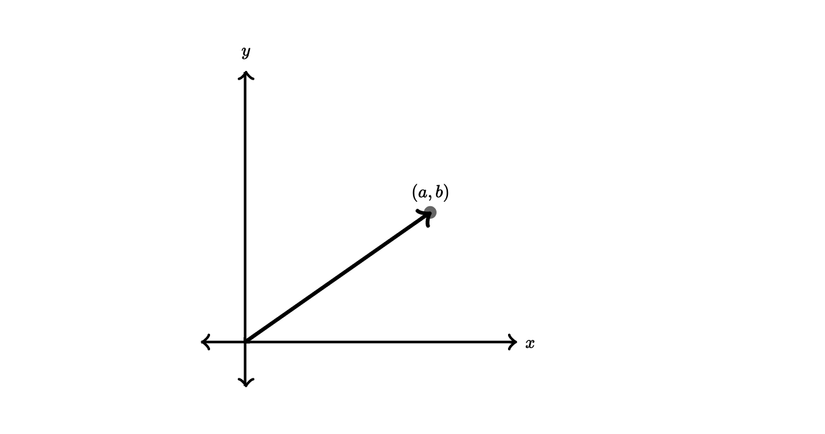
Trong hệ tọa độ Descartes, nếu hai vectơ được biểu diễn dưới dạng:

Các ứng dụng thực tế tích vô hướng của hai vectơ

Xác định góc giữa hai vectơ

Một trong những ứng dụng quan trọng nhất của tích vô hướng của hai vectơ là giúp xác định góc giữa chúng. Công thức tính góc giữa hai vectơ dựa trên tích vô hướng là:

cos(θ)= (∣u∣∣v∣)/(u.v)

Khi hai vectơ có góc nhỏ hơn 90 độ, giá trị cos(θ) dương, cho thấy hai vectơ có xu hướng cùng chiều. Khi góc lớn hơn 90 độ, giá trị cos(θ) âm, nghĩa là hai vectơ có xu hướng ngược chiều. Nếu góc là 90 độ, cos(θ) bằng 0, cho thấy hai vectơ vuông góc với nhau.

Ứng dụng của công thức này rất phổ biến trong đồ họa máy tính, xử lý ảnh và trí tuệ nhân tạo. Ví dụ, trong thị giác máy tính, khi nhận diện hình ảnh, ta có thể sử dụng tích vô hướng của hai vectơ để xác định góc giữa các đường viền của đối tượng, từ đó phân loại hình dạng hoặc phát hiện vật thể trong ảnh.

Trong thực tế, thuật toán dò tìm vật thể trong ảnh (Object Detection) sử dụng nguyên lý này để so sánh hướng và góc giữa các cạnh hoặc biên của một vật thể với các mẫu có sẵn trong cơ sở dữ liệu. Điều này giúp cải thiện độ chính xác khi phân loại và nhận diện hình ảnh.

Kiểm tra tính vuông góc

Trong toán học, một phương pháp đơn giản để kiểm tra xem hai vectơ có vuông góc hay không là tính tích vô hướng của hai vectơ. Nếu kết quả bằng 0, tức là: u.v=0 thì hai vectơ đó vuông góc với nhau.

Ứng dụng của phương pháp này rất phổ biến trong hình học không gian và vật lý. Ví dụ, trong phân tích chuyển động của vật thể, người ta sử dụng nguyên lý này để kiểm tra xem một vật thể có đang di chuyển theo phương vuông góc với một lực tác dụng nào đó hay không. 

Trong kỹ thuật, phép kiểm tra này giúp xác định xem hai bề mặt có vuông góc với nhau hay không, điều này rất quan trọng trong thiết kế cơ khí và xây dựng.

Một ví dụ cụ thể khác là trong lĩnh vực điều hướng robot, cảm biến điều hướng sẽ kiểm tra xem robot có đang di chuyển theo hướng vuông góc với vật cản hay không để điều chỉnh lộ trình. Nếu tích vô hướng của hai vectơ giữa hướng di chuyển của robot và mặt phẳng vật cản bằng 0, có nghĩa là robot đang di chuyển vuông góc với vật cản và có thể tiếp tục đi thẳng.

Ứng dụng trong đồ họa máy tính

Trong đồ họa máy tính và game 3D, tích vô hướng của hai vectơ đóng vai trò quan trọng trong tính toán ánh sáng và bóng đổ của vật thể. Một ứng dụng tiêu biểu là mô hình chiếu sáng phong (Phong Shading), trong đó ánh sáng phản xạ từ một bề mặt được tính dựa trên tích vô hướng hai vectơ giữa vectơ pháp tuyến của bề mặt và hướng ánh sáng.

Ngoài ra, tích vô hướng của hai vectơ cũng được sử dụng để tính toán phản xạ ánh sáng trong các hiệu ứng đổ bóng, giúp tạo ra hình ảnh chân thực hơn.

Tạm kết

Tích vô hướng của hai vectơ là một công thức quan trọng trong toán học và nhiều lĩnh vực liên quan. Việc hiểu rõ về phép toán này sẽ giúp ích rất nhiều trong các bài toán thực tế cũng như trong nghiên cứu khoa học và công nghệ.

Nếu bạn là học sinh, sinh viên đang tìm kiếm một chiếc laptop phù hợp để học tập thì hãy tham khảo ngay những sản phẩm laptop chất lượng có mức giá tốt tại FPT Shop.

Xem thêm về các sản phẩm laptop học sinh sinh viên giá rẻ tại đây:

• Laptop học sinh

Xem thêm:

• Khám phá định luật Newton là gì? Giải đáp chi tiết về 3 định luật Newton có thể bạn chưa biết
• Cách tính khoảng cách giữa hai đường thẳng trong hình học phẳng và không gian