Cách tính khoảng cách giữa hai đường thẳng trong hình học phẳng và không gian

Trong toán học, khái niệm khoảng cách giữa hai đường thẳng đóng vai trò quan trọng trong việc giải quyết các bài toán hình học từ cơ bản đến nâng cao. Dù bạn đang học về hình học phẳng hay khám phá không gian ba chiều, việc tính toán khoảng cách giữa hai đường thẳng luôn là một kỹ năng cần thiết. Vì vậy, chúng ta hãy cùng tìm hiểu cách tính khoảng cách giữa hai đường thẳng trong hình học phẳng và không gian để bạn có thể áp dụng các phương pháp này trong các tình huống thực tế và trong học tập.

Cách tính khoảng cách giữa hai đường thẳng trong hình học phẳng

Để tính khoảng cách giữa hai đường thẳng trong hình học phẳng, bạn sẽ cần biết đặc điểm và công thức tính.

1. Đặc điểm của hai đường thẳng

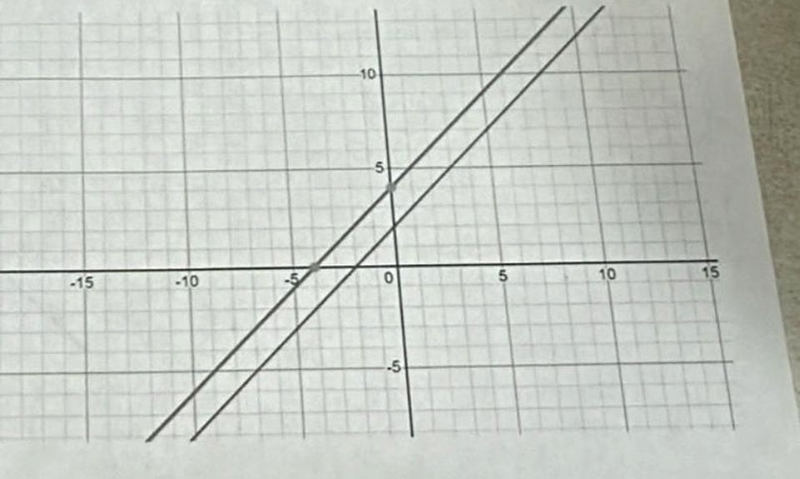
Trong hình học phẳng, hai đường thẳng có thể có ba mối quan hệ chính:

• Song song: Hai đường thẳng song song là khi nó không giao nhau tại bất kỳ điểm nào, tức là các hệ số của x và y trong phương trình tổng quát của nó có cùng tỷ lệ, nhưng hệ số tự do khác nhau. Ví dụ: hai đường thẳng có dạng A_x + B_y + C₁ = 0 và A_x + B_y + C₂ = 0 là song song nếu A/B = A/B, nhưng C₁ ≠ C₂.
• Cắt nhau: Hai đường thẳng cắt nhau khi nó có một điểm giao nhau duy nhất. Điều này xảy ra khi các hệ số của x và y trong phương trình của nó không có cùng tỷ lệ, tức là nếu phương trình của nó có dạng A_x + B_y + C = 0 và A′x + B′y +C′ = 0, thì A/B ≠ A′/B′.
• Trùng nhau: Đây là trường hợp đặc biệt của đường thẳng song song, khi chúng có các hệ số hoàn toàn giống nhau và cùng đi qua mọi điểm.

2. Công thức tính khoảng cách giữa hai đường thẳng song song

Để tính khoảng cách giữa hai đường thẳng song song trong mặt phẳng, bạn có thể sử dụng công thức như sau:

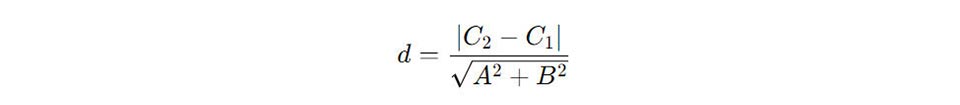
Trong đó:

• A và B là các hệ số của x và y trong phương trình tổng quát của hai đường thẳng.
• C_1​ và C₂​ là các hệ số tự do của hai đường thẳng song song.

Ví dụ: với hai đường thẳng 3x + 4y + 5 = 0 và 3x + 4y – 7 = 0, khoảng cách giữa 2 đường thẳng này sẽ được tính là:

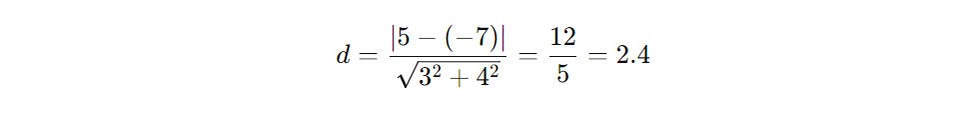
Điều này cho thấy khoảng cách giữa hai đường thẳng song song thực chất là khoảng cách vuông góc từ một điểm bất kỳ trên một đường thẳng tới đường thẳng còn lại​.

3. Cách tính khoảng cách giữa hai đường thẳng cắt nhau

Đối với hai đường thẳng cắt nhau, không có khoảng cách cố định giữa chúng vì chúng giao nhau tại một điểm duy nhất. Tuy nhiên, trong trường hợp cần xác định khoảng cách từ một điểm trên một đường thẳng đến đường thẳng còn lại (không phải tại điểm giao nhau), bạn có thể áp dụng công thức tính khoảng cách từ điểm đến đường thẳng:

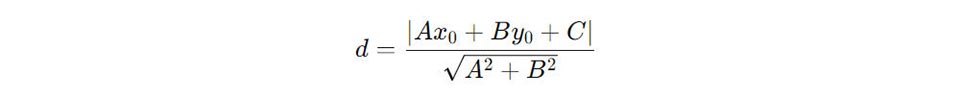
Trong đó:

• A, B, C là hệ số của phương trình đường thẳng.
• (x₀, y₀) là tọa độ của điểm trên đường thẳng kia.

Cách tính khoảng cách giữa hai đường thẳng trong không gian

Tương tự, để biết cách tính khoảng cách giữa hai đường thẳng trong không gian, bạn cần biết hiểu phương pháp phân biệt giữa các đường thẳng song song, cắt nhau và chéo nhau, từ đó áp dụng công thức phù hợp để tính toán.

1. Phân biệt giữa đường thẳng song song, cắt nhau và chéo nhau

Dưới đây là một vài gợi ý đơn giản để giúp bạn có thể phân biệt giữa đường thẳng song song, cắt nhau và chéo nhau trong không gian:

• Đường thẳng song song: Trong không gian, hai đường thẳng song song không bao giờ giao nhau và khoảng cách giữa chúng luôn cố định. Chúng có cùng phương và không cùng vị trí.
• Đường thẳng cắt nhau: Hai đường thẳng cắt nhau là khi chúng giao nhau tại một điểm duy nhất trong không gian. Trường hợp này không cần tính khoảng cách vì điểm giao chính là khoảng cách bằng 0.
• Đường thẳng chéo nhau: Hai đường thẳng chéo nhau là khi chúng không nằm trong cùng một mặt phẳng và không giao nhau. Khoảng cách giữa chúng được tính thông qua đoạn vuông góc chung giữa hai đường.

2. Công thức tính khoảng cách giữa hai đường thẳng song song

Khoảng cách giữa hai đường thẳng song song trong không gian có thể được tính tương tự như trong mặt phẳng, bằng công thức:

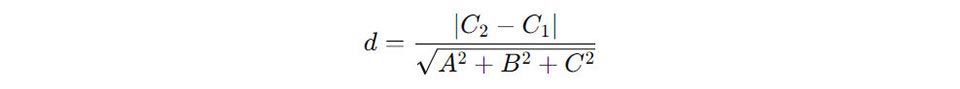
Trong đó:

• A, B, C là hệ số của phương trình tổng quát của hai đường thẳng song song.
• C₁, C₂​ là hệ số tự do trong phương trình của hai đường thẳng.

3. Công thức tính khoảng cách giữa hai đường thẳng chéo nhau

Khoảng cách giữa hai đường thẳng chéo nhau trong không gian được tính bằng đoạn vuông góc chung giữa chúng. Cụ thể, trong hệ tọa độ Oxyz, công thức tính khoảng cách giữa hai đường thẳng chéo nhau là:

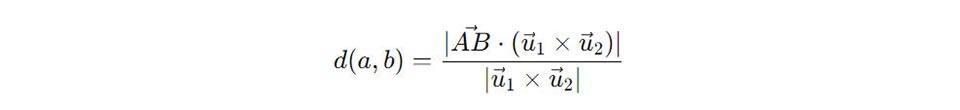
Trong đó:

• u→₁​ và u→₂​ là các vectơ chỉ phương của hai đường thẳng.
• AB→ là vectơ nối từ một điểm trên đường thẳng thứ nhất đến một điểm trên đường thẳng thứ hai.

Dấu “⋅” biểu thị tích vô hướng, còn “×” biểu thị tích có hướng

Phương pháp này giúp bạn dễ dàng tính toán khoảng cách giữa hai đường thẳng chéo nhau bằng cách sử dụng các vectơ và tích có hướng. Nó rất hữu ích trong không gian ba chiều.

Tạm kết

Việc nắm vững cách tính khoảng cách giữa hai đường thẳng trong hình học phẳng và không gian sẽ giúp bạn dễ dàng giải quyết những bài toán học thuật. Ngoài ra, bạn còn có thể áp dụng nó vào các ứng dụng thực tiễn như thiết kế kiến trúc hay nghiên cứu khoa học. Qua bài viết này, FPT Shop hy vọng bạn đã hiểu rõ hơn về các công thức và phương pháp tính để sẵn sàng ứng dụng trong những bài toán phức tạp hơn.

Nếu bạn đang cần mua laptop mới để học tập hoặc làm việc, hãy truy cập vào đường link bên dưới hoặc ghé thăm các cửa hàng gần nhất của FPT Shop nhé.

• Laptop chính hãng

Xem thêm:

• Tổng quan về công thức nguyên hàm và cách ghi nhớ tất cả chỉ trong vài phút
• Tìm hiểu công thức tính công cơ học chuẩn xác và các kiến thức quan trọng nên biết
• Khoảng cách từ 1 điểm đến đường thẳng là gì? Công thức tính toán như thế nào?