Tổng quan về công thức nguyên hàm và cách ghi nhớ tất cả chỉ trong vài phút

Nguyên hàm là khái niệm quan trọng trong giải tích, xuất hiện trong các bài toán học phổ thông và được ứng dụng rộng rãi trong các lĩnh vực như vật lý, kinh tế và khoa học máy tính. Việc hiểu rõ công thức nguyên hàm và cách sử dụng hiệu quả sẽ giúp bạn giải quyết các bài toán tích phân một cách dễ dàng hơn. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về các công thức nguyên hàm cơ bản, cách ghi nhớ chúng và ứng dụng vào việc giải toán.

Nguyên hàm là gì?

Trước khi đi sâu vào công thức nguyên hàm, chúng ta hãy tìm hiểu nguyên hàm là gì. Nguyên hàm của một hàm số là một hàm số khác mà đạo hàm của nó bằng với hàm số ban đầu. Nói cách khác, nếu hàm số F(x) là nguyên hàm của f(x), thì: F′(x)=f(x).

Nguyên hàm đóng vai trò rất quan trọng trong việc tính tích phân. Một trong những ứng dụng phổ biến nhất của nguyên hàm là tìm diện tích dưới đường cong của một hàm số trên một đoạn nhất định.

Tổng hợp các công thức nguyên hàm cơ bản

Để giải quyết tốt các dạng bài toán liên quan đến nguyên hàm, bạn cần ghi nhớ và nắm vững các công thức nguyên hàm cơ bản sau:

Những công thức nguyên hàm trên là cơ bản và rất quan trọng. Bạn có thể gặp chúng thường xuyên trong các bài toán tính tích phân hoặc khi giải các bài toán liên quan đến đạo hàm ngược.

Cách ghi nhớ công thức nguyên hàm một cách hiệu quả

Việc ghi nhớ các công thức nguyên hàm không phải lúc nào cũng dễ dàng, đặc biệt khi bạn phải đối mặt với nhiều công thức khác nhau. Dưới đây là một số mẹo giúp bạn ghi nhớ công thức nhanh chóng và hiệu quả:

• Sử dụng sơ đồ tư duy: Bạn hãy vẽ các sơ đồ tư duy phân loại các công thức nguyên hàm theo các nhóm khác nhau như nhóm hàm đa thức, nhóm hàm lượng giác, nhóm hàm mũ. Điều này giúp bạn dễ dàng hệ thống kiến thức và tìm kiếm nhanh hơn khi cần.
• Luyện tập thường xuyên: Việc thực hành các bài tập thường xuyên là cách tốt nhất để ghi nhớ công thức lâu dài. Bạn có thể chọn các bài toán từ cơ bản đến nâng cao để áp dụng các công thức nguyên hàm và kiểm tra lại khả năng ghi nhớ của mình.
• Sử dụng mẹo ghi nhớ: Đối với những công thức phức tạp, bạn có thể sáng tạo ra các câu thơ, câu văn hoặc các cách ghi nhớ vui nhộn để giúp bạn dễ dàng gợi nhớ lại trong các kỳ thi.

Ứng dụng công thức nguyên hàm trong các dạng bài toán

Một khi đã nắm vững các công thức nguyên hàm, bạn có thể áp dụng chúng vào việc giải quyết các bài toán tích phân cũng như các bài toán liên quan. Dưới đây là một số dạng bài toán phổ biến mà công thức nguyên hàm thường được sử dụng:

1. Tính tích phân xác định và không xác định

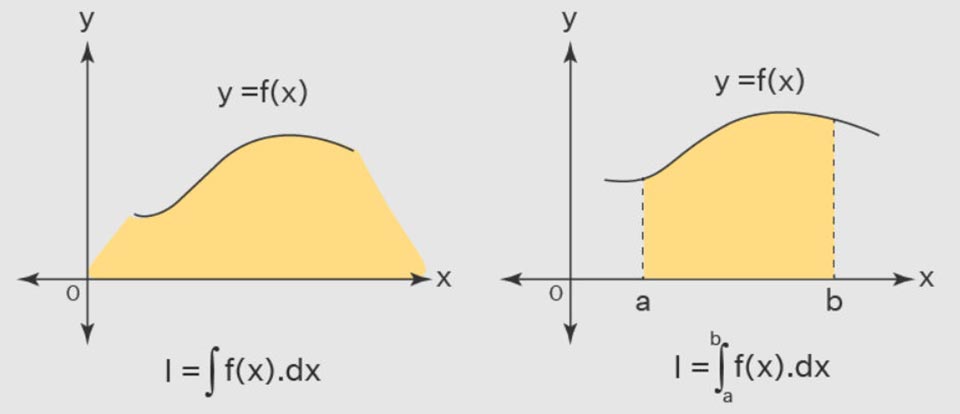
Một trong những ứng dụng phổ biến nhất của nguyên hàm là tính tích phân. Trong đó, tích phân xác định thường được dùng để tính toán diện tích dưới đồ thị của một hàm số trên một khoảng nhất định. Đây là công cụ quan trọng trong toán học, giúp bạn xác định tổng giá trị liên tục của một hàm trên một đoạn, chẳng hạn như khi tính diện tích hình học hoặc khối lượng. Còn tích phân không xác định giúp tìm ra hàm số nguyên thủy của một hàm số đã cho.

2. Giải phương trình vi phân

Việc giải phương trình vi phân thường yêu cầu tính toán các nguyên hàm của các hàm số đã cho. Bằng cách sử dụng công thức nguyên hàm, ta có thể tìm ra hàm số tổng quát của nghiệm và giải được phương trình vi phân đó. Điều này rất quan trọng trong nhiều bài toán liên quan đến động lực học, dòng chảy chất lỏng, điện học và nhiệt động lực học.

3. Tính toán trong vật lý và kỹ thuật

Nguyên hàm đóng vai trò thiết yếu trong việc mô hình hóa các hiện tượng vật lý. Các bài toán về động lực học, điện từ học, cơ học lượng tử đều yêu cầu tính nguyên hàm để xác định các đại lượng liên quan như vận tốc, vị trí, gia tốc và năng lượng. Ví dụ, khi tính vận tốc từ gia tốc hoặc tính vị trí từ vận tốc, ta cần sử dụng các công thức nguyên hàm. Ngoài ra, nguyên hàm còn được sử dụng để giải quyết các bài toán liên quan đến nhiệt động học, trong đó nhiệt độ thay đổi theo thời gian hoặc theo vị trí.

4. Ứng dụng trong kinh tế và tài chính

Trong lĩnh vực kinh tế, nguyên hàm được sử dụng để mô hình hóa và phân tích các yếu tố kinh tế như sản xuất, tiêu dùng và chi phí. Các bài toán liên quan đến tối ưu hóa chi phí, lợi nhuận hoặc phân tích sản lượng đều cần đến việc tính toán nguyên hàm. Một ứng dụng phổ biến khác trong tài chính là tính giá trị hiện tại của một dòng tiền trong tương lai. Khi tính toán giá trị hiện tại ròng (NPV) hoặc xác định lãi suất liên tục, việc tích phân các giá trị tài chính theo thời gian trở nên quan trọng. 

Công thức nguyên hàm giúp tính toán các bài toán về dòng tiền liên tục, hỗ trợ các nhà kinh tế và nhà đầu tư đưa ra những quyết định chính xác hơn, đây là công thức có tính ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và đời sống.

Tạm kết

Việc nắm vững công thức nguyên hàm là điều quan trọng để giải quyết các bài toán liên quan đến tích phân và đạo hàm ngược. Với kiến thức về nguyên hàm và các công thức cơ bản, bạn sẽ dễ dàng hơn trong việc xử lý các bài toán từ đơn giản đến phức tạp.

Nếu bạn đang có nhu cầu mua một chiếc laptop chất lượng để phục vụ cho công việc của mình, hãy truy cập ngay đường link bên dưới hoặc ghé thăm các cửa hàng của FPT Shop nhé.

• Laptop chính hãng

Xem thêm:

• TOP 8 trang web tính đạo hàm, công thức toán học online miễn phí, chính xác nhất
• 3 cách viết công thức toán học trong Word đơn giản, hiệu quả mà bạn không nên bỏ qua