Tam giác đồng dạng là gì? Tiêu chí xác định, cách nhận biết và ứng dụng trong toán hình học

Tam giác đồng dạng là một khái niệm thường thấy trong toán hình học. Nếu bạn đang tìm hiểu về tam giác đồng dạng, có thể xem ngay bài viết dưới đây. Bên cạnh khái niệm, các tiêu chí xác định tam giác đồng dạng, FPT Shop còn đề cập đến những ứng dụng thực tế của tam giác đồng dạng trong đo đạc, xây dựng và giải quyết các bài toán hình học. Bằng cách nắm vững khái niệm này, người học có thể áp dụng để tính toán độ dài, xác định tỉ lệ và chứng minh các mối quan hệ hình học một cách chính xác.

Giới thiệu về tam giác đồng dạng

Trong hình học, tam giác đồng dạng là một khái niệm quan trọng được ứng dụng rộng rãi cả trong toán học lý thuyết và thực tiễn cuộc sống. 

Hai tam giác được xem là đồng dạng khi và chỉ khi chúng thỏa mãn hai điều kiện: các góc tương ứng phải bằng nhau và độ dài các cạnh tương ứng phải tỉ lệ thuận với nhau. Chính nhờ đặc điểm này, tam giác đồng dạng giúp chúng ta dễ dàng xác định được mối quan hệ giữa các kích thước và góc độ của hai tam giác, ngay cả khi chúng không hoàn toàn giống nhau về kích thước tuyệt đối.

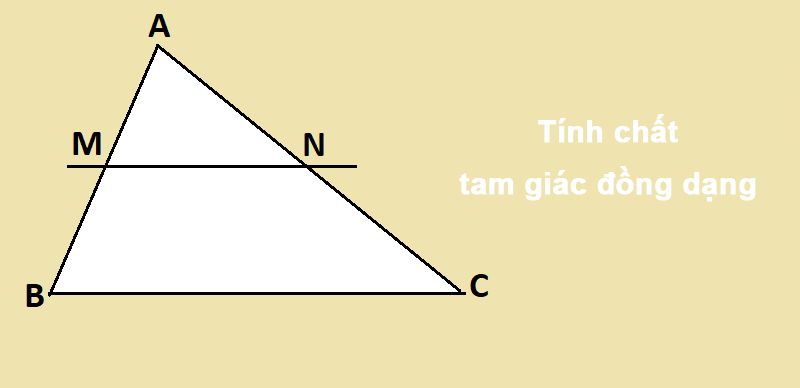
Khi nghiên cứu về tam giác đồng dạng, chúng ta thường tập trung vào các tiêu chí xác định hai tam giác có đồng dạng hay không. Có ba tiêu chí chính thường được sử dụng, bao gồm tiêu chí góc - góc (AA), cạnh - góc - cạnh (SAS), và cạnh - cạnh - cạnh (SSS). Các tiêu chí này là cơ sở để chứng minh đồng dạng trong các bài toán hình học, giúp học sinh và các nhà nghiên cứu giải quyết những bài toán phức tạp một cách hiệu quả.

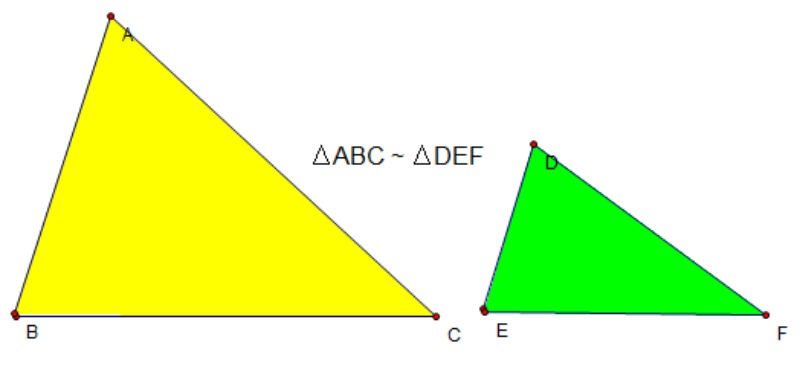
Bên cạnh đó, tam giác đồng dạng còn đóng vai trò quan trọng trong thực tiễn đời sống. Người ta áp dụng nguyên lý này để đo chiều cao của các công trình kiến trúc, tính toán khoảng cách trong kỹ thuật đo đạc, xây dựng mô hình thu nhỏ trong kiến trúc, và cả trong thiên văn học để đo khoảng cách giữa các thiên thể. Nhờ những ứng dụng đa dạng này, tam giác đồng dạng luôn là một phần thiết yếu của hình học hiện đại.

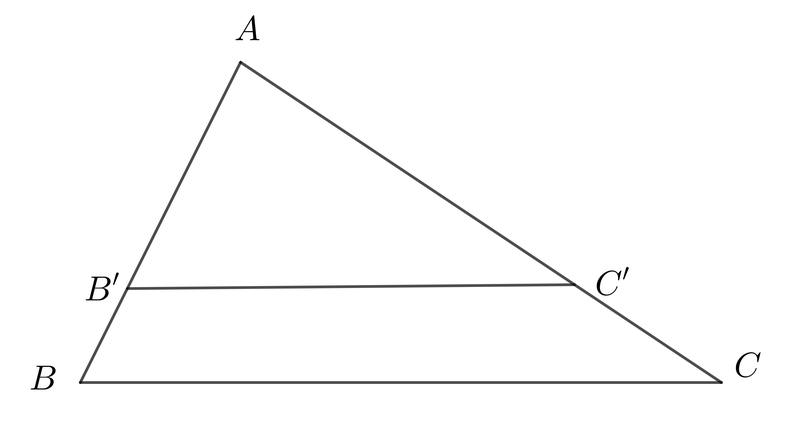
Các tiêu chí xác định tam giác đồng dạng

Có ba tiêu chí chính để xác định hai tam giác có đồng dạng hay không:

Tiêu chí Góc - Góc (AA)

Hai tam giác đồng dạng nếu chúng có hai góc tương ứng bằng nhau. Khi đó, góc thứ ba cũng sẽ bằng nhau do tổng ba góc trong một tam giác luôn bằng 180°.

Tiêu chí Cạnh - Cạnh - Cạnh (SSS)

Hai tam giác đồng dạng nếu ba cặp cạnh của chúng tỉ lệ với nhau.

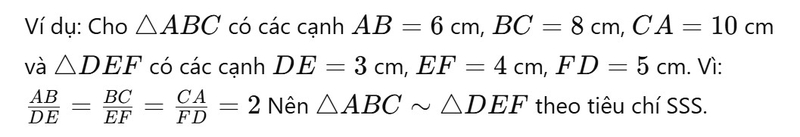
Tiêu chí Cạnh - Góc - Cạnh (SAS)

Hai tam giác đồng dạng nếu chúng có một góc bằng nhau và hai cặp cạnh kề góc đó tỉ lệ với nhau.

Ứng dụng của tam giác đồng dạng

Tính toán độ dài cạnh

Sử dụng tính chất tam giác đồng dạng, ta có thể tính toán độ dài các đoạn thẳng mà không cần đo trực tiếp.

Chứng minh các hệ thức hình học

Tam giác đồng dạng giúp chứng minh các hệ thức tỉ lệ trong hình học.

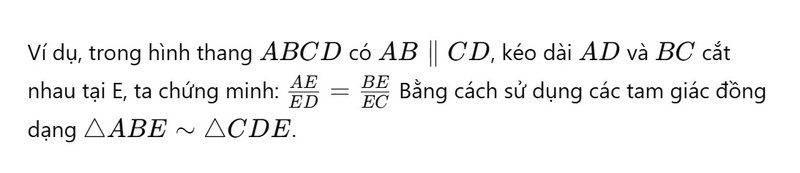
Ứng dụng tam giác đồng dạng trong đo chiều cao của các vật thể

Một trong những ứng dụng phổ biến nhất của tam giác đồng dạng là đo chiều cao các vật thể khó tiếp cận trực tiếp như cây cao, tháp, tòa nhà hoặc núi non. Nguyên lý này được áp dụng dựa trên hiện tượng tạo bóng và tỉ lệ các đoạn thẳng tương ứng.

Giả sử bạn muốn đo chiều cao một tòa nhà cao tầng. Bạn không thể leo lên đỉnh tòa nhà để đo trực tiếp. Khi đó, bạn có thể sử dụng một cây cột có chiều cao đã biết trước, đo chiều dài bóng của cột và bóng của tòa nhà. Sau đó, áp dụng nguyên lý tam giác đồng dạng để tính toán chiều cao tòa nhà. Đây là phương pháp đơn giản, tiết kiệm và rất chính xác trong thực tế.

Tam giác đồng dạng trong xây dựng và kiến trúc

Trong kiến trúc và xây dựng, các kỹ sư thường sử dụng nguyên tắc tam giác đồng dạng để tạo ra các bản vẽ thu nhỏ của công trình xây dựng, hay còn gọi là mô hình kiến trúc. Điều này giúp họ dễ dàng quan sát và chỉnh sửa trước khi thực hiện công trình thật.

Khi thiết kế mô hình, tỉ lệ giữa các kích thước trên mô hình và kích thước thực tế được duy trì nhất quán. Ví dụ, tỉ lệ 1:100 nghĩa là mỗi đơn vị trên mô hình tương ứng với 100 đơn vị trong thực tế. Nguyên lý tam giác đồng dạng sẽ đảm bảo rằng các góc và cạnh vẫn giữ nguyên tỉ lệ khi phóng to lên công trình thực tế.

Tam giác đồng dạng trong lập bản đồ và địa lý

Bản đồ là một ứng dụng điển hình của nguyên lý tam giác đồng dạng. Các bản đồ địa lý được xây dựng theo một tỷ lệ nhất định so với kích thước thực tế. Các tam giác được sử dụng để thể hiện khoảng cách, vị trí địa lý theo tỷ lệ chuẩn.

Ví dụ, trên một bản đồ ghi tỉ lệ 1:10.000, mỗi cm trên bản đồ tương đương với 10.000 cm (100 m) ngoài thực địa. Tỉ lệ này được xây dựng dựa trên nguyên lý tam giác đồng dạng để giữ đúng tương quan kích thước và khoảng cách.

Ứng dụng tam giác đồng dạng trong nhiếp ảnh và quay phim

Trong kỹ thuật nhiếp ảnh và điện ảnh, các nhiếp ảnh gia thường sử dụng tam giác đồng dạng để xác định khoảng cách phù hợp giữa máy ảnh và vật thể, đảm bảo khung hình đẹp, đúng tỉ lệ.

Ví dụ, khi quay phim hoặc chụp ảnh chân dung, người chụp xác định khoảng cách từ máy ảnh đến người mẫu dựa vào tỉ lệ của tam giác đồng dạng, giúp đạt được góc quay và kích thước lý tưởng.

Ứng dụng tam giác đồng dạng trong kỹ thuật cầu đường

Kỹ sư cầu đường sử dụng nguyên lý tam giác đồng dạng để thiết kế và xây dựng các cầu đường, đặc biệt trong việc xác định kích thước của dầm cầu hoặc độ dốc của đường. Bằng cách tính toán dựa trên tỉ lệ đồng dạng, các kỹ sư có thể xây dựng những công trình đảm bảo độ bền và an toàn.

Tạm kết

Tam giác đồng dạng là khái niệm quan trọng trong hình học và có nhiều ứng dụng thực tiễn trong đo đạc, kiến trúc và tính toán khoảng cách. Việc hiểu rõ các tiêu chí đồng dạng giúp chúng ta dễ dàng giải quyết các bài toán hình học cũng như áp dụng thực tế. Mong rằng những gì FPT Shop vừa chia sẻ về tam giác đồng dạng sẽ hữu ích với bạn.

Để học tập tốt hơn và tận dụng công nghệ trong việc nghiên cứu toán học, một chiếc laptop phù hợp là điều không thể thiếu. Nếu bạn đang tìm kiếm laptop học sinh, sinh viên giá tốt, chính hãng, chất lượng cao, hãy tham khảo ngay những sản phẩm tại FPT Shop để có lựa chọn phù hợp với nhu cầu học tập và làm việc của mình!

Xem thêm về các sản phẩm laptop học sinh sinh viên giá rẻ ở đây:

• Laptop sinh viên giá rẻ

Xem thêm:

• Cách tính chu vi hình tam giác chính xác nhất: Áp dụng cho cả tam giác đều, cân, vuông và thường
• Cách tính diện tích tam giác: Tổng hợp các công thức từ cơ bản đến nâng cao