Bảng công thức nguyên hàm đầy đủ nhất: Công thức cơ bản, nâng cao và phương pháp ghi nhớ hiệu quả

Nguyên hàm là một trong những khái niệm cốt lõi của giải tích, đóng vai trò quan trọng trong việc giải các bài toán tích phân và phương trình vi phân. Không chỉ dừng lại ở lý thuyết, nguyên hàm còn có ứng dụng sâu rộng trong nhiều lĩnh vực khác nhau như vật lý, kỹ thuật, kinh tế hay cả khoa học tự nhiên. Việc nắm vững các tính chất và công thức nguyên hàm không chỉ giúp học sinh, sinh viên giải quyết nhanh các bài toán trên lớp mà còn mở ra cánh cửa để hiểu sâu hơn về cách thế giới vận hành qua lăng kính toán học. Hãy cùng khám phá bảng công thức và tầm quan trọng của nguyên hàm để sẵn sàng chinh phục mọi thử thách trong học tập và thực tiễn!

Nguyên hàm là gì?

Nguyên hàm, một khái niệm quan trọng trong giải tích, có mối liên hệ chặt chẽ với đạo hàm và tích phân. Nếu đạo hàm giúp chúng ta tìm tốc độ thay đổi tức thời thì nguyên hàm là quá trình ngược lại, nhằm xác định hàm số ban đầu từ đạo hàm của nó.

Định nghĩa nguyên hàm: Một hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên một tập hợp K, nếu với mọi x∈K, ta có: F′(x)=f(x)

Vai trò của nguyên hàm trong môn toán học:

• Giải nhanh chóng và chính xác các bài toán tích phân.
• Tính diện tích, thể tích và các bài toán vật lý liên quan đến chuyển động.
• Ứng dụng trong các lĩnh vực kinh tế, kỹ thuật và khoa học tự nhiên.

Lưu ý: Nguyên hàm không phải là duy nhất. Với mỗi hàm f(x), có vô số nguyên hàm khác nhau, khác biệt bởi một hằng số C: F(x)+C.

Trong các phần tiếp theo, chúng ta sẽ khám phá bảng công thức nguyên hàm và cách áp dụng chúng hiệu quả nhất!

Các định lý về nguyên hàm

Định lý 1

Nếu F(x) là một nguyên hàm của hàm số f(x) trên một khoảng K, thì với mỗi hằng số C, hàm số G(x)=F(x)+C cũng là một nguyên hàm của f(x) trên khoảng K.

Ý nghĩa: Nguyên hàm không chỉ có một dạng duy nhất mà tồn tại dưới dạng một họ các hàm số khác nhau, được biểu diễn bằng F(x)+C, trong đó C là hằng số.

Định lý 2

Nếu F(x) là một nguyên hàm của hàm số f(x) trên một khoảng K, thì mọi nguyên hàm của f(x) trên K đều có dạng: F(x)+C,với C là một hằng số.

• Ý nghĩa: Điều này khẳng định rằng họ tất cả các nguyên hàm của f(x) trên khoảng K có thể được biểu diễn bằng công thức chung: F(x)+C, với C∈R (hằng số thực).

Kết luận về định lý

Từ hai định lý trên, ta có thể tổng quát:

• F(x)+C, C∈R, là họ tất cả các nguyên hàm của hàm số f(x) trên khoảng K.
• Việc hiểu và áp dụng định lý này giúp giải các bài toán nguyên hàm và tích phân một cách chính xác hơn.

Tính chất của nguyên hàm

Nguyên hàm tuân theo một số tính chất quan trọng giúp đơn giản hóa việc tính toán trong giải tích. Hiểu rõ tính chất của nguyên hàm giúp bạn dễ dàng giải quyết các bài toán tích phân và áp dụng các công thức một cách hiệu quả. Dưới đây là các tính chất cơ bản của nguyên hàm mà bạn cần ghi nhớ:

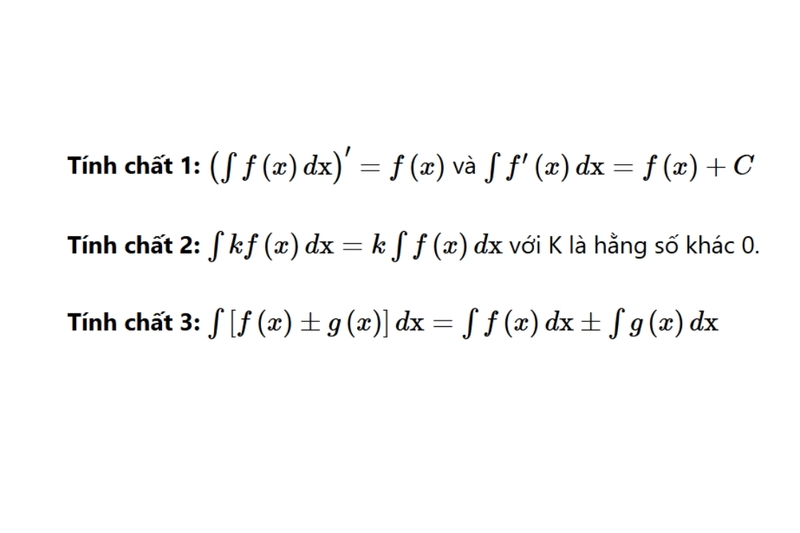
Nhờ các tính chất này, việc phân tích và xử lý các bài toán liên quan đến tích phân trở nên đơn giản hơn. Thay vì phải tính toán phức tạp, bạn chỉ cần áp dụng các tính chất để tách bài toán lớn thành các phần nhỏ và xử lý từng phần.

Trong phần tiếp theo, chúng ta sẽ đi sâu vào bảng công thức nguyên hàm đầy đủ, giúp bạn hệ thống hóa và ghi nhớ các công thức quan trọng!

Bảng công thức nguyên hàm

Bảng công thức nguyên hàm là công cụ không thể thiếu để giải các bài toán tích phân và nguyên hàm trong giải tích. Việc nắm vững các công thức không chỉ giúp bạn giải nhanh các bài toán mà còn hỗ trợ trong việc hiểu sâu hơn về toán học và các ứng dụng thực tế.

• Tính toàn diện: Bao gồm từ công thức cơ bản đến nâng cao.
• Ứng dụng thực tiễn: Hỗ trợ trong các bài toán vật lý, kinh tế và kỹ thuật.

Dưới đây là các công thức cơ bản nhất mà bạn cần nắm vững, hãy lưu bảng công thức này và luyện tập thường xuyên để nắm chắc kiến thức nguyên hàm nhé!

Lưu ý:

• Xác định đúng dạng của hàm số trước khi áp dụng công thức.
• Chú ý các điều kiện của n, a, hoặc các giới hạn trong các công thức đặc biệt.
• Sử dụng các tính chất tuyến tính để tách hàm số phức tạp thành các thành phần đơn giản hơn.

Mẹo ghi nhớ bảng công thức nguyên hàm hiệu quả

Việc ghi nhớ các công thức nguyên hàm có thể trở nên dễ dàng hơn nếu bạn áp dụng các mẹo sau:

Phân nhóm công thức

Hãy chia nhỏ bảng công thức thành các nhóm dễ học và dễ nhớ hơn:

• Nhóm cơ bản: Các công thức như nguyên hàm của hằng số, x^n, e^x, ln⁡x.
• Nhóm lượng giác: Các công thức liên quan đến sin⁡x, cos⁡x, tan⁡x, cot⁡x.
• Nhóm lượng giác ngược và hàm đặc biệt: Các công thức của arcsin⁡x, arccos⁡x, sinh⁡x, cosh⁡x.

Việc học theo nhóm sẽ giúp bạn dễ dàng liên kết và ghi nhớ các công thức có đặc điểm tương đồng.

Luyện tập thường xuyên

• Mỗi công thức hãy đi kèm một bài tập mẫu để hiểu cách sử dụng.
• Mỗi ngày, hãy dành thời gian làm từ 3 đến 5 bài tập liên quan đến các công thức nguyên hàm.
• Kết hợp bài tập từ cơ bản đến nâng cao để hiểu rõ cách áp dụng từng công thức.
• Sau khi làm xong, bạn nên kiểm tra lại lời giải để rút kinh nghiệm.

Sử dụng sơ đồ tư duy

• Tóm tắt các công thức trong một sơ đồ hoặc bảng tổng hợp.
• Vẽ các nhánh sơ đồ liên kết giữa các nhóm công thức, như nhóm cơ bản, lượng giác, đặc biệt.
• Màu sắc hóa sơ đồ để tạo ấn tượng mạnh giúp ghi nhớ lâu hơn.

Tạo quy tắc ghi nhớ hoặc mẹo vần

• Sử dụng các câu thơ, mẹo vần dễ thuộc để ghi nhớ công thức. Ví dụ: “Nguyên hàm sin về cos, cos về sin ngược dấu thôi.”
• Tự sáng tạo các câu vần theo cách bạn cảm thấy dễ nhớ nhất.

Sử dụng ứng dụng hỗ trợ

• Học qua các ứng dụng hỗ trợ toán học như Mathway, Wolfram Alpha.
• Kiểm tra lời giải và tự so sánh cách làm của mình với các bước tính toán tự động.

Học cùng bạn bè hoặc gia sư

• Tạo nhóm học để cùng nhau ôn luyện và giải bài tập.
• Thảo luận để củng cố kiến thức và giải đáp thắc mắc nhanh hơn.

Kiên nhẫn và kiên trì

Việc học nguyên hàm cần thời gian và sự lặp lại. Đừng nản chí nếu bạn chưa ghi nhớ hết ngay lập tức. Hãy tiếp tục luyện tập và ôn tập thường xuyên, bạn sẽ dần ghi nhớ được toàn bộ công thức!

Lời kết

Nguyên hàm, một phần kiến thức cốt lõi của giải tích, không chỉ giúp giải bài toán trong học tập mà còn có vai trò quan trọng trong phân tích các vấn đề thực tiễn. Nắm vững bảng công thức nguyên hàm đòi hỏi sự chăm chỉ và áp dụng các phương pháp học tập hiệu quả.

Hy vọng qua bài viết này, bạn đã có cái nhìn toàn diện hơn về bảng công thức nguyên hàm từ cơ bản đến nâng cao và biết cách ghi nhớ chúng một cách dễ dàng. Hãy bắt đầu từ những bước nhỏ, luyện tập thường xuyên và không ngừng nâng cao kiến thức của mình. Chúc bạn thành công và đạt điểm cao trong các kỳ thi!

Hãy trang bị ngay laptop chính hãng tại FPT Shop để việc học nguyên hàm và giải tích trở nên dễ dàng hơn! Với đa dạng mẫu mã, cấu hình mạnh mẽ và nhiều ưu đãi hấp dẫn dành cho học sinh, sinh viên, FPT Shop là người bạn đồng hành lý tưởng giúp bạn chinh phục mọi bài toán khó. Xem nhanh tại link sau:

• Máy tính xách tay

Xem thêm:

• Bật mí cho bạn các cách tính đạo hàm nhanh chóng và chính xác trong toán học
• TOP 8 trang web tính đạo hàm, công thức toán học online miễn phí, chính xác nhất