Trục đối xứng là gì? Hình nào có trục đối xứng? Hình nào không có trục đối xứng?

Trục đối xứng là một khái niệm cơ bản và quan trọng trong hình học, đặc biệt đối với học sinh cấp 2 và cấp 3. Hiểu rõ về trục đối xứng là gì không chỉ giúp các em nắm vững kiến thức toán học mà còn phát triển tư duy logic và khả năng quan sát hình học trong thực tế.

Trục đối xứng là gì?

Trục đối xứng là gì? Trục đối xứng (tiếng Anh: Line of Symmetry) là đường thẳng d mà khi "gấp" một hình theo đường thẳng này, hai phần của hình sẽ "chồng khít" lên nhau hoàn toàn. Nói cách khác, đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H.

Hai điểm được coi là đối xứng với nhau qua một đường thẳng d khi d là đường trung trực của đoạn thẳng nối giữa hai điểm đó.

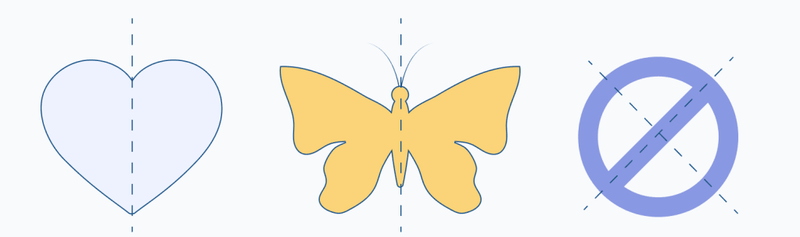
Các hình cơ bản có trục đối xứng là gì?

Đường tròn

Đường tròn là hình có nhiều trục đối xứng nhất. Mọi đường thẳng đi qua tâm đều là trục đối xứng của đường tròn. Do có vô hạn đường thẳng như vậy, hình tròn có vô số trục đối xứng.

Các loại tam giác

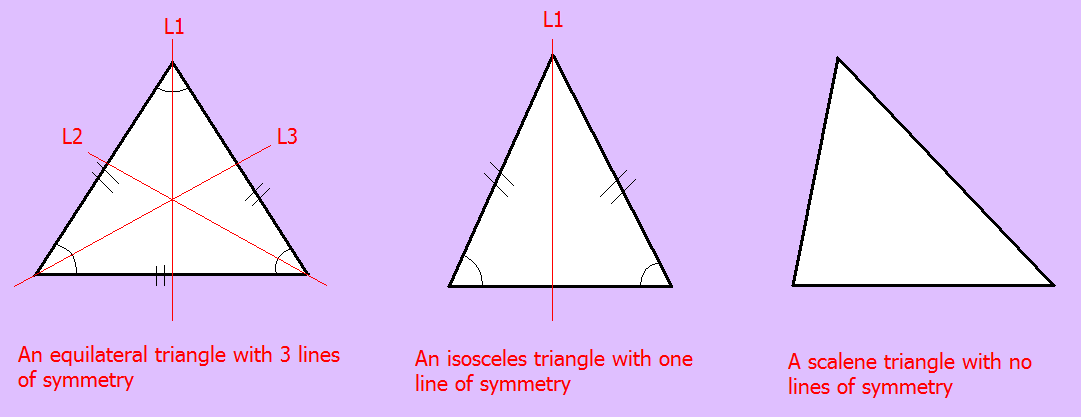
• Tam giác cân: Có một trục đối xứng duy nhất là đường thẳng đi qua đỉnh góc cân và trung điểm của cạnh đáy. Trục này đồng thời là đường cao, đường trung tuyến, đường phân giác và đường trung trực xuất phát từ đỉnh.
• Tam giác đều: Có ba trục đối xứng, mỗi trục đi qua một đỉnh và trung điểm của cạnh đối diện. Các trục này cũng đồng thời là đường cao, đường trung tuyến và đường phân giác.

Các tứ giác đặc biệt

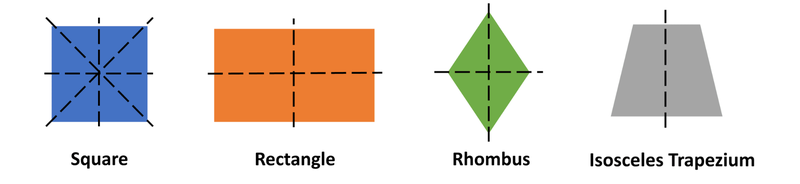
• Hình thang cân: Có một trục đối xứng là đường thẳng đi qua trung điểm của hai đáy. Đây là một định lý quan trọng trong hình học lớp 8.
• Hình thoi: Có hai trục đối xứng là hai đường chéo của hình thoi.
• Hình chữ nhật: Có hai trục đối xứng là các đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện.
• Hình vuông: Có bốn trục đối xứng bao gồm hai đường chéo và hai đường thẳng đi qua trung điểm của mỗi cặp cạnh đối diện.

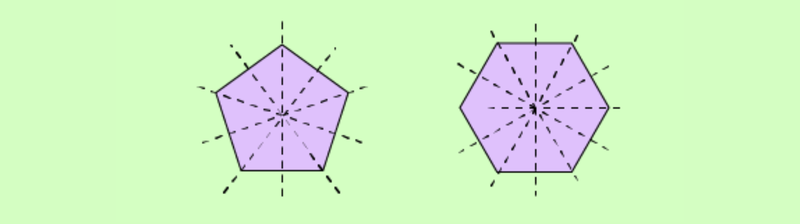
Đa giác đều

Một quy luật quan trọng: Đa giác đều có n cạnh thì có n trục đối xứng. Ví dụ:

• Hình ngũ giác đều có 5 trục đối xứng.
• Hình lục giác đều có 6 trục đối xứng.

Tính chất quan trọng của phép đối xứng trục

Phép đối xứng trục có những tính chất đặc biệt mà học sinh cần nắm vững:

• Bảo toàn khoảng cách: Khoảng cách giữa hai điểm bất kỳ được giữ nguyên sau phép đối xứng
• Biến đường thẳng thành đường thẳng: Đoạn thẳng được biến thành đoạn thẳng bằng nó
• Bảo toàn góc: Góc giữa hai đường thẳng không thay đổi
• Hai hình đối xứng nhau qua một đường thẳng thì bằng nhau

Ứng dụng thực tế của trục đối xứng

Trục đối xứng không chỉ xuất hiện trong sách giáo khoa mà còn có mặt khắp nơi trong cuộc sống:

• Kiến trúc: Các tòa nhà, đền chùa thường được thiết kế theo nguyên tắc đối xứng để tạo sự cân đối và hài hòa.

• Thiết kế: Logo, biểu tượng thường sử dụng tính đối xứng để tạo ấn tượng mạnh.
• Tự nhiên: Lá cây, cánh bướm, khuôn mặt con người đều có tính đối xứng.

Bài tập ví dụ minh họa

Bài tập 1: Xác định số trục đối xứng

Trong các hình sau, mỗi hình có bao nhiêu trục đối xứng?

• Hình tròn: Vô số trục (mọi đường kính)
• Hình chữ nhật: 2 trục (qua trung điểm các cặp cạnh đối diện)
• Tam giác đều: 3 trục (qua mỗi đỉnh và trung điểm cạnh đối diện)
• Hình lục giác đều: 6 trục

Bài tập 2: Tìm trục đối xứng của chữ cái

• Chữ cái có một trục đối xứng dọc: A, M, T, U, V, W, Y
• Chữ cái có một trục đối xứng ngang: B, C, D, E, K
• Chữ cái có hai trục đối xứng: H, I, O, X

Giải đáp một số câu hỏi thường gặp

Tâm đối xứng là gì?

Tâm đối xứng là điểm cố định mà khi quay hình quanh điểm đó 180 độ, hình thu được trùng với hình ban đầu.

Hình nào có trục đối xứng?

Đường tròn: Vô số trục đối xứng (mọi đường kính)

• Tam giác cân: 1 trục đối xứng
• Tam giác đều: 3 trục đối xứng
• Hình thang cân: 1 trục đối xứng
• Hình thoi: 2 trục đối xứng
• Hình chữ nhật: 2 trục đối xứng
• Hình vuông: 4 trục đối xứng

Trục đối xứng của đường tròn là gì?

Trục đối xứng của đường tròn là mọi đường thẳng đi qua tâm (đường kính). Đường tròn có vô số trục đối xứng.

Hình nào không có trục đối xứng?

• Hình bình hành thông thường
• Tam giác thường (không cân, không đều)
• Hình thang thông thường (không cân)

Hình bình hành có trục đối xứng không?

Không, hình bình hành thông thường không có trục đối xứng. Tuy nhiên, hình bình hành có tâm đối xứng tại giao điểm hai đường chéo.

Lưu ý: Hình chữ nhật và hình thoi (là dạng đặc biệt của hình bình hành) có trục đối xứng.

Tạm kết

Qua bài viết này, chắc hẳn bạn đã hiểu rõ trục đối xứng là gì và vai trò của nó trong hình học. Không chỉ giúp giải toán chính xác hơn, khái niệm này còn góp phần rèn luyện tư duy logic và khả năng quan sát hình ảnh một cách trực quan. Việc nắm vững trục đối xứng sẽ là bước đệm quan trọng cho những kiến thức hình học nâng cao và các ứng dụng trong thực tế.

Bạn đang cần một chiếc laptop học tập ổn định để luyện tập các dạng bài toán hình học như trục đối xứng? Hãy đến ngay FPT Shop, nơi cung cấp các dòng laptop học sinh - sinh viên chính hãng từ Dell, ASUS, HP… với hiệu năng tốt, pin bền và giá ưu đãi. Trả góp 0% lãi suất và nhiều quà tặng hấp dẫn đang chờ bạn!

Laptop Sinh viên - Văn phòng

Xem thêm:

• Tam giác đồng dạng là gì? Tiêu chí xác định, cách nhận biết và ứng dụng trong toán hình học
• Trọng tâm tam giác là gì? Tìm hiểu tính chất, công thức tính và bài tập vận dụng