Tổng hợp công thức tính thể tích hình chóp tam giác đều, tứ giác đều và các bài tập minh họa chi tiết

Hiểu rõ cách tính thể tích của các hình chóp sẽ giúp bạn nắm vững kiến thức cơ bản về hình học không gian, áp dụng nó vào các bài toán thực tế một cách hiệu quả. Bài viết này sẽ tập trung vào việc tính thể tích của hai loại hình chóp phổ biến: hình chóp tam giác đều và hình chóp tứ giác đều. Hãy cùng FPT Shop khám phá công thức toán học cần thiết, các bước tính toán chi tiết và ví dụ cụ thể để minh họa quá trình tính toán.

Một số kiến thức cơ bản cần nắm

Hình chóp tam giác đều là gì?

Khái niệm

Hình chóp tam giác đều (còn gọi là hình chóp đều ba diện) là một loại hình chóp có đáy là tam giác đều và các mặt bên là các tam giác đều. Đặc điểm chính của hình chóp tam giác đều là:

• Đáy: Là một tam giác đều, nghĩa là tất cả các cạnh và góc của tam giác này đều bằng nhau.
• Các mặt bên: Là các tam giác đều với một đỉnh chung (đỉnh chóp) và cạnh chung với đáy tam giác.
• Đỉnh chóp: Là điểm chung của tất cả các mặt bên, nằm trên đường thẳng vuông góc với mặt phẳng của đáy tam giác.

Tính chất

• Trục đối xứng: Hình chóp tam giác đều có 3 trục đối xứng.
  • 1 trục đi qua đỉnh và tâm của tam giác đáy.
  • 3 trục đi qua trung điểm của mỗi cạnh đáy và đỉnh.
• Mặt phẳng đối xứng: Hình chóp tam giác đều có 3 mặt phẳng đối xứng.
  • 3 mặt phẳng đi qua mỗi cạnh bên và đường trung tuyến của tam giác đáy

Ứng dụng

Hình chóp tam giác đều thường được sử dụng trong kiến trúc, thiết kế và kỹ thuật. Ví dụ:

• Mái nhà: Một số loại mái nhà có hình dạng chóp tam giác đều.
• Các chi tiết trang trí: Hình chóp tam giác đều thường được sử dụng làm chi tiết trang trí trong kiến trúc và nghệ thuật.
• Các cấu trúc kỹ thuật: Ngoài ra, hình chóp tam giác đều có thể được sử dụng trong các cấu trúc kỹ thuật như tháp, cột...

Hình chóp tứ giác đều là gì?

Khái niệm

Hình chóp tứ giác đều là một hình chóp đặc biệt có các đặc điểm sau:

• Đáy: Là một tứ giác đều, nghĩa là có bốn cạnh bằng nhau và bốn góc bằng nhau (mỗi góc 90 độ).
• Đỉnh: Là điểm nằm trên một đường thẳng vuông góc với mặt phẳng đáy và đi qua tâm của tứ giác đáy.
• Các mặt bên: Là các tam giác cân có chung đỉnh và có đáy là các cạnh của tứ giác đáy.
• Các cạnh bên: Bằng nhau.
• Chiều cao: Là độ dài đường thẳng từ đỉnh xuống tâm của tứ giác đáy.

Tính chất

Hình chóp tứ giác đều là một hình khối đặc biệt với nhiều tính chất thú vị.

• Trục đối xứng: Hình chóp tứ giác đều có 4 trục đối xứng.
  • 1 trục đi qua đỉnh và tâm của tứ giác đáy.
  • 4 trục đi qua trung điểm của mỗi cạnh đáy và đỉnh.
• Mặt phẳng đối xứng: Hình chóp tứ giác đều có 5 mặt phẳng đối xứng.
  • 1 mặt phẳng đi qua đỉnh và trung điểm của hai cạnh đối diện của đáy.
  • 4 mặt phẳng đi qua mỗi cạnh bên và đường trung bình của đáy.
• Chiều cao của hình chóp: Là độ dài đường thẳng vuông góc hạ từ đỉnh xuống tâm của hình vuông đáy.
• Đường cao của mỗi mặt bên: Là đường cao của tam giác cân, đồng thời là trung tuyến của tam giác đó.
• Góc ở đỉnh: Là góc tạo bởi hai cạnh bên.
• Góc ở đáy: Là góc tạo bởi một cạnh bên và một cạnh đáy.
• Mối quan hệ giữa các yếu tố: Chiều cao của hình chóp, cạnh đáy và cạnh bên có mối quan hệ với nhau thông qua định lý Pitago.

Công thức tính thể tích hình chóp tam giác đều

Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng (1/3) diện tích đáy nhân với chiều cao. Cụ thể, bạn có thể áp dụng công thức tính toán như sau:

V = (1/3) x (S x h)

Trong đó:

• V: chính là thể tích của hình chóp tam giác đều.
• S: là diện tích đáy.
• H: là chiều cao.

Ví dụ minh họa:

Tính thể tích hình chóp tam giác đều biết chiều cao của hình chóp là 3 cm, tam giác đáy có cạnh bằng 7 cm và chiều cao bằng (7√3)/2 cm.

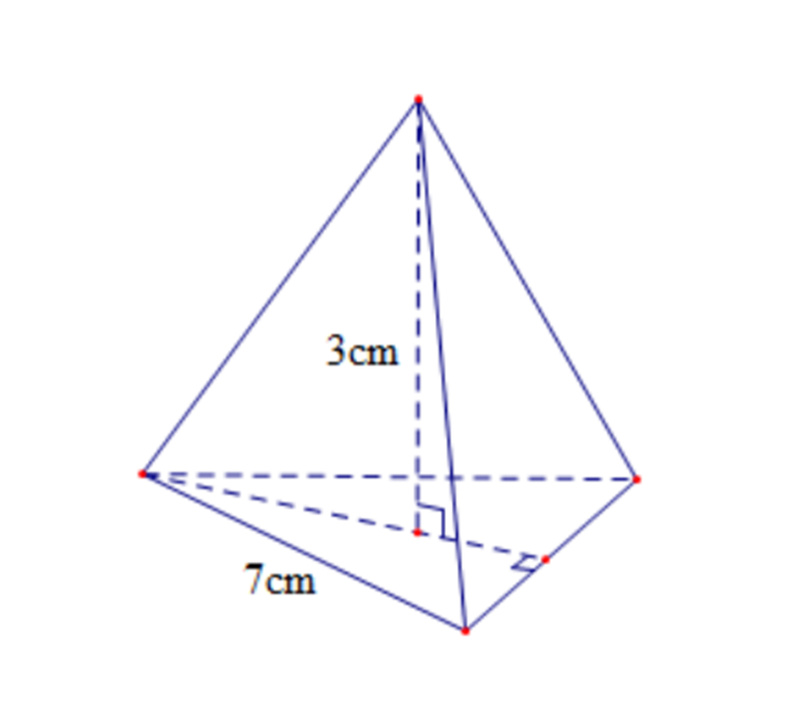
Bài giải:

Diện tích đáy của hình chóp tam giác đều là:

S = (1/2) x 7 x 7√32 = (49√3)/4 (cm²).

Thể tích hình chóp tam giác đều đã cho là:

V= (1/3)  x (S x h) = (1/3) x 49√34 x 3 = 49√34 (cm³).

Cách tính thể tích hình chóp tứ giác đều

Thể tích của hình chóp tứ giác đều bằng (1/3) tích của diện tích mặt đáy với chiều cao của nó. Cụ thể:

V= (1/3) x S x h

Trong đó:

• S: diện tích đáy.
• h: chiều cao của hình chóp.

Ví dụ minh họa:

Tính thể tích của hình chóp tứ giác đều S.ABCD, biết độ dài cạnh đáy bằng 6 cm, chiều cao bằng 4 cm, trung đoạn bằng 5 cm.

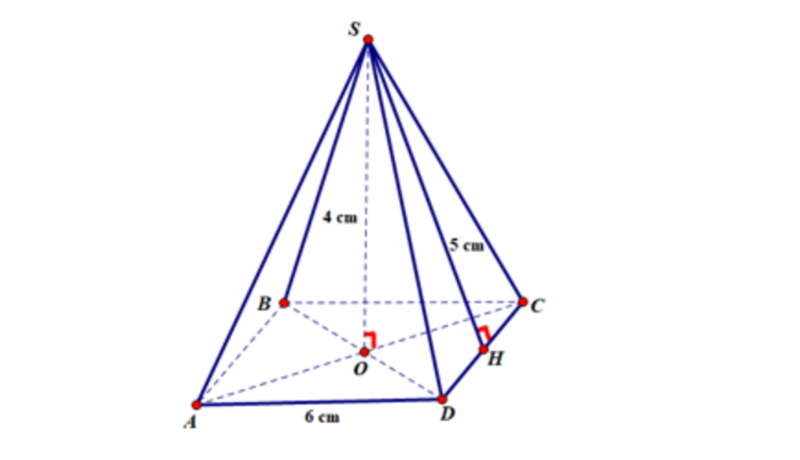
Bài giải:

Diện tích đáy ABCD là: S = 6² = 36 (cm²).

Thể tích của hình chóp tứ giác đều S.ABCD là:

V= (1/3) x S x h = (1/3) x 36 x 4 = 48(cm³).

Vậy thể tích của hình chóp tứ giác đều S.ABCD là 48 cm³.

Những bài tập liên quan đến cách tính thể tích hình chóp

Bài tập có hướng dẫn

Bài tập 1: Tính thể tích hình chóp tam giác đều có cạnh đáy dài 6 cm và chiều cao 10 cm.

Cách giải:

Vì đáy là tam giác đều có cạnh dài a = 6 cm, ta tính diện tích đáy bằng công thức:

S =  (a² √3)/4  = (36√3)/4  = (36√3)/4 = 9√3 cm².

Tính thể tích hình chóp tam giác đều:

V = (1/3) x (S x h).

Với S = 9√3 cm² và h = 10 cm, ta tính được kết quả như sau:

V = (1/3) x 9√3 x 10 = 30√3 cm³.

Bài tập 2: Tính thể tích hình chóp tứ giác đều có chiều cao 5 cm, độ dài cạnh của tứ giác đáy là 8 cm.

Cách giải:

Thể tích hình chóp tứ giác đều đã cho là:

V= (1/3) x S x h = (1/3) x 64 x 5 = 3203 (cm³).

Bài tập tự luyện

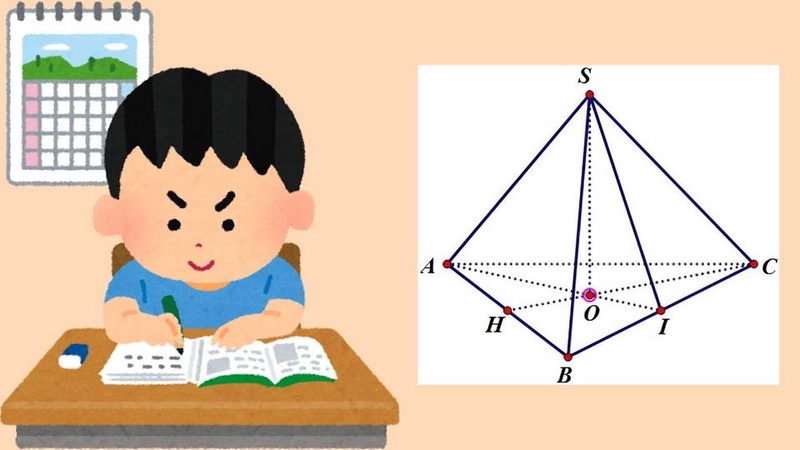
Bài 1: Xét một hình chóp tam giác đều có cạnh đáy là 4 cm và chiều cao của hình chóp là 6 cm. Hãy tính thể tích của hình chóp này.

Bài 2: Tính thể tích của một hình chóp tam giác đều, biết rằng cạnh đáy của nó là 5 cm và đường cao từ đỉnh chóp tới mặt đáy là 10 cm.

Bài 3: Hãy xác định thể tích của một hình chóp tam giác đều với cạnh đáy 6 cm và chiều cao 9 cm.

Bài 4: Cho hình chóp tứ giác đều S.ABCD với AB = a và chiều cao SO = h. Tính thể tích khối chóp.

Bài 5: Cho hình chóp tứ giác đều S.ABCD biết AD = 25mm, SO = 27mm. Tính thể tích hình chóp tứ giác đều S.ABCD ?

Bài 6: Tính chiều cao AH của hình chóp tứ giác đều A.MNPQ biết độ dài cạnh đáy hình vuông MNPQ là 8cm và thể tích của hình chóp tứ giác đều đó là 192 cm³?

Tạm kết

Tính thể tích hình chóp tam giác đều và tứ giác đều là một dạng toán cơ bản nhưng lại có nhiều ứng dụng trong thực tiễn. Bằng cách nắm vững công thức và hiểu rõ các tính chất của hai loại hình chóp này, chúng ta có thể dễ dàng tính toán thể tích của chúng trong các bài toán hình học, kiến trúc, kỹ thuật và nhiều lĩnh vực khác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về chủ đề này.

Bạn đang tìm kiếm một loại máy tính xách tay đáng tin cậy, hiệu suất cao để hỗ trợ quá trình học tập của mình? FPT Shop mang đến cho bạn những máy tính xách tay hàng đầu thị trường với tính năng mạnh mẽ, thiết kế hiện đại và giá cả phải chăng. Hãy ghé thăm FPT Shop ngay hôm nay để khám phá và chọn mua máy tính xách tay phù hợp nhất cho mình.

• Máy tính xách tay

Xem thêm:

• Công thức tính thể tích hình cầu, các dạng bài tập và các ứng dụng hữu ích trong cuộc sống
• Công thức tính thể tích khối chóp: Ví dụ minh hoạ và ứng dụng trong thực tế