Công thức tính thể tích khối chóp: Ví dụ minh hoạ và ứng dụng trong thực tế

Thể tích khối chóp là một trong những kiến thức quan trọng của hình học không gian và được ứng dụng rộng rãi trong nhiều lĩnh vực. Đến với bài viết hôm nay, FPT Shop sẽ giải thích chi tiết công thức tính thể tích khối chóp và minh họa bằng các ví dụ cụ thể. Bạn có thể theo dõi để tìm hiểu công thức, tầm quan trọng của việc tính thể tích khối chóp trong đời sống hiệu quả.

Thể tích là gì?

Thể tích là khái niệm dùng để đo không gian mà một vật thể chiếm giữ trong không gian ba chiều. Nó phản ánh khả năng chứa đựng của vật thể đó. Việc xác định thể tích không chỉ là yêu cầu học thuật mà còn là nền tảng cho các ứng dụng trong thực tế như tính toán vật liệu xây dựng hoặc dung tích các bình chứa. Đơn vị đo thể tích phổ biến gồm:

• Mét khối (m³): Thường dùng để đo các vật thể lớn như bể chứa nước hoặc phòng ốc.
• Centimet khối (cm³): Phù hợp cho các vật thể nhỏ như hộp, lọ.
• Lít (𝑙): Đơn vị phổ biến trong các ngành như thực phẩm và hóa học (1 lít = 1 dm³).

Khối chóp là gì? Các tính chất của khối chóp

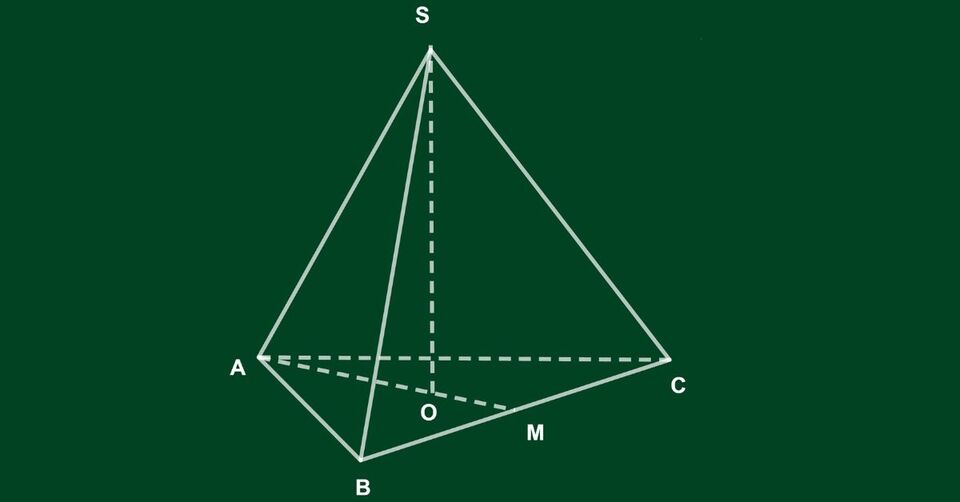
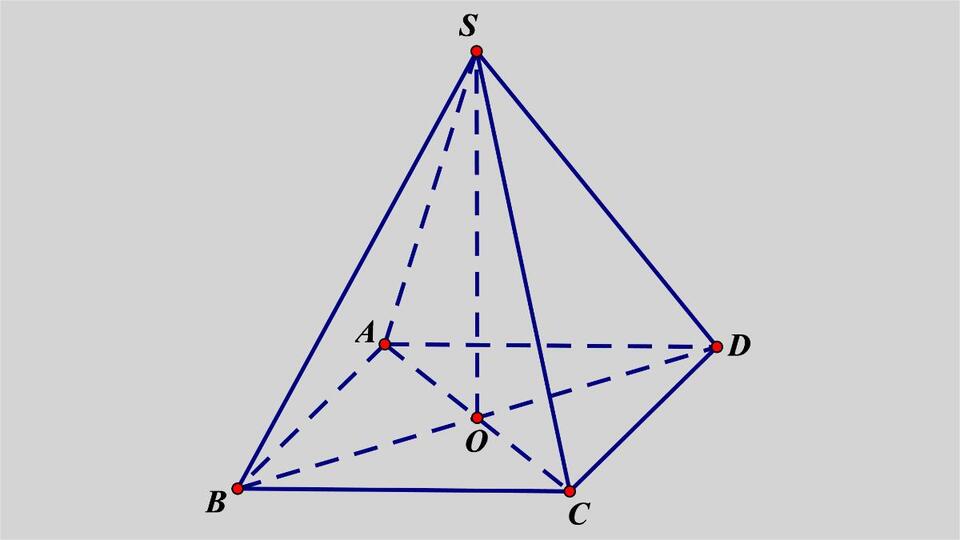
Khối chóp là một loại hình không gian ba chiều với một đáy là một đa giác (tam giác, tứ giác hoặc đa giác n cạnh) và các mặt bên là các tam giác chung đỉnh. Đỉnh chung của các tam giác bên này được gọi là đỉnh chóp.

Khối chóp có những tính chất hình học nổi bật. Những tính chất này giúp chúng ta dễ dàng xác định và tính toán các yếu tố liên quan đến khối chóp trong hình học không gian.

• Khi các cạnh bên có độ dài bằng nhau: Chân đường cao của khối chóp chính là tâm của đường tròn ngoại tiếp đa giác đáy (đường tròn đi qua tất cả các đỉnh của đáy).
• Khi các mặt bên tạo với đáy các góc bằng nhau: Chân đường cao chính là tâm của đường tròn nội tiếp đa giác đáy (đường tròn tiếp xúc với tất cả các cạnh của đáy).
• Khi một mặt bên vuông góc với đáy: Chân đường cao nằm trên giao điểm của đường vuông góc hạ từ đỉnh khối chóp xuống đáy và thuộc mặt bên vuông góc đó.
• Khi hai mặt bên đồng thời vuông góc với mặt đáy: Đường giao tuyến giữa hai mặt bên này sẽ vuông góc với đáy.

Công thức tính thể tích khối chóp

Thể tích của một khối chóp được tính theo công thức:

V=(1/3) * S * h

Trong đó:

• V: Thể tích khối chóp.
• S: Diện tích của đáy (có thể là tam giác, tứ giác hoặc đa giác khác).
• h: Chiều cao từ đỉnh chóp hạ vuông góc xuống mặt phẳng đáy.

Lưu ý:

• Diện tích đáy S phải được tính chính xác, tùy thuộc vào hình dạng của đáy (hình tròn, hình vuông, hình chữ nhật...)
• Chiều cao h phải được đo từ đỉnh của khối chóp đến tâm của đáy.
• Đơn vị của thể tích V sẽ phụ thuộc vào đơn vị của diện tích đáy S và chiều cao h. Ví dụ, nếu S được tính bằng cm² và h được tính bằng cm thì V sẽ được tính bằng cm³.
• Công thức này chỉ áp dụng cho khối chóp có đáy là hình phẳng, không áp dụng cho khối chóp có đáy là hình cong.
• Khi tính thể tích khối chóp, bạn cần kiểm tra xem đã có đủ thông tin cần thiết (diện tích đáy, chiều cao) và áp dụng công thức đúng cách.

Tổng hợp các ví dụ minh họa cách tính thể tích khối chóp

Để hiểu rõ hơn về cách áp dụng công thức tính thể tích khối chóp trong thực tế, chúng ta cùng tìm hiểu qua các ví dụ minh họa dưới đây.

Tính thể tích cho khối chóp có mặt bên vuông góc với mặt đáy

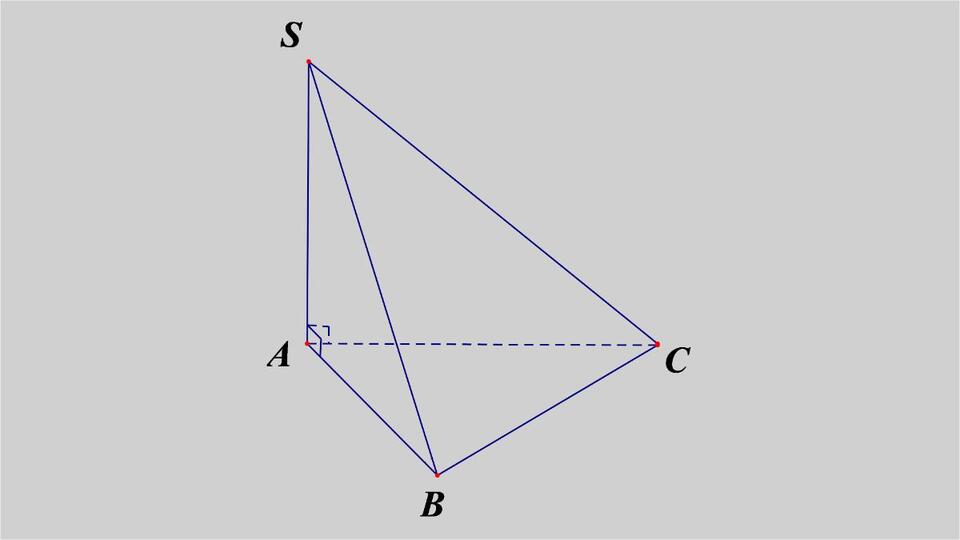
Đề bài: Tính thể tích khối chóp S.ABCD có (SAB) vuông góc với mặt đáy hình chữ nhật ABCD, biết AB = 6 cm, BC = 8 cm và SA = 10 cm.

Lời giải:

• Diện tích đáy: S = AB * BC = 6 * 8 = 48 cm²

Áp dụng công thức tính thể tích khối chóp:

• V=(1/3) * 48 * 10 = 160 cm³

Tính thể tích khối chóp khi cạnh bên vuông góc với mặt đáy

Đề bài: Tìm thể tích khối chóp S.ABC, biết đáy là tam giác ABC vuông tại A và AB = AC = 6 cm, cạnh bên SA = 9 cm và tạo với đáy góc 90 độ.

Lời giải:

• Diện tích đáy: S = (1/2) * AB * AC = (1/2) * 6 * 6 = 18 cm²

Áp dụng công thức tính thể tích khối chóp:

• V = (1/3) * 18 * 9 = 54 cm³

Tính thể tích khối chóp có các cạnh tạo góc vuông từng đôi một

Đề bài: Tính thể tích khối chóp S.ABC có các cạnh bên tạo góc vuông với nhau tại S, biết SA = 5 cm, SB = 3 cm, SC = 4 cm.

Lời giải:

Ta có:

• SA vuông góc với SB
• SA vuông góc với SC

=> SA vuông góc (SBC)

• Chiều cao h = SA = 5 cm
• Diện tích đáy: S = (1/2) * SB * SC = (1/2) * 3 * 4 = 6 cm²
• Thể tích khối chóp: V = (1/3) * 6 * 5 = 10 cm³

Tính thể tích khối chóp khi đáy là hình vuông

Đề bài: Tính thể tích khối chóp S.ABCD có đáy hình vuông cạnh 6 cm, chiều cao h = 10 cm.

Lời giải:

• Diện tích đáy: S = 6 * 6 = 36 cm²
• Áp dụng công thức tính thể tích khối chóp:
• V = (1/3) * 36 * 10 = 120 cm³

Tầm quan trọng của thể tích khối chóp trong học tập và đời sống

Thể tích khối chóp là một khái niệm toán học quan trọng được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và học tập. Dưới đây là một số ví dụ về tầm quan trọng của thể tích khối chóp:

Trong toán học

• Thể tích khối chóp là một phần quan trọng của hình học không gian, giúp chúng ta hiểu về các hình dạng và cấu trúc của các vật thể trong không gian.
• Cách tính thể tích khối chóp được sử dụng để tính toán thể tích của các hình dạng phức tạp, như hình chóp, hình nón, hình trụ...
• Kiến thức về thể tích khối chóp cũng được sử dụng trong các bài toán về tối ưu hóa. Ví dụ như tìm thể tích lớn nhất của một hình chóp với diện tích bề mặt cố định.

Trong kiến trúc và xây dựng

• Công thức tính thể tích khối chóp được sử dụng để tính toán thể tích của các công trình kiến trúc, như nhà cửa, cầu đường.
• Cách tính thể tích khối chóp giúp kiến trúc sư và kỹ sư xây dựng thiết kế và xây dựng các công trình với hình dạng và cấu trúc phức tạp.
• Việc tính thể tích khối chóp cũng được sử dụng để tính toán lượng vật liệu cần thiết cho xây dựng.

Trong vật lý và kỹ thuật

• Ngoài ra, nguyên tắc tính thể tích khối chóp được sử dụng để tính toán thể tích của các vật thể trong không gian. Chẳng hạn như thể tích của một quả bóng, một chiếc xe.
• Nắm bắt kiến thức về thể tích khối chóp giúp chúng ta hiểu về các tính chất vật lý của các vật thể, như trọng lượng, khối lượng.
• Thể tích khối chóp cũng được sử dụng trong các bài toán về động lực học và tĩnh học.

Trong đời sống hằng ngày

• Việc tính toán thể tích khối chóp được sử dụng trong nhiều hoạt động hàng ngày. Điển hình như đo thể tích của các vật dụng, như bình nước, thùng chứa.
• Khi tìm hiểu về thể tích khối chóp sẽ giúp chúng ta hiểu về các khái niệm như tỷ lệ, quy mô.
• Thể tích khối chóp cũng được sử dụng trong các hoạt động thiết kế và tạo mẫu.

Tạm kết

Công thức tính thể tích khối chóp là công cụ mạnh mẽ giúp chúng ta giải quyết nhiều bài toán từ lý thuyết đến thực tiễn. Qua các ví dụ và diễn giải chi tiết trong bài viết, hy vọng bạn đọc đã nắm vững cách áp dụng công thức này một cách hiệu quả. Hãy tiếp tục vận dụng kiến thức này vào thực tế để khám phá thêm nhiều ứng dụng thú vị nhé!

Với sự hỗ trợ của các thiết bị công nghệ hiện đại như laptop, smartphone sẽ giúp bạn học tập hiệu quả hơn. Để tìm mua một mẫu điện thoại thông minh giá tốt, pin bền, cấu hình vừa phải thì bạn hãy đến ngay FPT Shop.

Tham khảo thêm các mẫu điện thoại bán chạy nhất tại đây:

Điện thoại OPPO

Bạn có thể xem thêm:

• Cách sử dụng công thức phép chia trong Excel để xử lý dữ liệu hiệu quả nhất
• Cách kéo thanh công thức nhanh trong Google Sheets, việc thao tác với bảng tính trở nên vô cùng nhanh chóng