Hệ số góc của đường thẳng là gì? Tìm hiểu khái niệm, công thức tính và ứng dụng trong phân tích đồ thị toán học

Bài viết này, FPT Shop sẽ cung cấp cho bạn một cái nhìn toàn diện về hệ số góc, bao gồm khái niệm, công thức tính toán và các ứng dụng thực tế, giúp bạn hiểu rõ hơn về tầm quan trọng của nó trong phân tích toán học.

Khái niệm về hệ số góc

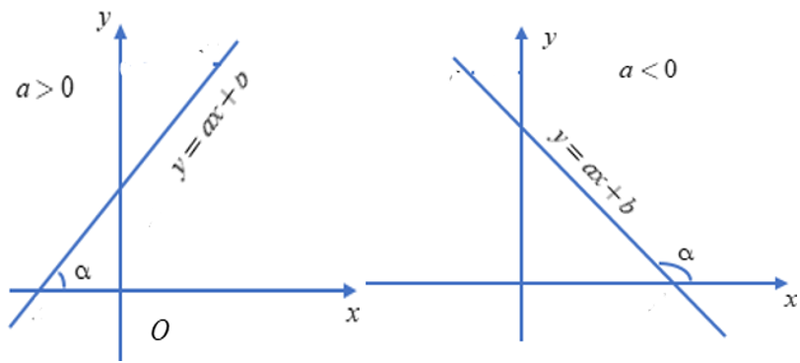
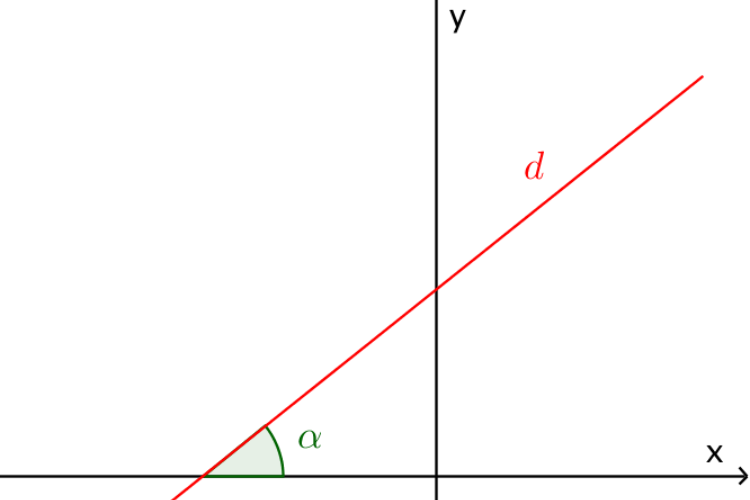
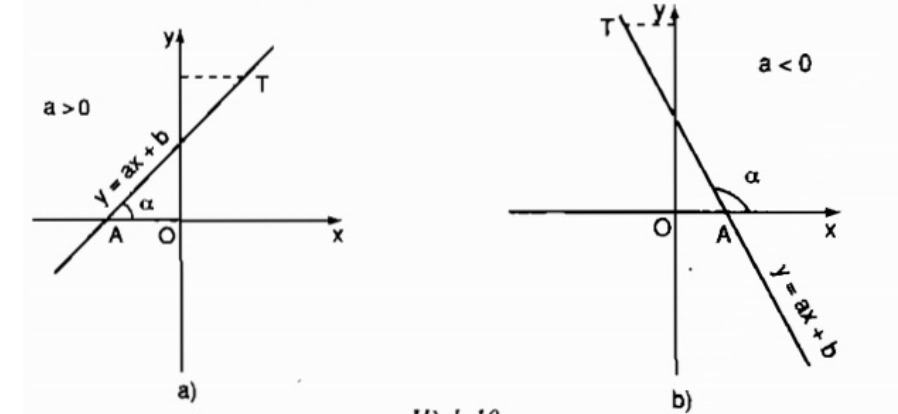
Hệ số góc là một khái niệm quan trọng trong toán học, đặc biệt trong phân tích đồ thị của hàm số bậc nhất. Khi một đường thẳng có phương trình dạng: y = ax + b, a khác 0 thì hệ số góc chính là giá trị của a . Hệ số góc biểu thị độ nghiêng của đường thẳng so với trục hoành (trục Ox).

Nếu a > 0, đường thẳng có xu hướng đi lên khi x tăng. Ngược lại, nếu a<0 , đường thẳng có xu hướng đi xuống. Độ lớn của hệ số góc càng cao thì độ nghiêng của đường thẳng càng lớn.

Hệ số góc còn có ý nghĩa quan trọng trong việc xác định sự biến thiên của hàm số bậc nhất và được sử dụng để đánh giá mức độ thay đổi của giá trị y theo sự thay đổi của x. Điều này có ý nghĩa quan trọng trong các lĩnh vực như kinh tế, vật lý, kỹ thuật và khoa học dữ liệu.

Trong thực tế, hệ số góc còn giúp xác định tốc độ thay đổi của một hàm số so với biến số đầu vào, giúp ích trong việc phân tích xu hướng, dự đoán và tối ưu hóa nhiều quá trình.

Công thức tính hệ số góc

Hệ số góc của đường thẳng được tính bằng công thức:

a = (y₂ – y₁)/(x₂  - x₁)

Hệ số góc có thể được tính trực tiếp từ phương trình đường thẳng hoặc từ hai điểm bất kỳ trên đường thẳng. Đây là một công cụ hữu ích để xác định mối quan hệ giữa hai biến số trong các mô hình toán học và thống kê.

Ứng dụng của hệ số góc

Ứng dụng trong toán học và hình học

Trong toán học, hệ số góc giúp xác định độ dốc của một đường thẳng, từ đó hỗ trợ việc vẽ đồ thị, giải phương trình và chứng minh các tính chất của đường thẳng. Một trong những ứng dụng cơ bản là phân biệt các đường thẳng song song hoặc vuông góc với nhau.

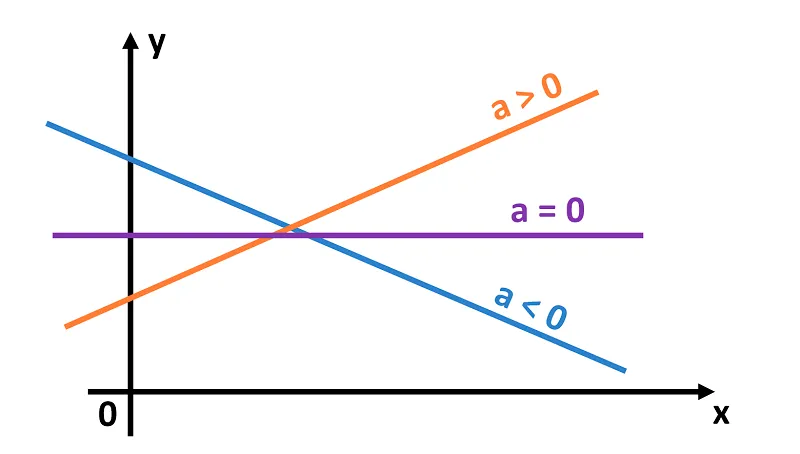
Nếu hai đường thẳng có cùng hệ số góc, chúng sẽ song song, trong khi hai đường có tích hệ số góc bằng một giá trị âm sẽ vuông góc với nhau. Điều này rất quan trọng trong hình học giải tích khi xác định các mối quan hệ giữa những đường trên hệ trục tọa độ.

Ngoài ra, trong các bài toán thực tế về tam giác, hệ số góc giúp xác định độ nghiêng của cạnh tam giác so với một cạnh cố định. Điều này có ích trong việc tính toán khoảng cách, chiều cao hoặc vị trí của các điểm trong không gian.

Ứng dụng trong vật lý và cơ học

Trong vật lý, hệ số góc thường được sử dụng để mô tả sự thay đổi của một đại lượng theo thời gian hoặc theo một yếu tố khác. Ví dụ, trong chuyển động thẳng đều, đồ thị biểu diễn mối quan hệ giữa quãng đường và thời gian có hệ số góc chính là vận tốc của vật thể. Một hệ số góc dương cho thấy vật di chuyển theo hướng tăng dần, trong khi hệ số góc âm thể hiện sự di chuyển ngược lại.

Hệ số góc còn được ứng dụng trong các bài toán về lực và cơ học, chẳng hạn như xác định góc nghiêng của một mặt phẳng và tác động của trọng lực lên một vật thể trên đó. Trong trường hợp xe di chuyển lên hoặc xuống dốc, hệ số góc giúp tính toán lực cần thiết để giữ thăng bằng hoặc để di chuyển trên con dốc đó.

Ngoài ra, trong lĩnh vực điện từ, hệ số góc có thể biểu diễn sự thay đổi của cường độ dòng điện theo thời gian, giúp xác định xu hướng tăng hay giảm của dòng điện trong các mạch điện.

Ứng dụng trong kinh tế và tài chính

Trong kinh tế và tài chính, hệ số góc đóng vai trò quan trọng trong việc phân tích xu hướng dữ liệu, đặc biệt là khi nghiên cứu biến động giá cả, doanh thu hoặc lợi nhuận theo thời gian. Chẳng hạn, trong phân tích chứng khoán, đồ thị thể hiện sự thay đổi của giá cổ phiếu theo thời gian có thể được đánh giá dựa trên hệ số góc. Nếu hệ số góc dương lớn, điều đó có nghĩa là giá cổ phiếu đang tăng nhanh, trong khi hệ số góc âm thể hiện sự sụt giảm của thị trường.

Bên cạnh đó, hệ số góc còn giúp các nhà kinh tế và doanh nghiệp phân tích xu hướng tiêu dùng, từ đó đưa ra các chiến lược Marketing phù hợp. Ví dụ, nếu một công ty nhận thấy xu hướng doanh thu tăng nhanh theo thời gian, họ có thể đầu tư nhiều hơn vào sản xuất và mở rộng thị trường. Ngược lại, nếu xu hướng giảm, cần có biện pháp điều chỉnh để thích nghi với thị trường.

Ứng dụng trong kỹ thuật và xây dựng

Hệ số góc có vai trò quan trọng trong ngành kỹ thuật, đặc biệt là xây dựng và kiến trúc. Nó giúp xác định độ nghiêng của một bề mặt, từ đó hỗ trợ thiết kế cầu đường, mái nhà, bậc thang và nhiều công trình khác. Trong quá trình thi công, các kỹ sư cần tính toán hệ số góc để đảm bảo công trình có độ dốc hợp lý, phù hợp với yêu cầu an toàn và hiệu suất sử dụng.

Một ví dụ điển hình là trong thiết kế đường bộ và đường sắt, việc xác định hệ số góc giúp đảm bảo độ nghiêng của đường phù hợp với điều kiện vận hành của phương tiện. Độ dốc quá lớn có thể khiến phương tiện khó di chuyển, trong khi độ dốc quá nhỏ có thể không đảm bảo khả năng thoát nước hoặc chịu lực tốt.

Ứng dụng trong khoa học dữ liệu và trí tuệ nhân tạo

Trong khoa học dữ liệu, hệ số góc đóng vai trò quan trọng trong phân tích hồi quy tuyến tính, giúp dự đoán xu hướng của dữ liệu dựa trên mối quan hệ giữa hai biến số. Ví dụ, nếu ta muốn dự đoán doanh số bán hàng dựa trên số lượng quảng cáo, hệ số góc giúp xác định mức độ ảnh hưởng của quảng cáo đến doanh số.

Tạm kết

Hệ số góc đóng vai trò quan trọng trong việc xác định độ dốc, hướng và mối quan hệ giữa các biến trong phương trình đường thẳng. Hiểu rõ khái niệm này giúp bạn nắm vững cách phân tích đồ thị, giải quyết bài toán liên quan đến độ nghiêng và xu hướng thay đổi của dữ liệu. Mong rằng những thông tin về hệ số góc trên đây của FPT Shop sẽ hữu ích với bạn.

Để hỗ trợ quá trình học tập và nghiên cứu thì một chiếc laptop phù hợp là điều không thể thiếu. Nếu bạn đang tìm kiếm một mẫu laptop đẹp, giá tốt, chính hãng dành cho học sinh, sinh viên, hãy tham khảo các sản phẩm tại FPT Shop – chúng tôi cung cấp nhiều lựa chọn chất lượng với chế độ bảo hành uy tín cùng các ưu đãi hấp dẫn!

Xem thêm về các sản phẩm laptop ASUS nhiều ưu đãi tại đây:

• Laptop ASUS

Xem thêm:

• 1 độ bằng bao nhiêu phút? Bật mí bí quyết chuyển đổi đơn vị đo nhanh và dễ dàng nhất
• Bật mí cách dùng lệnh đo góc trong CAD cực kỳ đơn giản