Hàm SQRT trong Excel: Công cụ mạnh mẽ để tính toán căn bậc hai trong bảng tính

Trong Excel, hàm SQRT là một trong những công cụ hữu ích mà người dùng không thể bỏ qua khi làm việc với các phép toán căn bậc hai. Dù bạn là người mới bắt đầu sử dụng Excel hay đã là một chuyên gia trong lĩnh vực xử lý dữ liệu, việc hiểu rõ và khai thác tối đa sức mạnh của hàm SQRT sẽ giúp bạn tiết kiệm thời gian và nâng cao hiệu quả công việc. 

Trong bài viết này, chúng ta sẽ cùng tìm hiểu về cách sử dụng hàm SQRT để giúp bạn có thể tối ưu hóa việc tính toán căn bậc hai trong bảng tính nhé.

Định nghĩa hàm SQRT trong Toán học

Hàm căn bậc hai (SQRT) là một trong những phép toán cơ bản trong toán học dùng để tìm ra một số thực không âm mà khi bình phương nó sẽ bằng với số cho trước. Ví dụ, căn bậc hai của 25 là 5, vì 5² = 25. Do vậy, hàm căn bậc hai rất quan trọng trong nhiều lĩnh vực toán học và ứng dụng thực tiễn như giải phương trình, tính toán diện tích, phân tích dữ liệu khoa học và trong cả các bài toán liên quan đến vật lý hay kỹ thuật​.

Ứng dụng của hàm SQRT trong thực tế

Hàm căn bậc hai (SQRT) là một trong những khái niệm toán học cơ bản và ứng dụng của nó rất rộng rãi trong cuộc sống hàng ngày. Dưới đây là một số ứng dụng phổ biến của hàm SQRT trong thực tế:

• Ứng dụng trong xây dựng và kiến trúc: Trong ngành xây dựng và thiết kế kiến trúc, hàm SQRT được sử dụng để tính toán khoảng cách và chiều dài của các cạnh trong các hình học vuông góc. Cụ thể: Trong việc áp dụng định lý Pythagoras, người ta sử dụng căn bậc hai để xác định chiều dài của cạnh huyền trong tam giác vuông khi biết chiều dài của hai cạnh góc vuông. Điều này rất quan trọng khi thiết kế các cấu trúc công trình, giúp đảm bảo tính chính xác trong các phép đo và xây dựng.
• Ứng dụng trong tài chính: Trong lĩnh vực tài chính, hàm SQRT được sử dụng để tính toán các chỉ số tài chính như tỷ lệ lợi nhuận, đặc biệt là trong các công thức liên quan đến giá trị hiện tại và giá trị tương lai của các khoản đầu tư. Công thức này giúp các nhà đầu tư tính toán được hiệu quả của một khoản đầu tư trong suốt thời gian nhất định.
• Ứng dụng trong vật lý: Trong vật lý, hàm SQRT được sử dụng để tính toán nhiều yếu tố quan trọng như tốc độ trong chuyển động thẳng đều, năng lượng trong các hệ thống vật lý và khoảng cách trong các hệ điều hành cơ học. Một ví dụ điển hình là việc tính toán khoảng cách giữa các điểm trong không gian hai chiều hoặc ba chiều. Đó là một công thức cơ bản mà nhiều nhà vật lý sử dụng trong nghiên cứu.
• Ứng dụng trong khoa học máy tính và đồ họa: Trong lĩnh vực khoa học máy tính, hàm SQRT rất hữu ích khi cần tính toán khoảng cách giữa các điểm trong không gian hai chiều hoặc ba chiều, đặc biệt trong các trò chơi điện tử và đồ họa máy tính. Điều này giúp xác định vị trí các đối tượng, từ đó tạo ra các hiệu ứng hình ảnh và chuyển động mượt mà.
• Ứng dụng trong y học: Căn bậc hai cũng được ứng dụng trong các phép đo y tế. Ví dụ: Trong tính toán các chỉ số sức khỏe như BMI (chỉ số khối cơ thể), việc sử dụng căn bậc hai giúp xác định mức độ béo phì của một người dựa trên chiều cao và cân nặng.

Như vậy, hàm SQRT là một khái niệm lý thuyết trong toán học và là một công cụ mạnh mẽ, ứng dụng trong nhiều lĩnh vực khác nhau của cuộc sống.

Chức năng của hàm SQRT trong Excel

Hàm SQRT trong Excel là một công cụ mạnh mẽ được sử dụng để tính căn bậc hai của một số. Chức năng này sẽ giúp người dùng dễ dàng thực hiện các phép toán về căn bậc hai ngay trong bảng tính mà không cần phải làm tính thủ công. Đặc biệt, hàm này chỉ nhận giá trị không âm, tức là các số dương hoặc bằng 0 và trả về kết quả là căn bậc hai của số đó. Vì vậy, hàm SQRT cực kỳ hữu ích trong các phép toán toán học phức tạp, đặc biệt là khi làm việc với các số liệu lớn hoặc trong các bài toán yêu cầu tính toán chuẩn xác nhanh chóng.

Cách sử dụng hàm SQRT trong Excel

Trong Excel, hàm SQRT là một công cụ cực kỳ hữu ích giúp bạn tính toán căn bậc hai của các số một cách nhanh chóng và chính xác. Dưới đây, chúng ta sẽ đi qua cú pháp cơ bản của hàm SQRT, khả năng kết hợp với các hàm khác và thực hành qua một số ví dụ thực tế.

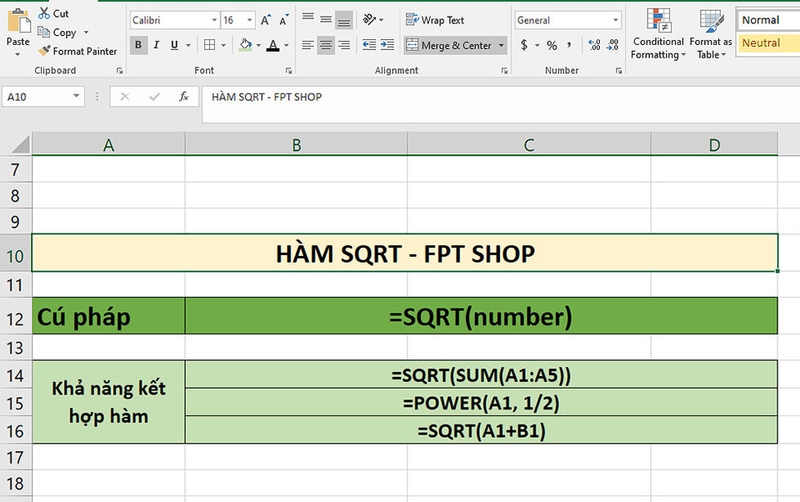
1. Cú pháp cơ bản

Cú pháp của hàm SQRT trong Excel rất đơn giản:

• =SQRT(number)

Trong đó:

• number là số mà bạn muốn tính căn bậc hai. Bạn cần lưu ý rằng số này phải là một giá trị không âm (số dương hoặc 0). Nếu bạn nhập số âm, Excel sẽ báo lỗi #NUM!.

2. Khả năng kết hợp hàm

Hàm SQRT có thể được kết hợp với nhiều hàm khác trong Excel để giải quyết các bài toán phức tạp hơn. Một số ví dụ về việc kết hợp hàm SQRT với các hàm khác:

• Kết hợp với hàm SUM: Bạn có thể tính căn bậc hai của tổng các giá trị với cú pháp là =SQRT(SUM(A1:A5)).
• Kết hợp với hàm POWER: Bạn cũng có thể tính căn bậc hai bằng cách sử dụng hàm POWER với cú pháp là =POWER(A1, 1/2).
• Kết hợp với các phép toán khác: Bạn còn có thể tính toán căn bậc hai sau khi thực hiện các phép toán khác như cộng hoặc trừ.

3. Ví dụ thực tế

Bây giờ, bạn hãy cùng FPT Shop thực hành với bảng tính có dữ liệu như bên dưới. Bạn có thể tạo bảng tính tương tự vào Excel và thử áp dụng các công thức sau.

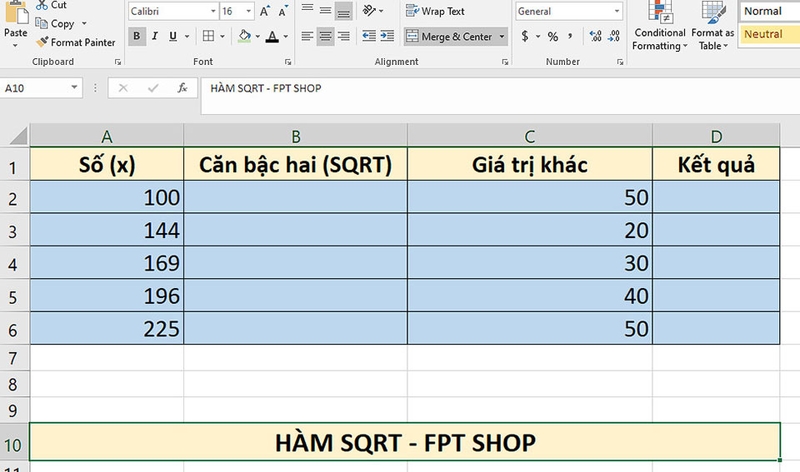
Ví dụ 1: Tính căn bậc hai của các số trong bảng và cộng thêm giá trị khác

Mục tiêu: Tính căn bậc hai của các số trong cột "Số (x)", sau đó cộng thêm giá trị trong cột "Giá trị khác". Các bước thực hiện như sau:

Bước 1: Tại ô B2, bạn hãy nhập công thức tính căn bậc hai của số trong ô A2 với cú pháp:

• =SQRT(A2)

Sau khi nhập công thức, bạn sẽ thấy kết quả là 10 trong ô B2 (vì căn bậc hai của 100 là 10). Bạn có thể sao chép công thức cho những cột bên dưới của ô B2.

Bước 2: Tại ô D2, bạn nhập công thức để cộng thêm giá trị từ cột "Giá trị khác" vào kết quả căn bậc hai:

• =B2+C2

Kết quả sẽ là 60 (10 + 50). Sau đó, bạn có thể kéo công thức ở ô D2 xuống các ô còn lại để tính toán cho các giá trị khác trong bảng.

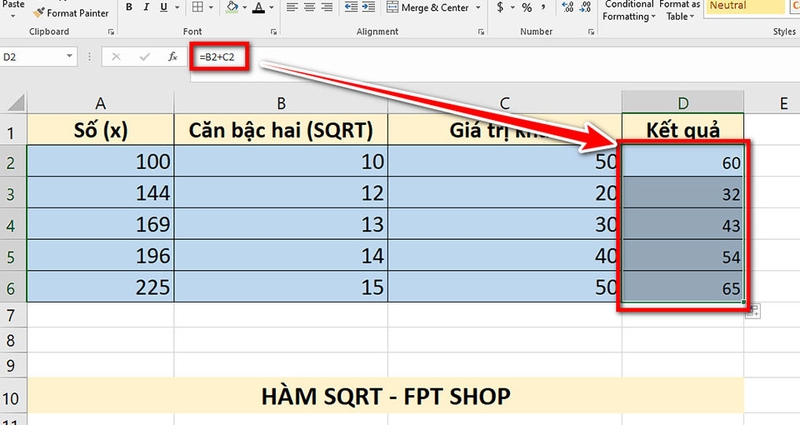
Ví dụ 2: Tính căn bậc hai của tổng các giá trị trong cột "Số (x)" và trừ đi một giá trị khác

Mục tiêu: Tính căn bậc hai của tổng các giá trị trong cột "Số (x)" và sau đó trừ đi giá trị trong cột "Giá trị khác". Các bước thực hiện như sau:

Bước 1: Ở ô D2, bạn hãy nhập công thức tính tổng các giá trị trong cột "Số (x)" và tính căn bậc hai của tổng:

• =SQRT(SUM(A2:A6))

Kết quả sẽ là 28.87905816 (tổng các số là 834 và căn bậc hai của 834 là 28.87905816).

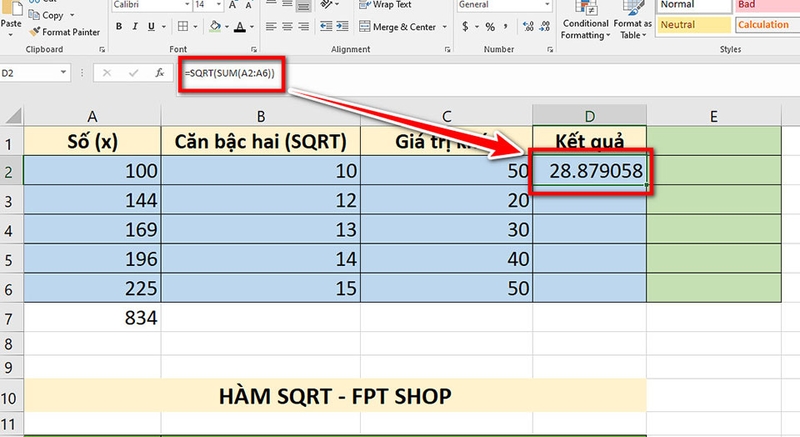
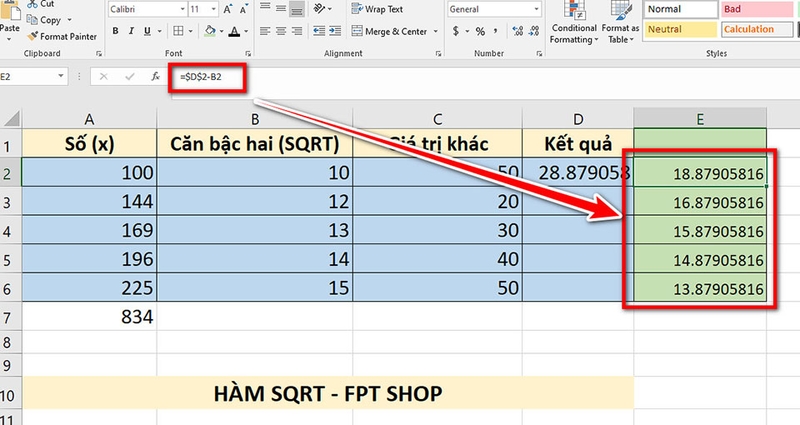
Bước 2: Ở ô E2, bạn hãy nhập công thức để trừ đi giá trị trong ô B2 từ kết quả ở ô D2 (bạn hãy nhấn F4 ở ô D2 để cố định ô trong công thức tính):

• =$D$2-B2

Sau đó, bạn hãy kéo công thức từ ô E2 xuống các ô còn lại trong cột E để tính toán cho các số còn lại.

Tạm kết

Như vậy, hàm SQRT trong Excel là một phần không thể thiếu trong việc xử lý và phân tích dữ liệu. Việc nắm vững cách sử dụng hàm SQRT sẽ giúp bạn dễ dàng tính toán căn bậc hai, đồng thời áp dụng nó vào nhiều tình huống khác nhau trong công việc hàng ngày. Qua bài viết này, FPT Shop hy vọng bạn đã có được những kiến thức bổ ích để sử dụng Excel một cách hiệu quả hơn.

Nếu bạn có nhu cầu mua laptop văn phòng chính hãng để làm việc linh hoạt hơn, hãy dành thời gian đến với các cửa hàng của FPT Shop hoặc truy cập vào đường link bên dưới nhé.

• Laptop văn phòng

Xem thêm:

• Tìm hiểu hàm XOR trong Excel: Công thức và ứng dụng thực tế trong phân tích dữ liệu
• Giải mã hàm GAMMA trong Excel: Công thức, cách dùng và các ứng dụng thực tiễn
• Hướng dẫn cách sử dụng hàm lọc trùng trong Excel chi tiết từ A-Z