Cách tính chu vi hình thang dễ nhớ, kèm bài tập luyện tập từ cơ bản đến nâng cao

Trong hình thang, có nhiều đơn vị và đại lượng liên quan đến việc tính toán các yếu tố như chu vi, diện tích và các chiều dài khác. Cách tính chu vi hình thang là một bài toán cơ bản trong hình học, yêu cầu bạn phải hiểu rõ cấu trúc của hình thang và các đặc điểm của từng loại hình thang như hình thang vuông, hình thang cân, hay hình thang thường để áp dụng công thức chính xác.

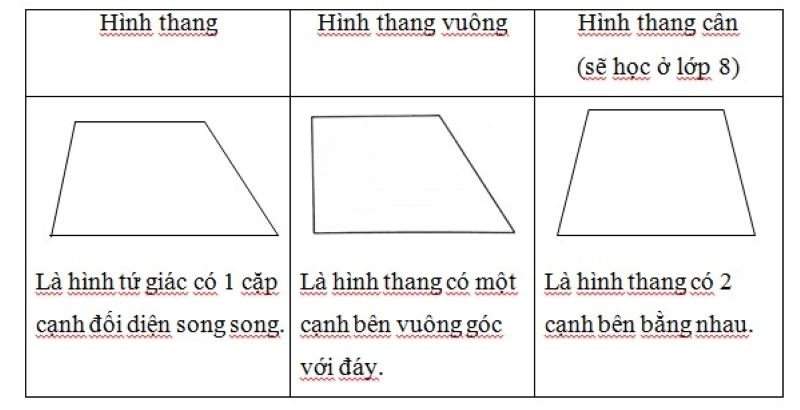
Định nghĩa hình thang

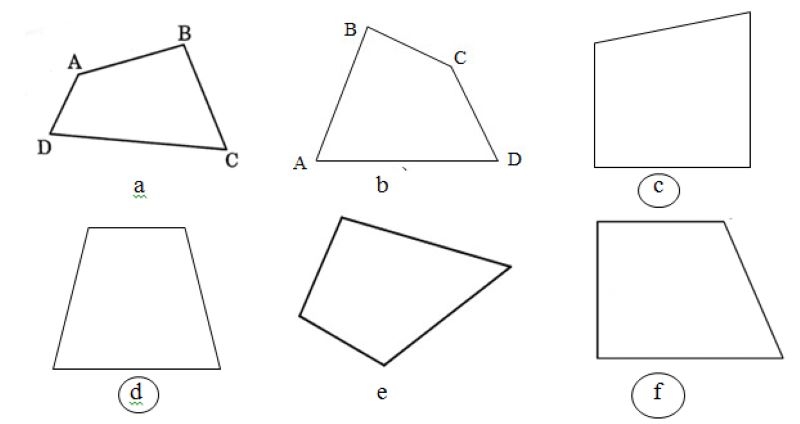
Hình thang là một tứ giác có hai cạnh đối song song và hai cạnh còn lại không song song. Hai cạnh song song này được gọi là cạnh đáy và hai cạnh không song song được gọi là cạnh bên.

Tính chu vi hình thang thường

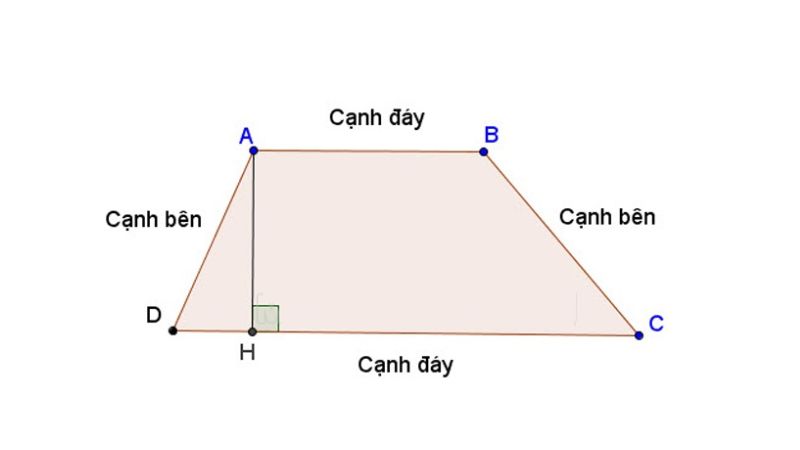
Để thực hiện cách tính chu vi hình thang, bạn chỉ cần cộng tổng độ dài của tất cả bốn cạnh lại với nhau.

• Công thức tính chu vi hình thang như sau: P=a+b+c+d

Trong đó:

• P là chu vi của hình thang.
• a và b là hai cạnh đáy.
• c và d là hai cạnh bên.

Ví dụ: Nếu hình thang có các cạnh đáy lần lượt là 6 cm và 10 cm, hai cạnh bên là 4 cm và 5 cm, thì cách tính chu vi hình thang như sau: P=6+10+4+5=25 cm.

Tính chu vi một số hình thang đặc biệt

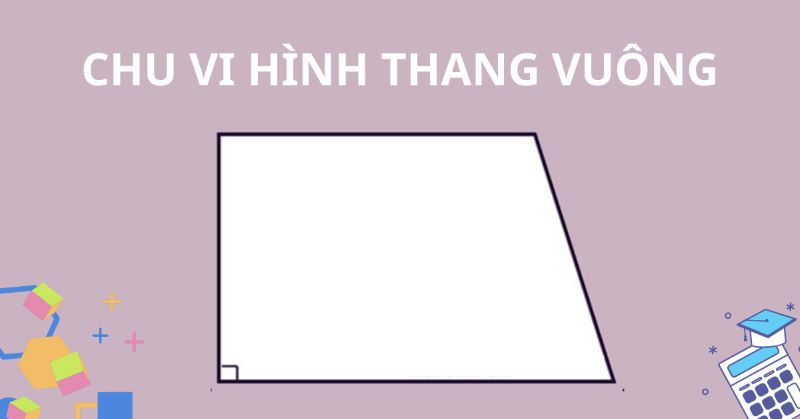
Chu vi hình thang vuông

Hình thang vuông là hình thang có một góc vuông, tức là một trong hai cạnh bên vuông góc với đáy. Cách tính chu vi hình thang vuông vẫn giống với hình thang thông thường:

• P=a+b+c+d

Trong đó:

• a và b là hai cạnh đáy.
• c là cạnh bên vuông góc với đáy.
• d là cạnh bên còn lại (có thể là cạnh xiên).

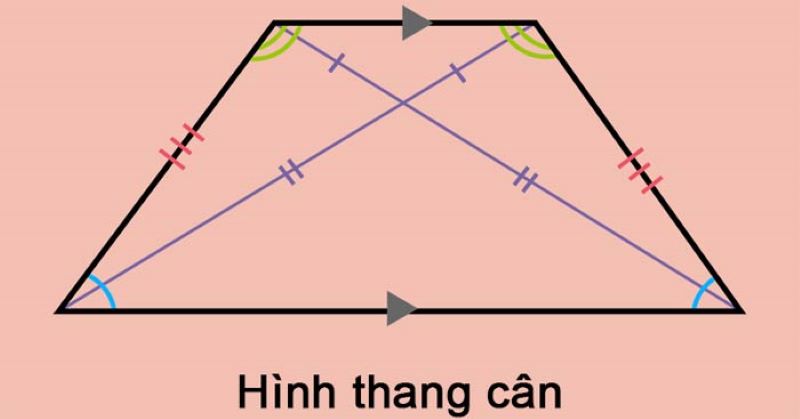
Chu vi hình thang cân

Hình thang cân là hình thang có hai cạnh bên bằng nhau. Cách tính chu vi hình thang cân cũng giống công thức tổng quát cho hình thang: P=a+b+2c.

Trong đó:

• a và b là hai cạnh đáy.
• c là độ dài của hai cạnh bên (vì chúng bằng nhau).

Đề bài: Cho một hình thang cân có hai cạnh đáy lần lượt là a=8 cm và b=14 cm và độ dài hai cạnh bên đều bằng c=5 cm. Tính chu vi hình thang.

Giải:

Sử dụng công thức chu vi hình thang cân: P=a+b+2c

Thay các giá trị vào: P = 8+14+2×5 = 32 cm.

Chu vi hình thang vuông cân

Hình thang vuông cân là một trường hợp đặc biệt, trong đó một cạnh bên vuông góc với đáy và hai cạnh bên bằng nhau (tức cạnh vuông góc và cạnh xiên có cùng chiều dài). Công thức tính chu vi trong trường hợp này là:

• P=a+b+2c

Trong đó:

• a và b là hai cạnh đáy.
• c là độ dài của hai cạnh bên (bằng nhau).

Đề bài: Cho một hình thang vuông cân có hai cạnh đáy lần lượt là a=7 cm và b=12 cm, độ dài hai cạnh bên (cạnh vuông góc và cạnh xiên) đều bằng c=6 cm. Tính chu vi hình thang.

Giải:

Sử dụng công thức chu vi hình thang vuông cân: P=a+b+2c

Thay các giá trị vào: P = 7+12+2×6 = 31 cm

Tóm lại, công thức tính chu vi cho từng loại hình thang chỉ khác nhau khi hình thang có đặc điểm cân hoặc vuông.

Một số bài tập luyện tập tính chu vi hình thang dạng khó

Bài tập 1. Cho một hình thang vuông có:

• Đáy lớn b=24 cm
• Đáy nhỏ a=16 cm
• Cạnh vuông góc với đáy c=10 cm
• Góc giữa cạnh bên và đáy lớn là 30 độ

Tính chu vi của hình thang vuông này.

Bài tập 2. Cho một hình thang vuông có:

• Đáy lớn b=20 cm
• Đáy nhỏ a=12 cm
• Đường cao h=9 cm

Biết rằng một trong hai cạnh bên vuông góc với đáy, hãy tính chu vi của hình thang vuông này.

Bài tập 3. Cho một hình thang cân có:

• Đáy lớn b=16 cm
• Đáy nhỏ a=10 cm
• Đường cao h=8 cm

Tính chu vi của hình thang cân này.

Bài tập 4. Cho một hình thang cân có:

• Đáy lớn b=26 cm
• Đáy nhỏ a=14 cm
• Đường cao h=12 cm
• Góc giữa cạnh bên và đáy lớn là 60 độ.

Tính chu vi của hình thang cân.

Tạm kết

Như vậy, FPT Shop đã chia sẻ xong cách tính chu vi hình thang, trong một số trường hợp đặc biệt, bạn cần vận dụng thêm các kiến thức về định lý Pythagore và công thức lượng giác để tìm các cạnh chưa biết. Bằng cách nắm vững các phương pháp và kỹ năng tính toán này, bạn có thể giải quyết các bài toán liên quan đến chu vi hình thang một cách chính xác và hiệu quả.

Bạn đang tìm kiếm một chiếc laptop gọn nhẹ để phục vụ cho công việc học tập, làm những bài tập thuyết trình, đừng bỏ lỡ những mẫu laptop cấu hình mạnh, giá ưu đãi tại FPT Shop.

Tham khảo chi tiết sản phẩm tại:

• Laptop sinh viên

Xem thêm:

• Chia sẻ cách tính chiều dài hình chữ nhật cực dễ hiểu, chính xác và nhanh chóng
• Tất tần tật về diện tích tam giác vuông và các công thức quan trọng không thể quên