Hình bình hành có tâm đối xứng không? Giải thích dễ hiểu, cách xác định và ứng dụng thực tế

Hình bình hành có tâm đối xứng không? Đây là một câu hỏi vừa thú vị vừa quan trọng trong hình học, bởi tâm đối xứng không chỉ là kiến thức lý thuyết mà còn liên quan trực tiếp đến cách tính toán, thiết kế và suy luận hình học. Khi hiểu được tâm đối xứng của một hình, bạn sẽ dễ dàng nhìn ra mối quan hệ giữa các điểm, các cạnh, các đường chéo, từ đó giải nhanh nhiều dạng bài khác nhau.

Trong thực tế, tính đối xứng được ứng dụng rộng rãi trong kiến trúc, công nghiệp, thiết kế sản phẩm và cả trong cách xây dựng hình ảnh trực quan cho giáo dục. Tuy nhiên, không ít bạn học sinh hay nhầm lẫn giữa tâm đối xứng và trục đối xứng, hoặc cho rằng chỉ những hình “đều” mới có tâm đối xứng. Vậy rốt cuộc tâm đối xứng là gì và hình bình hành có tâm đối xứng không? Mời bạn cùng theo dõi bài viết dưới đây để hiểu rõ, nhớ lâu và áp dụng đúng.

Tâm đối xứng là gì?

Tâm đối xứng là một điểm đặc biệt của hình phẳng. Khi bạn quay hình quanh điểm đó một góc 180 độ, hình mới thu được sẽ trùng khớp với hình ban đầu. Nói cách khác, tâm đối xứng là điểm trung tâm giúp hình giữ nguyên hình dạng sau phép quay nửa vòng.

Khái niệm này rất quan trọng vì nó giúp chúng ta mô tả tính “cân đối” của hình, đồng thời là chìa khóa để chứng minh các điểm đối xứng và các đoạn thẳng bằng nhau trong nhiều bài toán.

Tùy theo đối tượng và không gian nghiên cứu, đối xứng có thể được xét qua điểm, qua đường thẳng hoặc qua mặt phẳng. Nhưng trong chương trình hình học phẳng phổ thông, khi nhắc đến tâm đối xứng, ta hiểu đó là một điểm, quanh đó hình có thể quay 180 độ để trùng khít với chính nó.

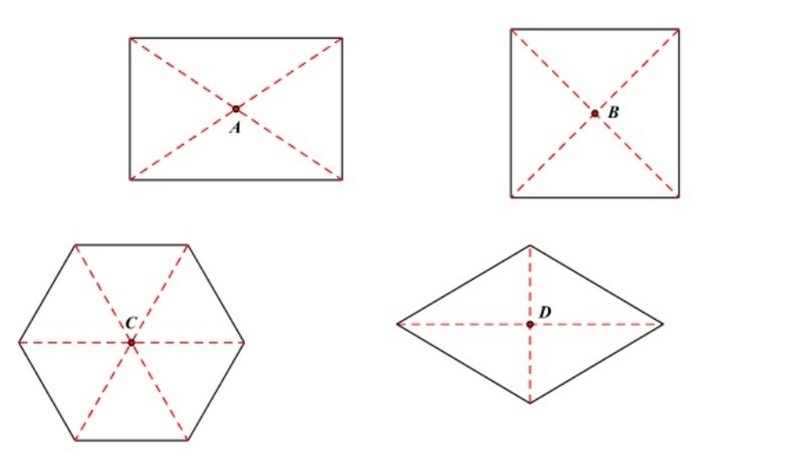
Ví dụ về tâm đối xứng trong các hình quen thuộc

• Hình tròn: Tâm đối xứng chính là tâm của hình tròn. Dù quay hình tròn quanh tâm bao nhiêu lần, hình vẫn giữ nguyên.
• Hình vuông: Tâm đối xứng là giao điểm của 2 đường chéo. Khi quay 180 độ quanh điểm này, hình vuông vẫn trùng khít.
• Hình chữ nhật: Tâm đối xứng cũng là giao điểm của 2 đường chéo.
• Hình thoi: Tâm đối xứng là giao điểm 2 đường chéo.
• Hình bình hành: Tâm đối xứng cũng nằm tại giao điểm 2 đường chéo, đây là điểm quan trọng nhất bạn cần ghi nhớ.

Không phải hình nào cũng có tâm đối xứng. Ví dụ:

• Tam giác đều không có tâm đối xứng theo nghĩa quay 180 độ trùng khít.
• Hình thang cân cũng không có tâm đối xứng, dù có thể có trục đối xứng.

Điều này giúp bạn thấy rõ rằng tâm đối xứng và trục đối xứng là 2 khái niệm khác nhau. Có hình có trục đối xứng nhưng không có tâm đối xứng, và ngược lại.

Hình bình hành có tâm đối xứng không?

Đến đây, chúng ta quay lại câu hỏi trọng tâm. Hình bình hành có tâm đối xứng không? Câu trả lời là có. Với mọi hình bình hành, tâm đối xứng luôn tồn tại và chính là giao điểm của 2 đường chéo.

Bạn có thể hiểu điều này theo cách trực quan. Trong hình bình hành, 2 đường chéo luôn cắt nhau tại trung điểm của mỗi đường. Điều đó nghĩa là giao điểm đường chéo chia mỗi đường chéo thành 2 đoạn bằng nhau. Khi bạn quay hình 180 độ quanh điểm giao này, mỗi đỉnh sẽ “đổi chỗ” với đỉnh đối diện và hình giữ nguyên cấu trúc.

Nói gọn lại: Hình bình hành luôn có tâm đối xứng và nó là giao điểm của 2 đường chéo. Tính chất này đúng cho cả hình bình hành thường, hình chữ nhật và hình thoi vì chúng đều là các trường hợp đặc biệt của hình bình hành.

Nếu bạn đang học phần này, bạn cũng có thể đọc thêm bài liên quan để hiểu sâu hơn về định nghĩa, tính chất và công thức của hình bình hành, từ đó làm bài tập nhanh hơn.

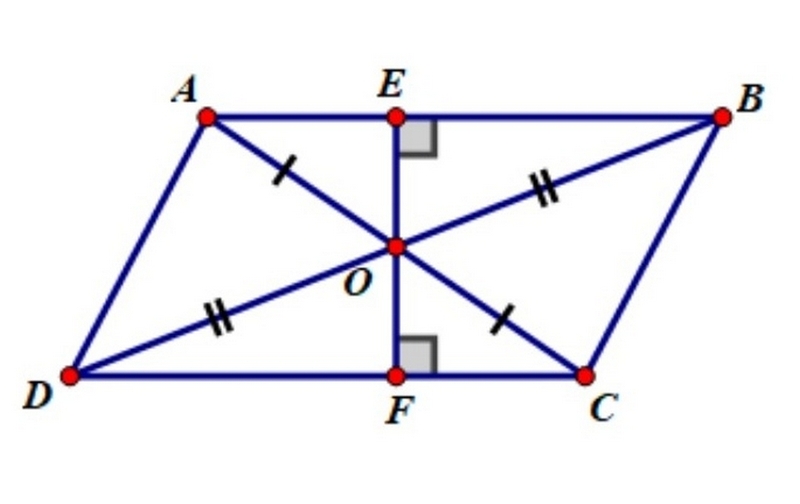
Tâm đối xứng của hình bình hành là gì?

Tâm đối xứng của hình bình hành là giao điểm của 2 đường chéo. Đây là kết luận quan trọng và có thể chứng minh dựa trên tính chất đường chéo của hình bình hành.

Vì sao giao điểm 2 đường chéo lại là tâm đối xứng?

Trong hình bình hành, 2 đường chéo có một tính chất cực kỳ nổi bật:
Chúng cắt nhau tại trung điểm của mỗi đường.

Điều này có nghĩa là nếu gọi O là giao điểm của đường chéo AC và BD, thì:

• OA = OC
• OB = OD

Khi quay hình quanh điểm O một góc 180 độ:

• Điểm A sẽ chuyển đến vị trí của điểm C
• Điểm B sẽ chuyển đến vị trí của điểm D

Vì vậy, toàn bộ hình bình hành trùng khít với chính nó.

So sánh với hình chữ nhật và hình thoi

Hình chữ nhật và hình thoi đều là hình bình hành đặc biệt, nên chúng cũng có tâm đối xứng ở giao điểm 2 đường chéo.

• Với hình chữ nhật, điểm giao đường chéo còn là tâm của hình, giúp bạn dễ xác định khoảng cách đến các đỉnh.
• Với hình thoi, giao điểm 2 đường chéo còn có thêm tính chất đường chéo vuông góc và phân giác góc, nên rất hay được dùng trong chứng minh.

Những nhầm lẫn về câu hỏi hình bình hành có tâm đối xứng không

Nhiều bạn hay hiểu sai rằng chỉ khi các cạnh bằng nhau hoặc góc vuông thì hình mới có tâm đối xứng. Thực tế, điều đó không đúng. Vậy vì sao có sự nhầm lẫn? Thường là do nhiều bạn lẫn giữa:

• Tâm đối xứng là quay 180 độ trùng khít.
• Trục đối xứng là gấp đôi qua một đường thẳng.

Hình bình hành thường không có trục đối xứng, nhưng vẫn có tâm đối xứng. Còn hình chữ nhật và hình thoi có thể vừa có tâm đối xứng vừa có trục đối xứng, nên dễ khiến người học nghĩ rằng phải “đều” mới có tâm đối xứng.

Tâm đối xứng của hình bình hành nằm ở đâu? Cách xác định nhanh

Trong bài tập, bạn thường gặp yêu cầu xác định tâm đối xứng, chứng minh 2 điểm đối xứng hoặc suy ra các đoạn bằng nhau. Bạn có thể làm theo 2 cách phổ biến dưới đây.

• Cách 1 - Dựa vào đường chéo: Bạn vẽ hoặc xác định 2 đường chéo của hình bình hành. Điểm giao nhau của chúng chính là tâm đối xứng.
• Cách 2 - Dựa vào trung điểm của 2 đoạn nối đỉnh đối diện: Vì tâm đối xứng là trung điểm của mỗi đường chéo, bạn có thể tìm trung điểm của AC hoặc BD. Khi tìm được trung điểm của 1 đường chéo thì đó chính là tâm đối xứng, vì trung điểm của AC cũng đồng thời là trung điểm của BD.

Ứng dụng tâm đối xứng của hình bình hành trong thực tế

Tâm đối xứng không chỉ là kiến thức để làm bài tập. Khi hiểu rõ tâm đối xứng của hình bình hành, bạn sẽ thấy khái niệm này xuất hiện rất nhiều trong đời sống và các ngành kỹ thuật.

Tính toán hình học

Khi biết tâm đối xứng, bạn có thể suy ra nhanh nhiều yếu tố của hình bình hành như:

• Quan hệ bằng nhau giữa các đoạn
• Các điểm đối xứng qua tâm
• Nhiều phép biến đổi hình học như quay 180 độ

Đặc biệt, tâm đối xứng giúp bạn rút gọn chứng minh, vì bạn có thể thay vì chứng minh từng đoạn, hãy dùng phép đối xứng qua tâm để suy ra các phần tương ứng.

Thiết kế và kiến trúc

Trong thiết kế, việc tạo ra các cấu trúc cân đối giúp công trình hài hòa và ổn định hơn. Nhiều chi tiết trong kiến trúc sử dụng mô típ hình bình hành như các mảng tường, ô trang trí, lan can, mái che, cửa sổ dạng nghiêng. Khi xác định đúng tâm đối xứng, người thiết kế dễ bố trí các phần tương ứng sao cho cân bằng về mặt thị giác.

Công nghiệp và cơ khí

Trong công nghiệp, tâm đối xứng giúp thiết kế những bộ phận hoạt động ổn định, hạn chế rung lắc. Những chi tiết dạng khung hoặc tấm ghép hình bình hành có thể được tính toán để tạo sự cân bằng lực. Việc xác định tâm đối xứng còn hỗ trợ trong quá trình gia công, đo đạc và kiểm tra độ chính xác của sản phẩm.

Giáo dục và trực quan hóa kiến thức

Trong giáo dục, tâm đối xứng giúp học sinh hiểu rõ hơn về biến đổi hình học. Khi dạy đối xứng, giáo viên thường dùng hình bình hành để minh họa cho phép quay 180 độ, cách xác định điểm tương ứng và các tính chất liên quan đến đường chéo.

Ngoài ra, việc luyện tập với các hình có tâm đối xứng còn giúp bạn phát triển tư duy không gian, một kỹ năng quan trọng khi học hình học và cả khi áp dụng vào các ngành kỹ thuật, thiết kế.

Hình bình hành có mấy tâm đối xứng?

Đây là câu hỏi rất hay xuất hiện trong phần nâng cao. Với hình bình hành, câu trả lời là: Hình bình hành chỉ có 1 tâm đối xứng, đó là giao điểm 2 đường chéo.

Vì sao chỉ có 1? Vì tâm đối xứng phải là điểm mà khi quay 180 độ, toàn bộ hình trùng khít. Trong hình bình hành, chỉ có giao điểm 2 đường chéo thỏa điều kiện này.

Xác định tâm đối xứng hình bình hành được áp dụng trong thực tiễn

Trong thực tế, việc xác định tâm đối xứng của hình bình hành giúp ích trong nhiều hoạt động:

• Trong bản vẽ kỹ thuật, tâm đối xứng giúp bố trí chi tiết nhanh hơn, nhất là các phần cần đối xứng để cân bằng.
• Trong thiết kế đồ họa, tâm đối xứng giúp tạo pattern và bố cục hài hòa.
• Trong mô hình học tập, tâm đối xứng hỗ trợ học sinh thao tác, quay hình và kiểm chứng tính chất.

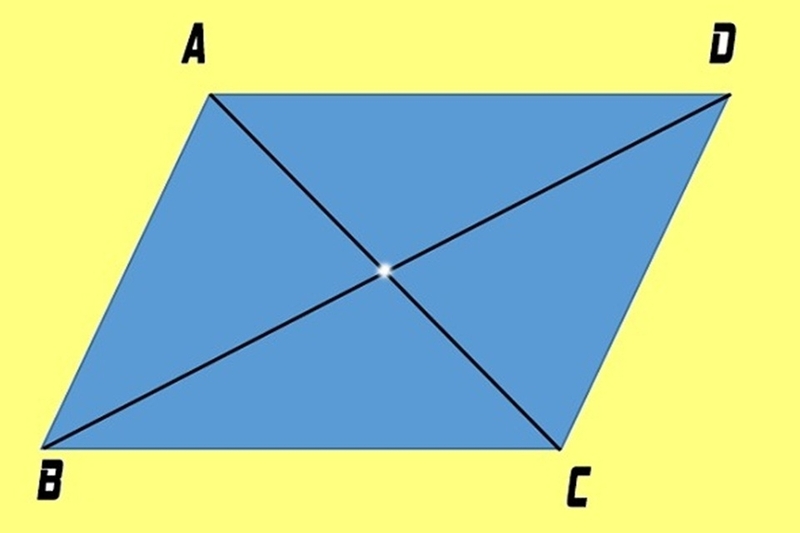
Đặc biệt, khi bạn học tốt phần này, bạn sẽ thấy các bài liên quan đến rút gọn chứng minh, tìm đoạn thẳng bằng nhau, hoặc chứng minh trung điểm trở nên nhẹ nhàng hơn rất nhiều.

Kết luận

Trên đây là giải đáp đầy đủ cho câu hỏi hình bình hành có tâm đối xứng không. Hy vọng qua phần giải thích về khái niệm tâm đối xứng, cách xác định giao điểm 2 đường chéo và các ứng dụng thực tế, bạn đã hiểu rõ hơn về tính chất đặc trưng của hình bình hành. Khi nắm vững nội dung này, bạn sẽ thấy các bài hình học liên quan đến đối xứng và đường chéo trở nên dễ thở hơn rất nhiều. 

Muốn học hình học dễ hơn và luyện bài đều đặn, một chiếc laptop hoặc máy tính bảng ổn định sẽ giúp bạn tra cứu, vẽ hình và làm bài nhanh hơn mỗi ngày. Tại FPT Shop, bạn có thể chọn nhiều thiết bị phục vụ học tập với mức giá dễ tiếp cận, kèm ưu đãi và bảo hành rõ ràng. Ghé FPT Shop để trải nghiệm và chọn sản phẩm phù hợp, giúp việc học hiệu quả hơn ngay từ hôm nay.

Xem thêm: 

• Tìm hiểu công thức tính diện tích hình bình hành chuẩn xác và ví dụ minh họa chi tiết
• Dấu hiệu nhận biết hình chữ nhật: Kiến thức nền tảng trong toán hình học ở chương trình phổ thông