Chinh phục tam thức bậc 2: Tìm hiểu A đến Z từ định nghĩa, lý thuyết dấu đến bài toán ứng dụng

Tam thức bậc 2 là một trong những khái niệm nền tảng quan trọng trong toán học, đặc biệt là đại số. Nó xuất hiện trong nhiều lĩnh vực, từ giải phương trình, bất phương trình, đến khảo sát hàm số và ứng dụng trong các bài toán thực tế. Hiểu rõ về tam thức bậc 2 không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn mở ra cánh cửa khám phá những ứng dụng thú vị của toán học trong cuộc sống.

Lý thuyết của tam thức bậc 2

Tam thức bậc 2 là gì?

Tam thức bậc 2 xét theo biến số x là một dạng biểu thức toán học đặc biệt, có cấu trúc tổng quát là: ax² + bx + c.

Trong đó, a, b và c là các hệ số đã biết trước và điều kiện tiên quyết là a ≠ 0.

Các giá trị của x khi giải phương trình ax² + bx + c = 0 được xác định là nghiệm của tam thức bậc 2 này, ký hiệu là f(x) = ax² + bx + c. Để xác định số lượng và tính chất của nghiệm, ta sử dụng biệt thức (Δ) và biệt thức thu gọn (Δ') với công thức:

• Biệt thức: Δ = b² - 4ac.
• Biệt thức thu gọn: Δ' = b'² - ac (với b' = b/2).

Hai giá trị này giúp ta phân tích và giải quyết các bài toán liên quan đến tam thức bậc 2 một cách hiệu quả.

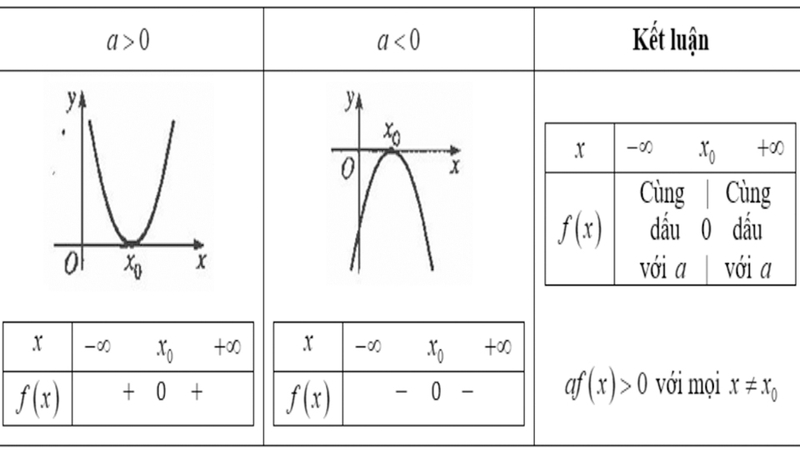
Dấu của tam thức bậc 2

Để hiểu rõ về dấu của tam thức bậc 2, chúng ta cần xem xét biểu thức f(x) = ax² + bx + c, trong đó a ≠ 0 và có biệt thức Δ = b² - 4ac.

Trường hợp Δ < 0: Khi biệt thức Δ âm, tam thức f(x) sẽ luôn mang cùng dấu với hệ số a, bất kể giá trị của x thuộc tập số thực R. Điều này có nghĩa là nếu a dương, f(x) luôn dương; nếu a âm thì f(x) luôn âm.

Trường hợp Δ = 0: Khi biệt thức Δ bằng 0, tam thức f(x) cũng sẽ luôn cùng dấu với hệ số a, ngoại trừ trường hợp x = -b/2a. Tại điểm này, f(x) sẽ bằng 0.

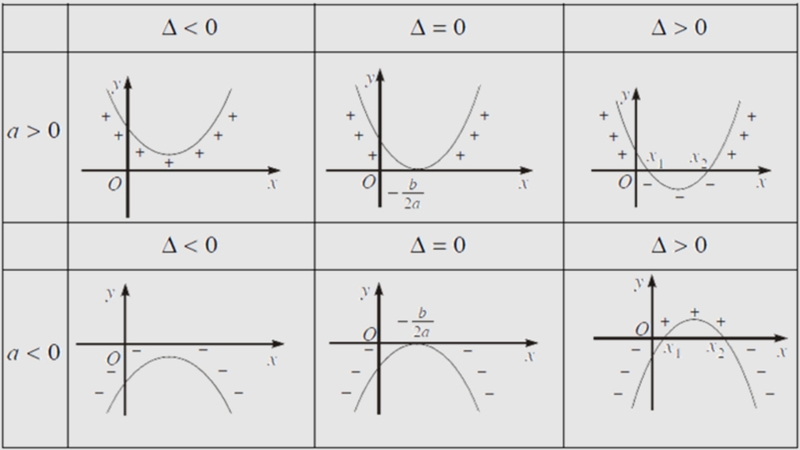
Trường hợp Δ > 0: Khi biệt thức Δ dương, tam thức f(x) sẽ có hai nghiệm phân biệt, ký hiệu là x₁ và x₂ (với x₁ < x₂). Trong trường hợp này:

• f(x) mang cùng dấu với hệ số a khi x nằm ngoài khoảng giữa hai nghiệm, tức là x < x₁ hoặc x > x₂.
• f(x) mang dấu ngược với hệ số a khi x nằm trong khoảng giữa hai nghiệm, tức là x₁ < x < x₂.

Mẹo nhớ nhanh:

Khi giải các bài toán về dấu của tam thức bậc 2 mà kết quả cho thấy phương trình có các nghiệm phân biệt, bạn có thể áp dụng quy tắc đơn giản để xác định dấu của biểu thức dựa trên mối quan hệ giữa dấu của hệ số a và dấu của tam thức f(x) trong các khoảng nghiệm:

• Trong khoảng giữa hai nghiệm: Giá trị của f(x) sẽ mang dấu trái ngược với dấu của hệ số a.
• Ngoài khoảng hai nghiệm: Giá trị của f(x) sẽ mang dấu tương tự như dấu của hệ số a.

Quy tắc trên giúp xác định dấu của tam thức bậc 2 trên các khoảng giá trị của x, điều này rất quan trọng trong việc giải bất phương trình và khảo sát hàm số.

Ví dụ: Xét tam thức bậc 2 có f(x) = x² - 4x + 4. 

Ta có a = 1, b = -4, c = 4 và Δ = (-4)² - 4 x 1 x 4 = 0. 

Nghiệm kép là x = -(-4) / (2 x 1) = 2. 

Do a = 1 > 0, nên f(x) luôn dương với mọi x ≠ 2 và f(2) = 0.

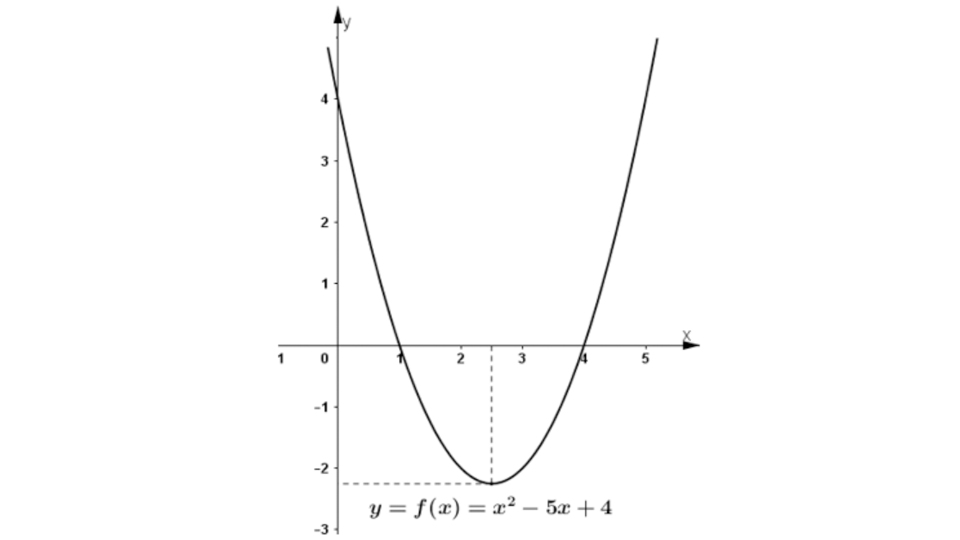
Đồ thị của tam thức bậc 2

Khi biểu diễn một tam thức bậc 2 dưới dạng đồ thị, ta sẽ thu được một đường cong đặc biệt gọi là parabol. Hình dáng của parabol này phụ thuộc hoàn toàn vào dấu của hệ số a trong biểu thức ax² + bx + c:

• Nếu a mang giá trị dương (a > 0), parabol sẽ có phần lõm hướng lên trên, tạo thành hình chữ "U".
• Nếu a mang giá trị âm (a < 0), parabol sẽ có phần lõm hướng xuống dưới, tạo thành hình chữ "∩".

Đỉnh của parabol: Đỉnh có tọa độ được xác định bởi công thức (-b/2a, -Δ/4a), trong đó Δ là biệt thức của tam thức bậc 2, được tính bằng b² - 4ac.

Trục đối xứng: Parabol có một trục đối xứng duy nhất là đường thẳng đi qua đỉnh và song song với trục tung. Phương trình của trục đối xứng này là x = -b/2a.

Hướng dẫn giải các dạng toán tam thức bậc 2

Chứng minh tam thức bậc 2 có nghiệm

Để chứng minh rằng một tam thức bậc 2 có nghiệm, bạn có thể sử dụng các phương pháp dựa trên các điều kiện về dấu của tam thức:

• Sử dụng giá trị đặc biệt: Nếu tồn tại một giá trị α sao cho tích αf(α) < 0, thì phương trình f(x) = 0 chắc chắn có hai nghiệm phân biệt. Nghĩa là khi thay giá trị α vào tam thức, thu được một giá trị có dấu ngược với dấu của α.
• Sử dụng hai giá trị khác nhau: Phương trình f(x) = 0 có hai nghiệm phân biệt nếu tồn tại hai giá trị α và β sao cho tích f(α)f(β) < 0 và a ≠ 0. Nghĩa là khi thay hai giá trị α và β vào tam thức, thu được hai giá trị có dấu ngược nhau.
• Chứng minh tồn tại nghiệm: Nếu tồn tại hai giá trị α và β sao cho tích f(α)f(β) < 0, thì phương trình f(x) = 0 có ít nhất một nghiệm. Đây là trường hợp tổng quát hơn của phương pháp trên, chỉ cần chứng minh có nghiệm, không nhất thiết là hai nghiệm phân biệt.

Ví dụ: Xét tam thức f(x) = x² - 4. 

Nếu chọn α = 1 và β = 3, thì f(1) = 1² - 4 = -3 và f(3) = 3² - 4 = 5. 

Tích f(1)f(3) = -3 * 5 = -15 < 0. 

Vậy tam thức f(x) = x² - 4 có hai nghiệm phân biệt.

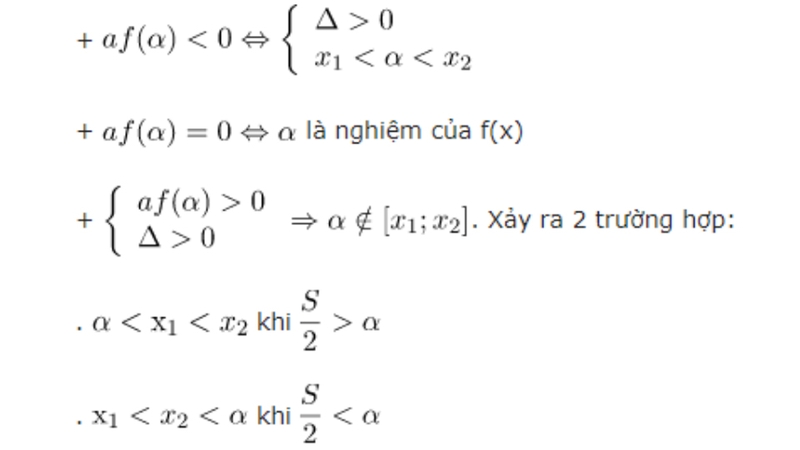
Xét dấu tam thức bậc 2

Để xét dấu của tam thức bậc hai f(x) = ax² + bx + c (với a ≠ 0), ta thực hiện theo các bước sau:

Tính biệt thức Δ: Tính Δ = b² - 4ac. Tìm nghiệm của tam thức (nếu có) bằng máy tính hoặc công thức nghiệm.

Lập bảng xét dấu: Dựa vào dấu của hệ số a và giá trị của Δ, lập bảng xét dấu theo các trường hợp sau:

• Δ < 0: f(x) luôn cùng dấu với a với mọi x ∈ R.
• Δ = 0: f(x) luôn cùng dấu với a với mọi x ∈ R, trừ x = -b/2a.
• Δ > 0: f(x) cùng dấu với a khi x < x₁ hoặc x > x₂, trái dấu với a khi x₁ < x < x₂.

Kết luận: Dựa vào bảng xét dấu, đưa ra kết luận về dấu của tam thức trên các khoảng giá trị của x.

Ví dụ minh họa: Xét dấu tam thức bậc 2 f(x) = x² - 3x + 2.

Ta có: Δ = (-3)² - 4 * 1 * 2 = 9 - 8 = 1 > 0. Nghiệm của tam thức là x₁ = 1 và x₂ = 2.

Với a = 1 > 0 và Δ > 0, nên ta có bảng xét dấu sau:

Từ bảng xét dấu, ta có:

• f(x) > 0 khi x < 1 hoặc x > 2.
• f(x) < 0 khi 1 < x < 2.
• f(1) = f(2) = 0.

Vậy tam thức bậc 2 f(x) = x² - 3x + 2 dương trên khoảng (-∞;1) và (2;+∞) và âm trên khoảng (1;2).

Bài tập tự luyện tam thức bậc 2 có hướng dẫn

Để nắm rõ và ghi nhớ các tính chất, hãy chủ động luyện tập qua một số bài toán về tam thức bậc 2 từ cơ bản đến nâng cao sau:

Câu 1: Xét dấu tam thức f(x) = x² - 5x + 6.

(Gợi ý: Tìm nghiệm, lập bảng xét dấu "trong trái, ngoài cùng")

Câu 2: Chứng minh tam thức g(x) = x² + 2x - 3 có nghiệm.

(Gợi ý: Tính Δ, nếu Δ > 0 thì có 2 nghiệm phân biệt)

Câu 3: Xét dấu tam thức h(x) = -2x² + 4x - 2.

(Gợi ý: Tìm nghiệm kép, xét dấu theo hệ số a trừ nghiệm kép)

Câu 4: Cho tam thức f(x) = x² - mx + 1. Tìm m để f(x) có nghiệm.

(Gợi ý: Tính Δ theo m, giải bất phương trình Δ ≥ 0)

Câu 5: Xét dấu f(x) = x² - 4x + 3 trên khoảng (0;5).

(Gợi ý: Tìm nghiệm, lập bảng xét dấu trên khoảng đã cho)

Câu 6: Chứng minh x² + x + 1 > 0 với mọi x thuộc R.

(Gợi ý: Chứng minh Δ < 0 và hệ số a > 0)

Tạm kết

Tam thức bậc 2 là một dạng toán thường gặp và được ứng dụng nhiều trong thực tế. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hy vọng bài viết đã phần nào giúp bạn chinh phục mọi bài toán liên quan đến tam thức bậc 2.

Bạn đang tìm kiếm một chiếc laptop vừa mạnh mẽ để học tập, vừa giải trí mượt mà? Đừng bỏ lỡ cơ hội sở hữu laptop Dell với cấu hình vượt trội, thiết kế thời trang và độ bền bỉ đáng tin cậy. Đặc biệt, FPT Shop đang có chương trình ưu đãi hấp dẫn dành riêng cho học sinh, sinh viên với nhiều quà tặng giá trị và chính sách trả góp linh hoạt. Khám phá thêm về laptop Dell tại đây:

Laptop Dell

Xem thêm:

• Top 9 web giải toán online cực chuẩn xác, nhanh chóng và miễn phí
• Tổng hợp đầy đủ công thức lượng giác dễ hiểu, dễ nhớ dành cho học sinh từ lớp 9 đến lớp 11