Tổng quan về nhị thức Newton lớp 10 và tổng hợp các dạng bài tập, ứng dụng thường gặp

Khai triển nhị thức Newton là một trong những kiến thức quan trọng của môn Đại số, giúp chúng ta biểu diễn lũy thừa của một nhị thức thành một tổng gồm nhiều hạng tử, mỗi hạng có hệ số riêng. Trong chương trình Toán lớp 10, công thức này không chỉ giúp rút ngắn thời gian tính toán mà còn được ứng dụng nhiều trong các bài toán tổ hợp và xác suất. Ở bài viết này, FPT Shop sẽ cùng bạn khám phá cách sử dụng nhị thức Newton lớp 10 hiệu quả kèm theo một số bài tập minh họa để bạn dễ dàng hiểu và vận dụng trong học tập.

Tổng quan về nhị thức Newton lớp 10

Khai triển nhị thức Newton là một công cụ quen thuộc và rất hữu ích trong Toán học, đặc biệt khi làm việc với các biểu thức có dạng lũy thừa của một tổng. Công thức này cho phép ta viết biểu thức: (a+b)n thành một tổng gồm nhiều hạng tử, trong đó mỗi hạng đều có hệ số riêng – chính là các số tổ hợp. 

Nếu bạn muốn hiểu rõ hơn về cách khai triển này hoạt động, hãy cùng FPT Shop khám phá chi tiết định lý nhị thức Newton lớp 10. Đây là một phần kiến thức cơ bản nhưng rất quan trọng trong đại số, không chỉ giúp việc tính toán trở nên dễ dàng hơn mà còn được ứng dụng trong nhiều chủ đề khác như tổ hợp, xác suất,... Dưới đây là cách trình bày cụ thể và đầy đủ của công thức này để bạn tiện theo dõi và áp dụng.

Công thức nhị thức Newton lớp 10 giúp chúng ta viết gọn biểu thức lũy thừa của một tổng thành một dãy các hạng tử với hệ số được xác định rõ ràng, dễ tính. Nhờ vậy, những phép toán tưởng chừng phức tạp cũng trở nên nhẹ nhàng hơn. Đây cũng là một nền tảng quan trọng được ứng dụng rộng rãi trong nhiều mảng kiến thức Toán học khác.

Công thức khai triển nhị thức Newton

Trong Toán học, khi cần xử lý lũy thừa của một nhị thức, chúng ta có một công cụ cực kỳ hữu ích – đó là công thức khai triển nhị thức Newton. Đây là một phương pháp quen thuộc giúp biến những biểu thức phức tạp thành một tổng gồm nhiều hạng tử cụ thể, mỗi hạng tử được xác định dựa trên hệ số tổ hợp. Nhờ đó, việc tính toán trở nên nhanh chóng, rõ ràng và dễ hiểu hơn. Ngay sau đây là cách áp dụng công thức này mà bạn có thể tham khảo và thực hành.

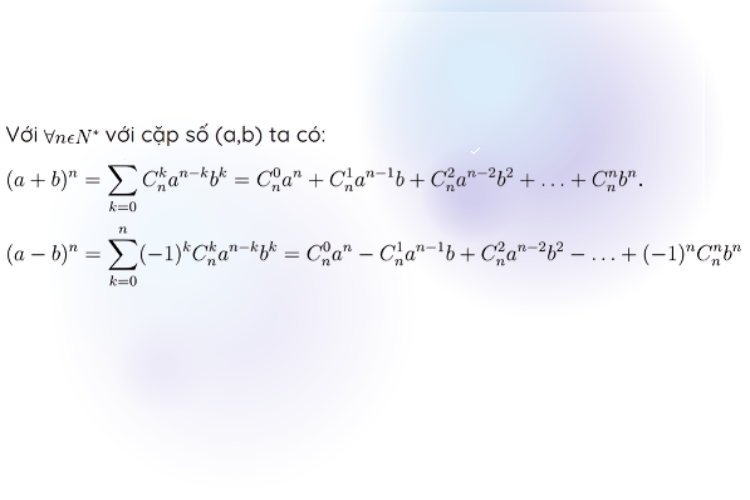
Các dạng bài tập về nhị thức Newton

Nhị thức Newton là một trong những công thức quan trọng trong Toán học, không chỉ giúp đơn giản hóa các biểu thức phức tạp mà còn đóng vai trò là nền tảng cho nhiều lĩnh vực liên quan. Để nắm vững và sử dụng thành thạo công thức này, học sinh cần luyện tập qua nhiều dạng bài khác nhau. Dưới đây là một số bài tập minh họa giúp bạn rèn luyện kỹ năng khai triển, tìm hệ số cũng như xác định số hạng tổng quát một cách hiệu quả.

Cách tìm hệ số và số hạng trong khai triển nhị thức

Ở dạng bài này, điều quan trọng là xác định được số hạng tổng quát trong khai triển, thường được gọi là số hạng thứ  k+1. Việc này giúp ta dễ dàng phân tích và tìm ra hệ số hoặc phần chứa biến theo yêu cầu.

Cách làm cụ thể như sau:

Bắt đầu bằng việc viết công thức khai triển tổng quát của nhị thức dạng (a+b)n

Từ đó, xác định biểu thức của số hạng thứ  k+1 dựa trên công thức tổ hợp. Sau khi có biểu thức, ta tách riêng phần chứa biến và hệ số.

Cuối cùng, dùng điều kiện của đề bài (chẳng hạn yêu cầu tìm hệ số của một lũy thừa cụ thể của biến) để tìm giá trị k phù hợp. Nhớ rằng mỗi số hạng trong khai triển đều bao gồm hai phần: phần hệ số (gắn với tổ hợp) và phần biến (gắn với lũy thừa).

Ví dụ 1: Hệ số của x^31 trong khai triển [x + (1/x^2)]^40 là bao nhiêu? Hướng dẫn giải

Ví dụ 2: Tìm số hạng không có x trong khai triển của nhị thức sau: [x + (1/x)]^12. Hướng dẫn giải:

Ứng dụng trong rút gọn và chứng minh biểu thức

Để chứng minh hoặc rút gọn biểu thức bằng phương pháp nhị thức Newton, trước hết ta cần phân tích kỹ đề bài để xác định một hàm phù hợp với tổng hoặc bất đẳng thức cần xử lý. Một số dạng hàm thường được sử dụng bao gồm: (x + 1)^n, (1 + x)^n, (1 - x)^n, (x - 1)^n.

Sau đó, tiến hành khai triển nhị thức Newton và áp dụng các phép biến đổi đại số cùng với các kỹ thuật giải tích cần thiết để đơn giản hóa biểu thức, đưa về dạng dễ quan sát và dễ hiểu.

Trong quá trình đơn giản hóa, ta thường lựa chọn giá trị cụ thể cho x, phổ biến là x = 1 hoặc x = -1 (đôi khi có thể là ±2, ±3...), nhằm làm cho biểu thức trở nên đơn giản hơn. Từ các bước khai triển và biến đổi đó, ta có thể suy ra tổng hoặc khẳng định cần chứng minh một cách rõ ràng và logic.

Ví dụ

Áp dụng trong việc giải các phương trình và bất phương trình có yếu tố tổ hợp, chỉnh hợp

Khi gặp những bài toán có liên quan đến tổ hợp hoặc chỉnh hợp, ta thường phải vận dụng kiến thức về đếm như hoán vị, tổ hợp, chỉnh hợp để đơn giản hóa biểu thức. Việc này giúp chuyển bài toán ban đầu về một dạng dễ xử lý hơn.

Sau khi rút gọn, bước tiếp theo là xem xét điều kiện để nghiệm thỏa mãn, từ đó xác định kết quả đúng. Sự kết hợp giữa kiến thức tổ hợp và các kỹ năng đại số không chỉ giúp giải các bài toán lý thuyết mà còn rất hữu ích trong việc xử lý các tình huống phân bố, sắp xếp trong thực tế.

Lời kết

Khai triển nhị thức Newton là một công cụ Toán học quan trọng, hỗ trợ hiệu quả trong việc giải các bài toán về đại số, tổ hợp và xác suất. Việc thành thạo công thức cùng các dạng bài tập liên quan không chỉ giúp học sinh phát triển tư duy logic mà còn nâng cao khả năng ứng dụng vào thực tiễn. Qua bài viết này, hy vọng bạn đã nắm vững hơn về khai triển nhị thức Newton lớp 10 và có thể vận dụng nó hiệu quả trong quá trình học tập.

Nếu bạn đang tìm mua laptop phục vụ cho công việc hay học tập, đừng ngần ngại ghé ngay FPT Shop để được tư vấn tận tình và lựa chọn sản phẩm phù hợp. Tại đây, bạn sẽ được trải nghiệm đa dạng mẫu mã, giá cả hợp lý, nhiều ưu đãi hấp dẫn cùng chính sách trả góp 0% tiện lợi, giúp bạn dễ dàng sở hữu chiếc laptop mong muốn mà không lo áp lực tài chính.

Tham khảo thêm tại đây: Máy tính xách tay

Xem thêm

• Nắm ngay công thức tính CPI đơn giản, chính xác nhất để tính chỉ số giá tiêu dùng
• Tìm hiểu công thức tính công cơ học chuẩn xác và các kiến thức quan trọng nên biết