Đường trung trực là gì? Khám phá định nghĩa, tính chất và những dạng bài tập minh họa hay nhất

Không chỉ là một đường thẳng vuông góc đi qua trung điểm của một đoạn thẳng, đường trung trực còn mở ra nhiều điều thú vị về tính đối xứng, sự cân bằng và các mối quan hệ hình học. Hãy cùng khám phá sâu hơn về khái niệm tưởng chừng quen thuộc này để dễ dàng chinh phục toán học và cuộc sống.

Khái niệm và định nghĩa đường trung trực

Khái niệm

Đường trung trực là đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó. Điều này có nghĩa là đường trung trực chia đoạn thẳng thành hai phần bằng nhau và tạo thành một góc 90 độ với đoạn thẳng đó.

Không chỉ quan trọng trong lý thuyết hình học, khái niệm này còn được ứng dụng nhiều trong thực tế ở lĩnh vực như xây dựng, thiết kế và kỹ thuật. Chẳng hạn trong xây dựng, đường trung trực có thể được sử dụng để xác định vị trí của các cột hoặc tường sao cho chúng cách đều hai điểm mốc. Trong thiết kế, đường trung trực được sử dụng để tạo ra các hình dạng đối xứng.

Định nghĩa

Cho đoạn thẳng AB, đường trung trực của AB là đường thẳng d vuông góc với AB tại điểm M, với M là trung điểm của AB. Nói cách khác, đường thẳng d đi qua điểm M và tạo thành một góc vuông với đoạn thẳng AB. Với định nghĩa này, ta có thể dễ dàng xác định và vẽ đường trung trực của bất kỳ đoạn thẳng nào.

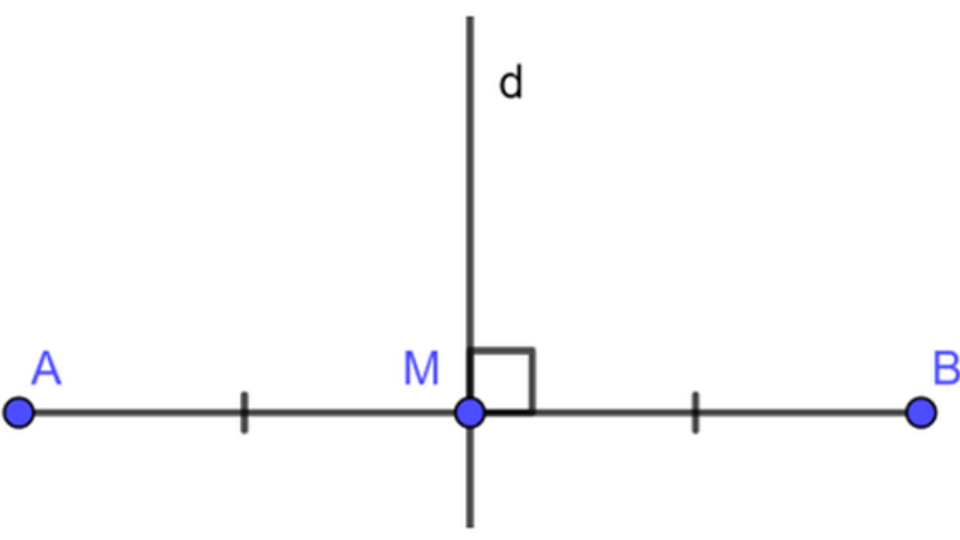
Đường trung trực có tính chất gì đặc biệt?

Đối với đoạn thẳng

Đường trung trực có 2 tính chất chính bạn cần nằm lòng đó là:

Tính chất 1: Nếu một điểm nằm trên đường trung trực của một đoạn thẳng, điểm đó sẽ luôn cách đều hai đầu mút của đoạn thẳng đó.

Ví dụ: Giả sử đường thẳng "d" là đường trung trực của đoạn thẳng AB. Nếu ta chọn một điểm N bất kỳ nằm trên đường thẳng "d" (N ∈ d), thì khoảng cách từ N đến A (NA) sẽ luôn bằng khoảng cách từ N đến B (NB). Điều này có nghĩa là NA = NB.

Tính chất này rất quan trọng trong việc xác định vị trí tương đối của các điểm so với một đoạn thẳng.

Tính chất 2: Nếu một điểm cách đều hai đầu mút của đoạn thẳng, điểm này chắc chắn sẽ nằm trên đường trung trực của đoạn thẳng đó.

Ví dụ: Ta chứng minh được rằng một điểm M nào đó có khoảng cách đến A (MA) bằng khoảng cách đến B (MB) (MA = MB), thì có thể kết luận rằng điểm M nằm trên đường trung trực của đoạn thẳng AB.

Tính chất này giúp xác định đường trung trực khi biết các điểm cách đều. Vì vậy có thể nói tập hợp những điểm cách đều nằm tại hai mút của một đoạn thẳng chính là đường trung trực của đoạn thẳng đó.

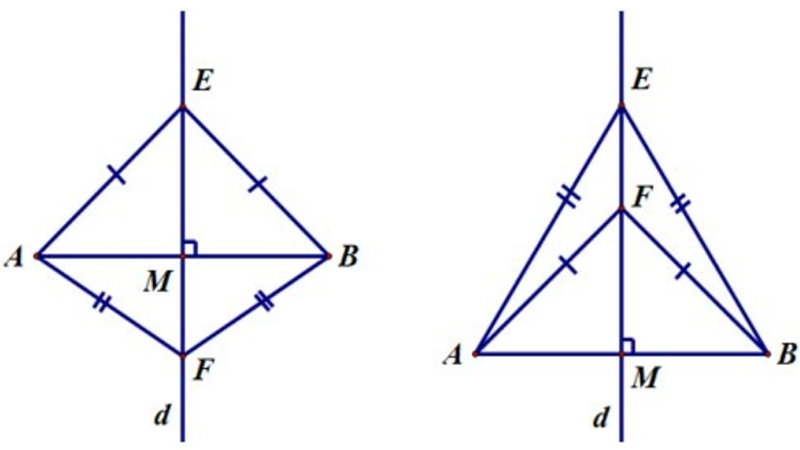Đối với hình tam giác

Tam giác thường: Trong một tam giác bất kỳ, ba đường trung trực của ba cạnh luôn giao nhau tại một điểm duy nhất. Điểm này có một vị trí đặc biệt - nó cách đều ba đỉnh của tam giác.

• Điểm đồng quy: Gọi giao điểm của ba đường trung trực là O. Khi đó, ta có OA = OB = OC.
• Đường tròn ngoại tiếp: Điều này có nghĩa là điểm O chính là tâm của đường tròn đi qua ba đỉnh của tam giác, hay còn gọi là đường tròn ngoại tiếp tam giác đó.

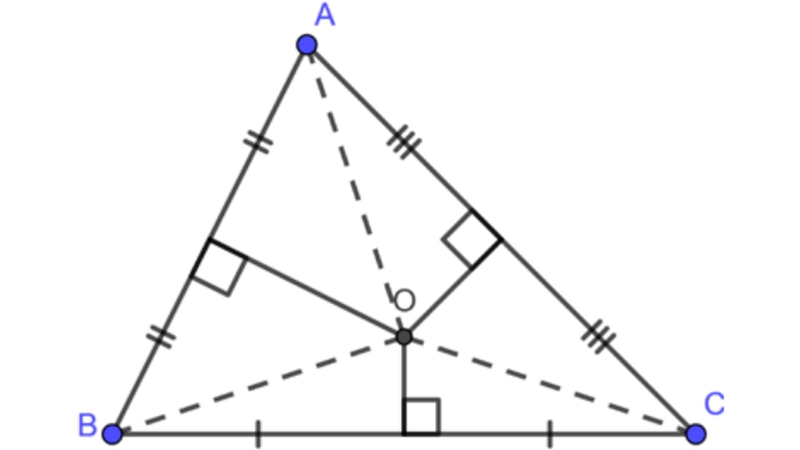
Tam giác vuông: Giao điểm của ba đường trung trực trong tam giác vuông trùng với trung điểm của cạnh huyền.

• Vị trí đặc biệt: Xét tam giác ABC vuông tại B. Giao điểm của ba đường trung trực (gọi là E), chính là trung điểm của cạnh AC (cạnh huyền).
• Hệ quả: Do đó, EA = EB = EC. Điều này có nghĩa là trung điểm cạnh huyền cũng chính là tâm đường tròn ngoại tiếp tam giác vuông đó.

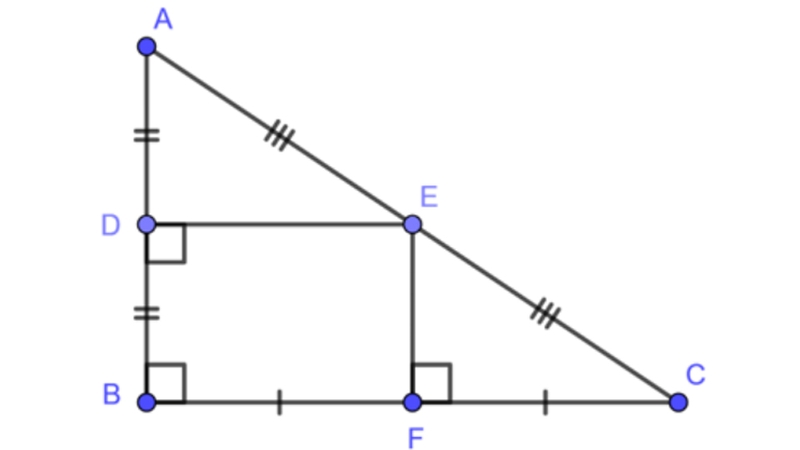
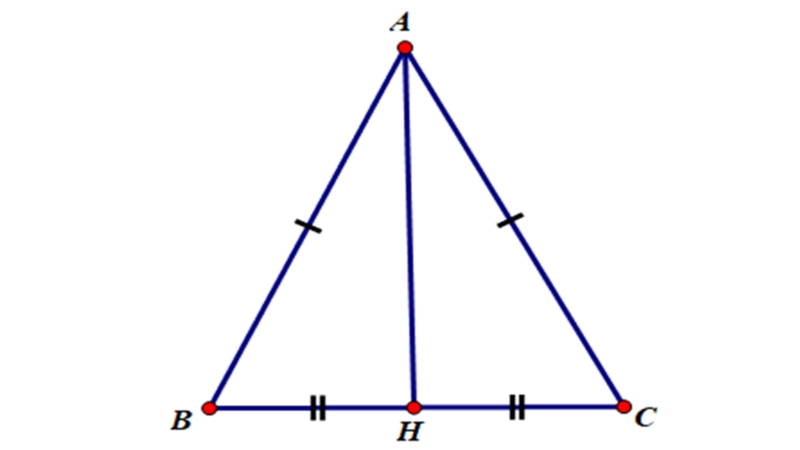
Tam giác cân: Đường trung trực ứng với cạnh đáy vừa đồng thời là đường phân giác, đường trung tuyến và đường cao xuất phát từ đỉnh đối diện với cạnh đáy đó.

• Tính trùng khớp: Xét tam giác ABC cân tại A. Đường trung trực của cạnh BC cũng là đường phân giác góc A, đường trung tuyến kẻ từ A và đường cao kẻ từ A.
• Tính đối xứng: Tính chất này thể hiện sự đối xứng tuyệt vời của tam giác cân, giúp giải quyết nhiều bài toán hình học một cách đơn giản.

Cách xác định hoặc vẽ đường trung trực đơn giản

a, Chuẩn bị dụng cụ: Thước kẻ, compas (hoặc thước đo độ dài), bút chì.

b, Thực hiện xác định trung điểm trên đoạn thẳng:

Gọi đoạn thẳng cần xác định đường trung trực là AB, để tìm trung điểm trên AB, bạn thực hiện một trong hai cách sau:

Cách 1: Sử dụng thước kẻ

Đo độ dài đoạn thẳng AB, sau đó chia đôi để tìm và đánh dấu trung điểm.

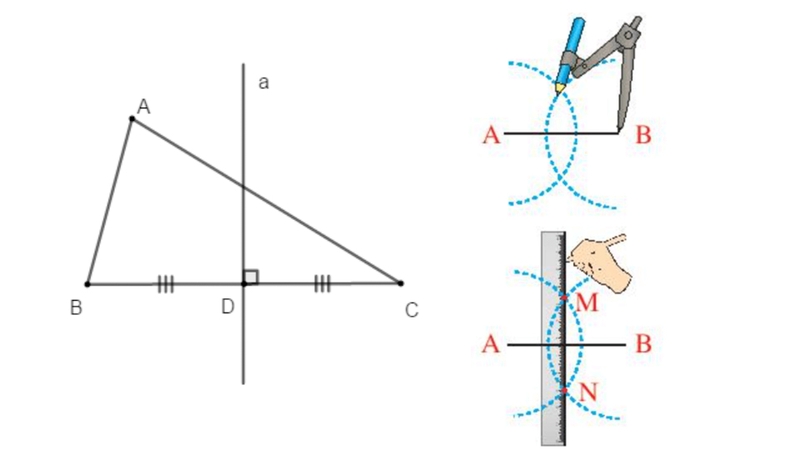
Cách 2: Sử dụng compas

• Đặt đầu nhọn của compas vào điểm A, mở rộng compas sao cho bán kính lớn hơn một nửa độ dài đoạn thẳng AB.
• Vẽ một cung tròn.
• Giữ nguyên bán kính, đặt đầu nhọn của compas vào điểm B và vẽ một cung tròn khác, cắt cung tròn thứ nhất tại hai điểm.
• Nối 2 điểm giao nhau của 2 cung tròn, giao điểm của đường nối 2 điểm giao nhau đó và đoạn thẳng AB chính là trung điểm cần tìm.

c, Kẻ đường thẳng d vuông góc với đoạn thẳng AB tại điểm M: 

Sử dụng thước kẻ và bút chì, đặt sao cho cạnh thước vuông góc với đoạn thẳng AB cắt tại trung điểm vừa đánh dấu. Kẻ một đường thẳng đi qua điểm đó và vuông góc với AB. Đường thẳng này được gọi là đường trung trực d của đoạn thẳng AB.

Một số dạng toán đường trung trực và cách giải quyết

Bài toán chứng minh đường trung trực

Để chứng minh một đường thẳng là đường trung trực của một đoạn thẳng, ta cần chứng minh đường thẳng đó thỏa mãn 2 điều kiện:

• Đường thẳng đi qua và vuông góc tại trung điểm của đoạn thẳng.
• Chứa hai điểm cách đều hai đầu mút của đoạn thẳng đó.

Hoặc có thể dùng định nghĩa đường trung trực để chứng minh đường thẳng đó vuông góc với đoạn thẳng tại trung điểm.

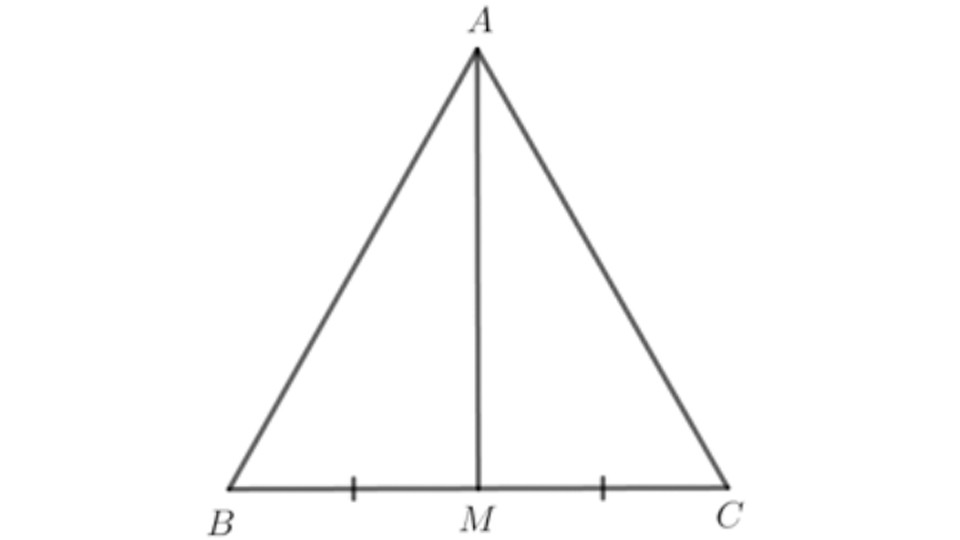
Ví dụ: Cho tam giác ABC cân tại A, với M là trung điểm của cạnh BC. Ta cần chứng minh rằng AM là đường trung trực của BC.

Giải:

Do tam giác ABC cân tại A, ta có AB = AC (theo tính chất tam giác cân).
Vì M là trung điểm của BC, nên ta suy ra MB = MC (theo định nghĩa trung điểm).

Xét hai tam giác AMB và AMC, ta có:

• AB = AC (giả thiết tam giác cân)
• MB = MC (M là trung điểm của BC)
• AM là cạnh chung

Từ đó, theo trường hợp bằng nhau cạnh-cạnh-cạnh (CCC), ta suy ra tam giác AMB = tam giác AMC.
Vì hai tam giác này bằng nhau, ta có góc AMB = góc AMC.

Mặt khác, tổng hai góc AMB và AMC là 180° (hai góc kề bù), nên mỗi góc bằng 90°.
Do đó, AM vuông góc với BC tại M. Vì M là trung điểm của BC, ta kết luận rằng AM là đường trung trực của BC.

Bài toán tâm đường tròn ngoại tiếp

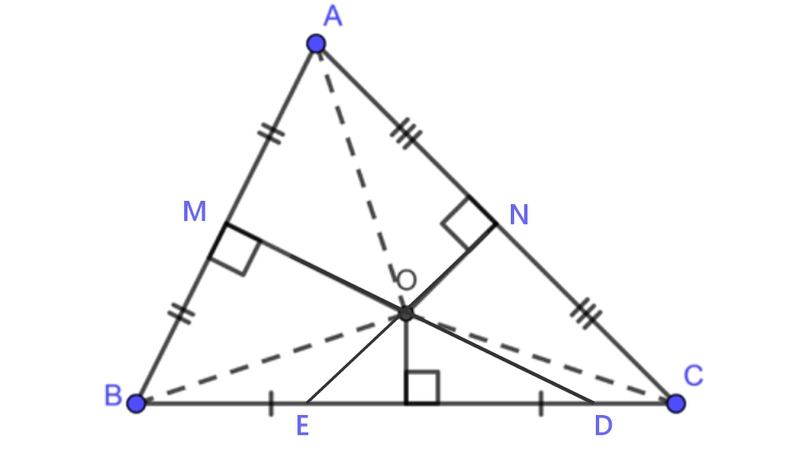
Trong dạng bài toán tìm tâm đường tròn ngoại tiếp, cần áp dụng tính chất của đường trung trực trong tam giác: Ba đường trung trực của tam giác luôn cắt nhau tại một điểm duy nhất và điểm này có khoảng cách bằng nhau đến cả ba đỉnh của tam giác.

Ví dụ: Xác định tâm đường tròn ngoại tiếp của tam giác ABC.

Giải:

Đầu tiên, vẽ đường trung trực của hai cạnh AB và AC. Kéo dài hai đường trung trực, giao điểm chính là tâm đường tròn ngoại tiếp của tam giác ABC.

Bài toán chứng minh hai đoạn thẳng bằng nhau

Phương pháp để giải dạng toán có yêu cầu này là sử dụng định lý đường trung trực: Điểm nằm trên đường trung trực luôn cách đều hai mút của đoạn thẳng đó.

Ví dụ: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của hai đoạn AB và AC. Từ đó có đường trung trực của AB, AC cắt BC tại D và E. Chứng minh rằng DA = DB và EA = EC.

Giải:

Dựa vào định lý của đường trung trực:

Vì DM là đường trung trực của cạnh AB nên DA = DB => Tam giác ADB cân tại D.

Vì EN là đường trung trực của cạnh AC nên EA = EC => Tam giác AEC cân tại E.

Bài toán về giá trị bé nhất

Để giải quyết bài toán này, bạn có thể áp dụng tính chất của đường trung trực để thay thế độ dài của một đoạn thẳng bằng độ dài của đoạn thẳng khác có độ dài tương đương. Đồng thời, sử dụng bất đẳng thức tam giác để xác định giá trị nhỏ nhất, với điều kiện tổng của hai cạnh bất kỳ luôn lớn hơn cạnh còn lại và hiệu của hai cạnh bất kỳ luôn nhỏ hơn cạnh còn lại.

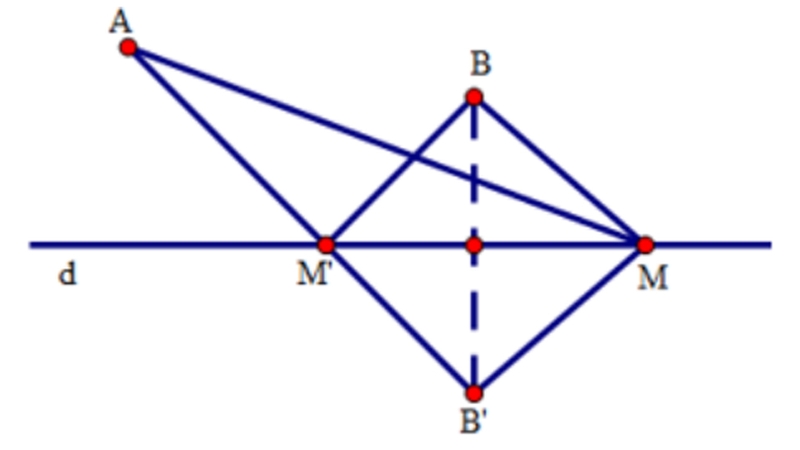
Ví dụ: Cho hai điểm A, B nằm trên nửa mặt phẳng bờ d. Tìm trên d điểm M sao cho MA + MB có giá trị nhỏ nhất.

Giải:

Qua d, ta vẽ điểm A' đối xứng với điểm A. Khi đó, d là đường trung trực của đoạn thẳng AA'. Theo tính chất đường trung trực, mọi điểm nằm trên đường trung trực đều cách đều hai đầu mút của đoạn thẳng đó. Do đó, MA = MA'.

Ta có: MA + MB = MA' + MB.

Xét tam giác A'MB, theo bất đẳng thức tam giác, ta có: MA' + MB ≥ A'B.

Dấu "=" xảy ra khi và chỉ khi ba điểm A', B, M thẳng hàng.

Vậy MA + MB đạt giá trị nhỏ nhất khi M là giao điểm của đường thẳng A'B và đường thẳng d. Giá trị nhỏ nhất của MA + MB là A'B.

Bài toán đường trung trực trong tam giác vuông

Đây là một dạng bài toán về đường trung trực rất thường thấy, để giải được thì bạn cần nắm tính chất: Trong tam giác vuông, giao điểm các đường trung trực là trung điểm cạnh huyền.

Ví dụ: Cho tam giác ABC vuông tại A, cạnh BC = 10cm. Tính khoảng cách từ giao điểm 3 đường trung trực tới các đỉnh của tam giác.

Giải:

Gọi O là giao điểm của 3 đường trung trực, vì tam giác ABC vuông tại A nên O là trung điểm cạnh BC. Dựa trên tính chất của đường trung trực trong tam giác vuông, ta có:

OB = OC = OA = BC/2 = 5(cm).

Bài toán đường trung trực trong tam giác cân

Bạn cần nhớ rằng, trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến, đường phân giác ứng với cạnh đáy này để áp dụng.

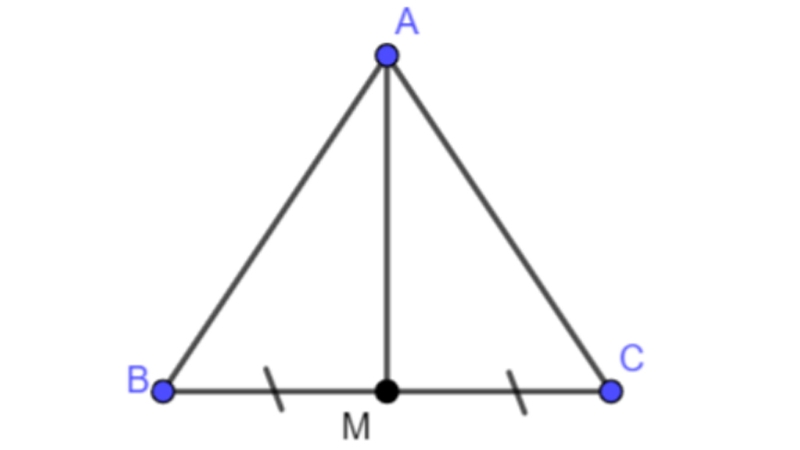
Ví dụ: Cho tam giác ABC cân tại A, M là trung điểm của cạnh BC. Chứng minh rằng AM là tia phân giác của góc BAC.

Giải:

Vì tam giác ABC cân tại A nên AM là đường trung tuyến.

Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy cũng chính là đường phân giác.

Do đó, góc BAC có AM là phân giác.

Một số bài tập tự luyện về đường trung trực

Bài 1: Cho đoạn thẳng AB có đường trung trực d. Lấy điểm M bất kỳ trên d. Chứng minh rằng MA = MB.

(Gợi ý: Sử dụng tính chất điểm nằm trên đường trung trực cách đều hai đầu đoạn thẳng)

Bài 2: Cho tam giác ABC cân tại A với M là trung điểm trên BC. Chứng minh rằng đường thẳng AM vuông góc và đi qua trung điểm của đoạn BC.

(Gợi ý: Chứng minh AM vuông góc với BC và M là trung điểm BC)

Bài 3: Cho tam giác ABC, vẽ đường trung trực của hai cạnh AB và AC, chúng cắt nhau tại O. Chứng minh điểm O cách đều ba đỉnh của tam giác.

(Gợi ý: Chứng minh OA = OB và OA = OC, suy ra OB = OC)

Bài 4: Cho tam giác ABC vuông tại A, trên cạnh BC có M là trung điểm. Chứng minh rằng AM = BM = CM.

(Gợi ý: Chứng minh M là giao điểm ba đường trung trực của tam giác ABC)

Bài 5: Cho tam giác ABC. Vẽ đường trung trực của các cạnh AB, BC, CA, chúng cắt nhau tại O. Chứng minh rằng ba điểm A, B, C nằm trên một đường tròn tâm O.

(Gợi ý: Chứng minh OA = OB = OC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC)

Bài 6: Cho đường thẳng d có điểm A và B nằm về hai phía. Tìm điểm M trên đường thẳng d sao cho MA + MB có giá trị nhỏ nhất.

(Gợi ý: Lấy A' đối xứng với A qua d. Chứng minh MA + MB = MA' + MB ≥ A'B. M đạt giá trị nhỏ nhất khi M là giao điểm của A'B và d.)

Tạm kết

Có thể khẳng định, đường trung trực là một khái niệm quan trọng và hữu ích trong hình học, với nhiều ứng dụng trong cả lý thuyết và thực tiễn. Việc nắm vững kiến thức về đường trung trực sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn.

Bạn muốn sở hữu một chiếc laptop chất lượng sử dụng cho việc học online hoặc giải trí thả ga sau giờ học? Hãy tham khảo ngay dòng laptop Lenovo với cấu hình mạnh mẽ, thiết kế thời trang và giá cả cực kỳ hấp dẫn. Ghé FPT Shop sớm nhất để trải nghiệm và rinh về cho mình chiếc laptop Lenovo ưng ý nhất nhé! Xem các dòng máy tính xách tay chất lượng dưới đây:

Laptop Lenovo

Xem thêm:

• Tìm hiểu công thức tính công cơ học chuẩn xác và các kiến thức quan trọng nên biết
• Tìm hiểu công thức tính diện tích hình bình hành chuẩn xác và ví dụ minh họa chi tiết