Đồng quy là gì? Khám phá khái niệm, phương pháp chứng minh và những ví dụ cụ thể

Đồng quy là một khái niệm quan trọng trong hình học. Trong bài viết này, chúng ta sẽ cùng tìm hiểu đồng quy là gì, làm thế nào để chứng minh hiện tượng này và các ví dụ cụ thể. Mời bạn theo dõi!

Đồng quy là gì?

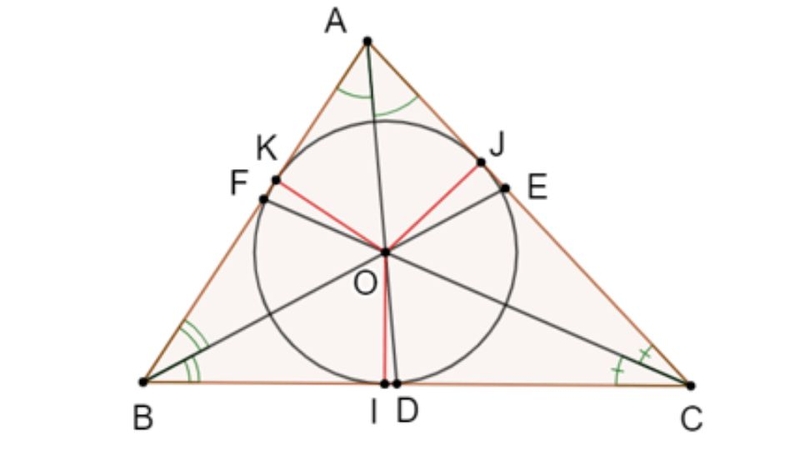
Đồng quy là thuật ngữ dùng để chỉ hiện tượng ba hoặc nhiều đường thẳng cắt nhau tại một điểm duy nhất, được gọi là điểm đồng quy. Đây là một tính chất cơ bản nhưng quan trọng trong cả hình học phẳng và hình học không gian, đóng vai trò then chốt trong việc phân tích và chứng minh các bài toán hình học. 

Đồng quy thường xuất hiện trong các bài toán liên quan đến tam giác và hệ đường thẳng, đặc biệt hữu ích trong việc phát hiện và thiết lập mối liên hệ giữa các yếu tố hình học. Ngoài phạm vi lý thuyết, khái niệm này còn có ứng dụng thực tiễn trong nhiều lĩnh vực như kiến trúc, thiết kế kết cấu hay quy hoạch giao thông vì trong các lĩnh vực này thì việc xác định các giao điểm chính xác đóng vai trò quan trọng trong thiết kế và triển khai.

Những trường hợp đồng quy phổ biến

Chúng ta đã cùng tìm hiểu đồng quy là gì qua phần nội dung trên. Khái niệm đồng quy không chỉ giới hạn trong các yếu tố của tam giác mà còn xuất hiện trong nhiều dạng hình học khác nhau như đường tròn, tứ giác và trong không gian ba chiều. Hiện tượng này thể hiện sự giao nhau tại một điểm duy nhất của ba hoặc nhiều đường thẳng và thường được khai thác trong nhiều bài toán hình học. Dưới đây là một số trường hợp đồng quy phổ biến:

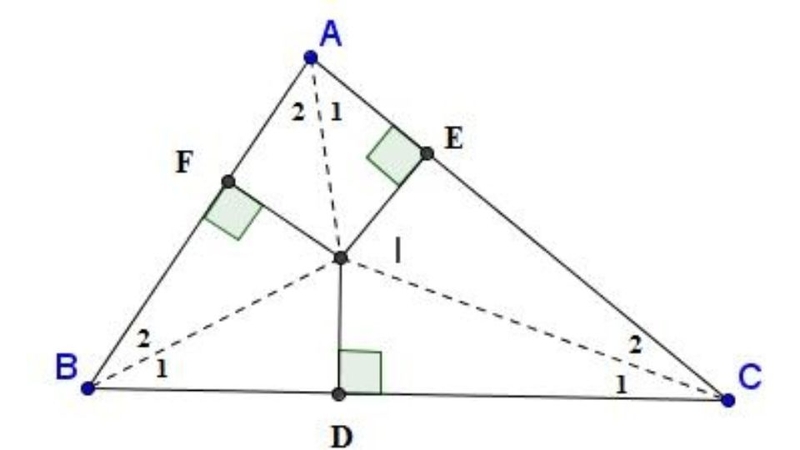
• Trong tam giác: Có nhiều bộ ba đường thẳng cùng đi qua một điểm như ba đường trung tuyến giao nhau tại trọng tâm, ba đường phân giác gặp nhau tại tâm đường tròn nội tiếp, ba đường trung trực đồng quy tại tâm đường tròn ngoại tiếp và ba đường cao cắt nhau tại trực tâm.
• Trong đường tròn: Tất cả các đường kính của một đường tròn đều đi qua tâm đường tròn nên chúng đồng quy tại đó. Ngoài ra, nếu xét các tiếp tuyến tại một điểm trên đường tròn (trong không gian ba chiều), các tiếp tuyến nằm trên cùng mặt phẳng cũng có thể hội tụ tại một điểm khi mở rộng theo điều kiện bài toán.

Tổng hợp phương pháp chứng minh đồng quy

Việc chứng minh ba (hoặc nhiều) đường thẳng đồng quy, tức là cùng đi qua một điểm duy nhất, có thể được thực hiện bằng nhiều phương pháp khác nhau tùy vào từng bài toán cụ thể. Vậy các phương pháp chứng minh đồng quy là gì?

Phương pháp 1: Tìm điểm giao của hai đường rồi kiểm tra đường còn lại

Xác định điểm cắt nhau của hai trong ba đường cần xét. Sau đó, chứng minh rằng đường thẳng thứ ba cũng đi qua điểm này. Nếu đúng thì ba đường thẳng đồng quy tại điểm đó.

Phương pháp 2: Chứng minh một điểm nằm trên cả ba đường thẳng

Lựa chọn một điểm cụ thể (có thể được gợi ý từ giả thiết hoặc hình vẽ) và chứng minh rằng điểm đó nằm trên cả ba đường. Khi đó, ba đường thẳng đồng quy tại điểm ấy.

Phương pháp 3: Sử dụng các tính chất đồng quy trong tam giác

Áp dụng những định lý quen thuộc như: ba đường trung tuyến đồng quy tại trọng tâm, ba đường cao tại trực tâm, ba đường phân giác trong tại tâm đường tròn nội tiếp,...

Phương pháp 4: Khai thác quan hệ hình học đặc biệt

Sử dụng mối quan hệ giữa các đường song song, giao điểm hoặc các đoạn thẳng có tỷ lệ đặc biệt (chẳng hạn như định lý Thales, đồng dạng tam giác,...) để suy ra tính đồng quy.

Phương pháp 5: Phản chứng (chứng minh bằng mâu thuẫn)

Giả sử ba đường không đồng quy (tức là không cùng đi qua một điểm), sau đó chỉ ra giả định này dẫn đến mâu thuẫn với giả thiết, kết luận hoặc tính chất đã biết. Khi đó, ta khẳng định ba đường là đồng quy.

Phương pháp 6: Dựa vào tính chất thẳng hàng

Xét ba điểm lần lượt thuộc ba đường thẳng cần chứng minh và chỉ ra rằng ba điểm này thẳng hàng. Từ đó suy ra ba đường thẳng cắt nhau tại một điểm duy nhất.

Phương pháp 7: Chứng minh trực tiếp cả ba đường đi qua cùng một điểm

Đây là cách tiếp cận rõ ràng nhất: xác định một điểm cụ thể và lần lượt chứng minh cả ba đường thẳng đều đi qua điểm đó. Khi hoàn tất, ta kết luận rằng ba đường đồng quy tại điểm đã chọn.

Ứng dụng thực tế của đồng quy

Tính chất đồng quy không chỉ là một khái niệm quan trọng trong hình học mà còn có nhiều ứng dụng thiết thực trong đời sống và các lĩnh vực kỹ thuật, thiết kế, xây dựng.

Kiến trúc và kỹ thuật xây dựng

Đồng quy được ứng dụng để xác định các điểm giao nhau chính xác của các trục, dầm, cột trong bản vẽ kỹ thuật, giúp đảm bảo độ chính xác và ổn định khi thiết kế các công trình có kết cấu đối xứng như mái vòm, cầu treo, nhà thờ hoặc các tòa nhà cao tầng.

Giao thông đô thị

Nguyên lý đồng quy được sử dụng trong thiết kế các nút giao thông trọng điểm, nơi nhiều tuyến đường gặp nhau tại một điểm, tạo thành các vòng xoay hoặc giao lộ hiệu quả. Việc xác định chính xác điểm đồng quy giúp tối ưu hóa dòng xe, giảm ùn tắc và tăng tính an toàn.

Các hệ thống định vị và đo đạc

Việc xác định vị trí đồng quy giữa nhiều đường truyền tín hiệu (ví dụ GPS hoặc radar) cũng giúp xác định tọa độ chính xác của một vật thể. 

Thiết kế đồ họa, kỹ thuật cơ khí hoặc robotics

Khái niệm đồng quy được sử dụng để lập trình chuyển động, xác định các điểm trọng yếu trong hệ tọa độ không gian.

Hội họa

Đồng quy là nguyên lý nền tảng của phép phối cảnh. Các họa sĩ từ thời Phục Hưng đã sử dụng các đường thẳng đồng quy về một điểm tụ (điểm tụ trong phối cảnh một điểm hoặc hai điểm) để tạo chiều sâu cho không gian hai chiều, giúp bức tranh trở nên chân thực và sống động hơn.

Quang học

Hiện tượng đồng quy cũng xuất hiện trong việc mô phỏng tia sáng. Các tia sáng phản xạ hoặc khúc xạ có thể được biểu diễn bằng các đường thẳng đồng quy tại tiêu điểm của thấu kính hoặc gương cầu, giúp mô tả cách ánh sáng hội tụ hoặc phân kỳ.

Các ví dụ về bài toán đồng quy

Ví dụ 1: Cho tam giác ABC vuông tại A, kẻ đường cao AH. Lấy điểm K thuộc đoạn thẳng HC. Qua K kẻ đường thẳng song song với AB, cắt AH tại D. Chứng minh AK, DK, BC đồng quy.

Giải:

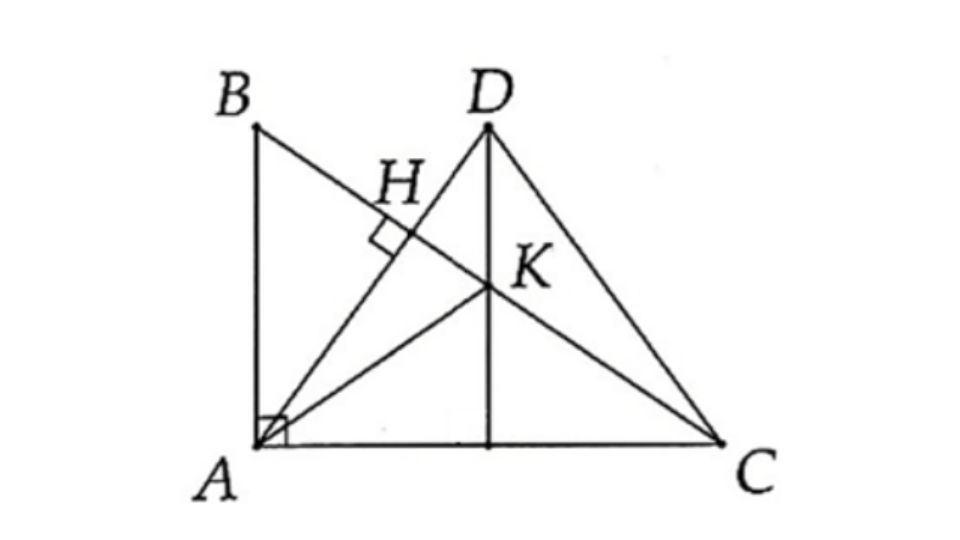
Vì AB ⊥ AC và DK // AB nên DK ⊥ AC.

Xét ∆ADC có: DK ⊥ AC, CH ⊥ AD và DK cắt CH tại K nên K là trực tâm ∆ADC.

Suy ra AK ⊥ CD.

Do đó ba đường thẳng AK, DK, BC đồng quy.

Ví dụ 2: Cho hình vẽ dưới, ABCD là hình bình hành. Chứng minh rằng:
a) EGFH là hình bình hành.
b) Các đường thẳng AC, BD, EF, GH đồng quy.

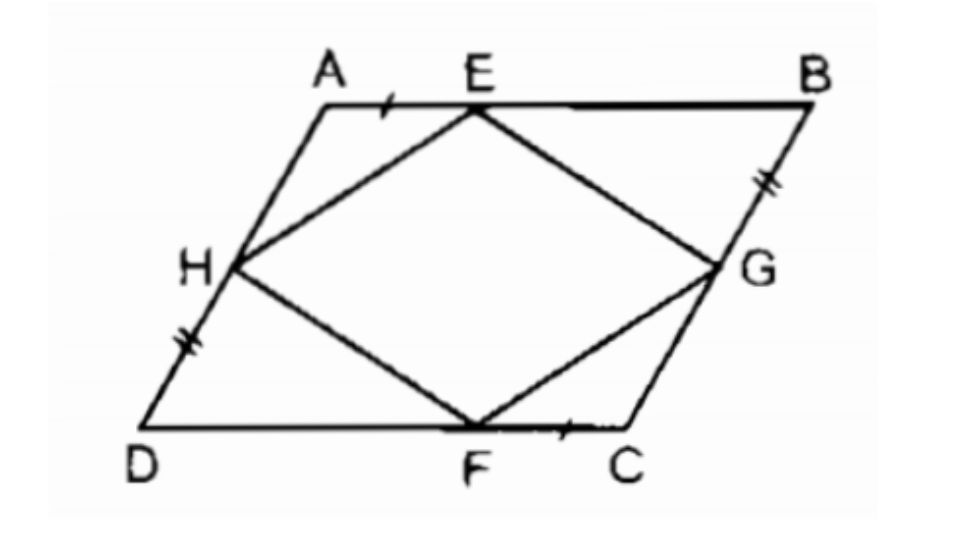
Giải:

a) Chứng minh rằng EG = HF, EH = GF.
b) Gọi O là giao điểm của AC và EF. Tứ giác AECF có AE = CF, AE // CF nên là hình bình hành. Suy ra O là trung điểm của AC, EF.
ABCD là hình bình hành, O là trung điểm của AC nên O là trung điểm của BD.
EGHF là hình bình hành, O là trung điểm của EF nên O là trung điểm của GH.
Vậy AC, BD, EF, GH đồng quy tại O.

Tạm kết

Tính chất đồng quy là một phần quan trọng và đầy thú vị trong hình học, giúp mở rộng hiểu biết về cấu trúc các hình phẳng và hình không gian, là nền tảng để giải quyết nhiều bài toán hình học từ cơ bản đến nâng cao. Hy vọng qua bài viết này, bạn đã hiểu rõ đồng quy là gì và có thể vận dụng hiệu quả trong học tập cũng như thực tiễn.

Bạn đang tìm kiếm một chiếc máy tính ổn định, bền bỉ và phù hợp cho nhu cầu học online, làm bài tập và thuyết trình? Laptop Dell chính là lựa chọn lý tưởng với hiệu năng mạnh, thiết kế gọn nhẹ và thời lượng pin ấn tượng. Xem tại:

Laptop Dell

Xem thêm:

• Học toán dễ dàng hơn bao giờ hết cùng 6 phần mềm giải toán online tốt nhất hiện nay
• Tổng hợp 11 phần mềm giải bài tập toán cao cấp tốt nhất cho học sinh, sinh viên