Tìm hiểu cách tính chu vi hình thoi và hướng dẫn giải các dạng bài tập thường gặp

Hình thoi là một dạng hình học cơ bản, thường xuất hiện trong cả chương trình học lẫn thực tế cuộc sống. Dưới đây, FPT Shop xin giới thiệu đến bạn các công thức và cách tính chu vi hình thoi một cách chi tiết và dễ hiểu.

Hình thoi là gì?

Trước khi đi vào cách tính chu vi hình thoi, thì chúng ta hãy cùng tìm hiểu khái niệm hình thoi. Đây là một loại tứ giác đặc biệt, có bốn cạnh bằng nhau và hai đường chéo vuông góc cắt nhau tại trung điểm của mỗi đường. Ngoài ra, hai đường chéo này còn đóng vai trò là đường phân giác của các góc trong hình.

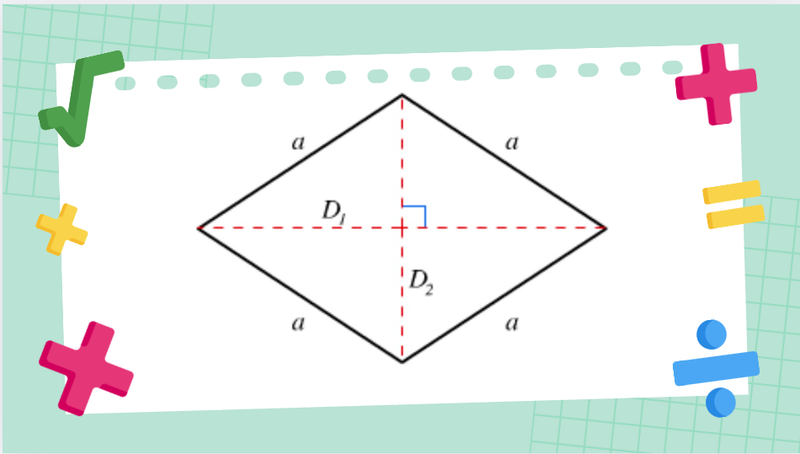
Trong trường hợp hình thoi có bốn góc vuông bằng nhau, nó trở thành một hình vuông. Điều này cho thấy hình vuông là một trường hợp đặc biệt của hình thoi vì vừa có bốn cạnh bằng nhau vừa có bốn góc vuông.

Tuy nhiên, không phải mọi hình thoi đều là hình vuông. Hình thoi chỉ cần thỏa mãn điều kiện về cạnh và đường chéo, không yêu cầu góc vuông.

Tính chất của hình thoi

Hình thoi và các tính chất của hình bình hành

Hình thoi kế thừa toàn bộ đặc điểm của hình bình hành: các cạnh đối song song và bằng nhau, các góc đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Tính chất góc trong hình thoi

Các góc đối trong hình thoi bằng nhau, và tổng bốn góc luôn bằng 360 độ, giống như mọi tứ giác khác.

Tính chất đường chéo

Hai đường chéo của hình thoi luôn vuông góc với nhau và giao nhau tại trung điểm mỗi đường, tạo thành bốn tam giác vuông bằng nhau.

Đường phân giác

Hai đường chéo không chỉ vuông góc mà còn đóng vai trò là đường phân giác của các góc trong hình thoi, chia mỗi góc thành hai phần bằng nhau.

Dấu hiệu nhận biết hình thoi

Dưới đây là các dấu hiệu nhận biết hình thoi được trình bày mạch lạc và dễ hiểu hơn:

• Tứ giác có 4 cạnh bằng nhau là hình thoi.
• Tứ giác có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường là hình thoi.
• Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
• Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
• Hình bình hành có đường chéo là đường phân giác của một góc là hình thoi.

Cách tính chu vi hình thoi đơn giản

Chu vi hình thoi được xác định bằng cách lấy độ dài một cạnh nhân với 4, bởi tất cả bốn cạnh của hình thoi đều có độ dài bằng nhau.

Công thức: P=a×4

Trong đó:

• P: Chu vi hình thoi.
• a: Chiều dài một cạnh hình thoi.

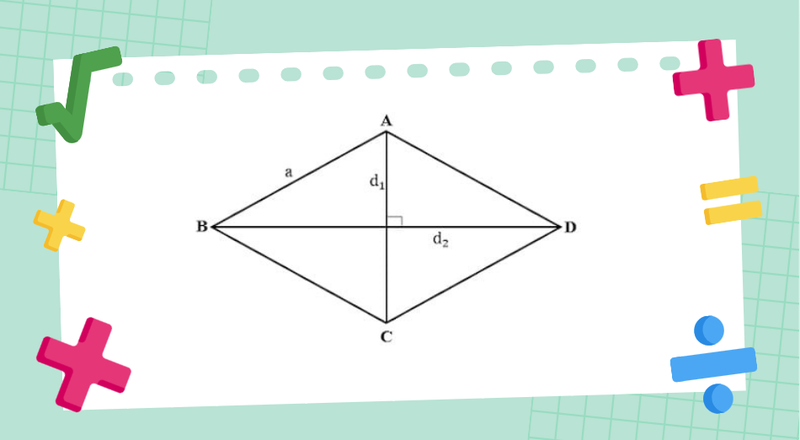
Lưu ý thêm:

Nếu đã biết chu vi của hình thoi, bạn có thể tính chiều dài một cạnh bằng cách lấy chu vi chia cho 4:

• a= P/4

​Ví dụ: Nếu chu vi của hình thoi là 20 cm, chiều dài một cạnh sẽ là:

a= 20/4 =5cm.

Cách tính này rất hữu ích trong các bài toán liên quan đến hình thoi trong thực tế và học tập.

Ví dụ: Một cánh diều dạng hình thoi có các cạnh bằng nhau và mỗi cạnh đều dài 9 cm. Hỏi chu vi của cánh diều hình thoi này là bao nhiêu?

Ta có a = 9 cm.

Suy ra, chu vi của tấm bìa hình thoi là: P = a × 4 = 9 × 4 = 36 (cm).

Ngoài việc nắm công thức xác định chu vi hình thoi, bạn cũng cần biết công thức tính diện tích hình thoi để giải các bài toán nâng cao. Diện tích được xác định bằng nửa tích độ dài của hai đường chéo.

Công thức: S= 1/2 x (d₁ x d₂)

Trong đó:

S: Diện tích hình thoi.

d₁, d₂ : Độ dài hai đường chéo.

Ví dụ:

Cho hình thoi có độ dài hai đường chéo lần lượt là 8 cm và 6 cm. Tính diện tích của hình thoi.

Lời giải:

Áp dụng công thức: S = 1/2 x (d₁ x d₂) = 1/2 x (8x6) = 24 cm²

Như vậy, diện tích hình thoi là 24 cm².

Công thức này không chỉ hữu ích trong việc giải các bài toán hình học mà còn có thể áp dụng trong thực tế để tính diện tích các hình thoi trong thiết kế hoặc đo đạc.

Một số dạng bài tập quen thuộc về tính xác định chu vi hình thoi

Trong phần kiến thức về chu vi hình thoi, các em học sinh sẽ được làm quen và thực hành các dạng bài toán phổ biến như sau:

• Dạng bài số 1: Tính chu vi của hình thoi khi biết độ dài cạnh.
• Dạng bài số 2: Tính độ dài các cạnh khi biết chu vi của hình thoi.
• Dạng bài số 3: Xác định chu vi hình thoi khi biết độ dài các đường chéo.

Dạng số 1: Cách tính chu vi hình thoi khi biết độ dài cạnh

Phương pháp giải: Các em chỉ cần xác định độ dài của một cạnh, sau đó áp dụng công thức xác định chu vi hình thoi bằng cách lấy độ dài cạnh nhân với 4.

• Ví dụ: Tính chu vi của hình thoi biết độ dài cạnh bằng 8 cm.
• Giải: Chu vi của hình thoi là: 8 × 4 = 32 (cm).

Dạng 2: Tính độ dài một cạnh khi biết chu vi của hình thoi

Phương pháp giải: Dựa vào công thức xác định chu vi hình thoi, có thể suy ra độ dài một cạnh bằng chu vi chia cho 4.

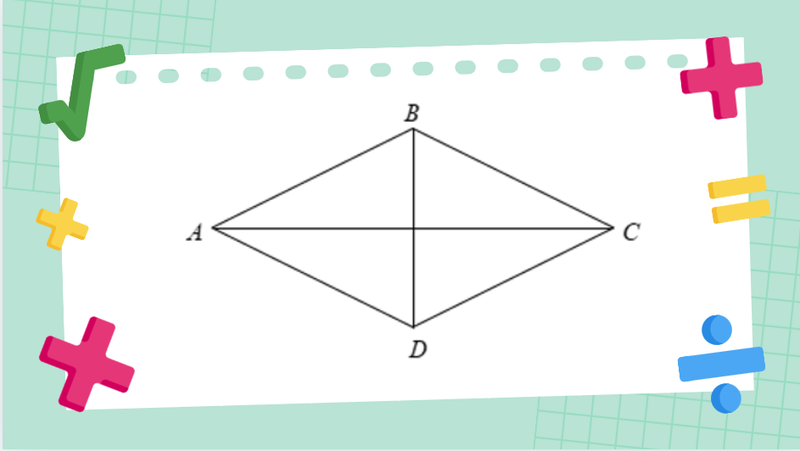
• Ví dụ: Tính độ dài các cạnh của hình thoi MNPQ khi biết chu vi của hình thoi là 48 cm.
• Giải: Gọi a là độ dài một cạnh của hình thoi.

P = a × 4 => a = P / 4 = 48 / 4 = 12 (cm)

Đáp án: Độ dài một cạnh của hình thoi MNPQ là 12 cm.

Dạng 3: Xác định chu vi hình thoi khi biết độ dài các đường chéo

Phương pháp giải:

Khi chỉ biết độ dài hai đường chéo, ta có thể sử dụng định lý Pythagoras để tìm độ dài cạnh hình thoi. Do hai đường chéo vuông góc và giao nhau tại trung điểm, mỗi nửa đường chéo sẽ là hai cạnh góc vuông của tam giác vuông. Độ dài cạnh hình thoi là cạnh huyền của tam giác đó.

Ví dụ:

Xác định chu vi hình thoi có độ dài hai đường chéo lần lượt là d₁= 12cm và d₂= 16cm

Giải:

Gọi cạnh hình thoi là a, hai đường chéo là d₁ và d₂

Theo định lý Pythagoras: a²= (d₁/2)^2 + (d₂/2)^2

Thay số:

a²= (12/2)² + (16/2)² = 6² + 8² = 36 + 64 = 100

a= √100 = 10 cm

Chu vi hình thoi: P = 4 x a = 4 x 10 = 40cm

Kết quả: Chu vi của hình thoi là 40 cm.

Phương pháp này rất hữu ích khi cần tính chu vi từ dữ kiện liên quan đến đường chéo, đặc biệt trong các bài toán thực tế hoặc hình học nâng cao.

Những mẹo hay để giúp bé nhớ lâu cách tính chu vi hình thoi

Củng cố kiến thức cơ bản về hình thoi

Để giải các bài tập về chu vi hình thoi một cách chính xác, bé cần nắm vững các kiến thức nền tảng như đặc điểm, tính chất của hình thoi và các công thức tính toán liên quan.

Hành động gợi ý: Bố mẹ nên kiểm tra kiến thức cũ của con thường xuyên. Nếu bé quên hoặc chưa hiểu rõ phần nào, hãy cùng bé ôn lại và giải thích chi tiết để tránh tình trạng lỗ hổng kiến thức khiến việc học sau này khó khăn hơn.

Thực hành và luyện tập thường xuyên

Học lý thuyết cần đi đôi với thực hành để giúp trẻ ghi nhớ và áp dụng kiến thức tốt hơn.

Hành động gợi ý: Sau khi bé hiểu được công thức tính chu vi của hình thoi, bố mẹ nên khích lệ bé làm thêm nhiều bài tập liên quan. Có thể:

• Giải bài tập trong sách giáo khoa hoặc sách bài tập.
• Tìm kiếm các bài tập nâng cao trên Internet.
• Thử sức với các đề thi mẫu để rèn luyện khả năng giải quyết vấn đề.
• Hạn chế cho bé sử dụng máy tính cầm tay để bé rèn luyện khả năng tính nhẩm tốt hơn.

Khuyến khích tư duy sáng tạo

Việc thực hành nhiều dạng bài tập khác nhau không chỉ giúp trẻ rèn luyện trí nhớ mà còn phát triển khả năng tư duy logic và sáng tạo trong học toán. Bố mẹ có thể tạo ra các tình huống thực tế, yêu cầu bé áp dụng công thức để giải quyết, chẳng hạn như tính chu vi của một khu đất hình thoi.

Bằng cách thực hiện đều đặn những mẹo này, việc học và làm bài tập của bé sẽ trở nên dễ dàng và hiệu quả hơn, giúp con tự tin hơn trong học tập.

Lời kết

Trên đây là những kiến thức cơ bản về cách tính chu vi hình thoi. Việc nắm vững những nền tảng này không chỉ giúp các bé hiểu rõ hơn về toán học mà còn tạo tiền đề vững chắc để học các kiến thức nâng cao.

Hãy trang bị cho mình một chiếc laptop mạnh mẽ, chất lượng chính hãng để hỗ trợ việc học toán và tìm kiếm tài liệu hiệu quả hơn. Đừng bỏ lỡ cơ hội sở hữu những chiếc laptop chính hãng, chất lượng cao với giá cả hấp dẫn tại FPT Shop.

Tham khảo các sản phẩm laptop Asus giá tốt tại đây:

• Laptop Asus

Xem thêm

• Hướng dẫn cách tính chu vi hình bình hành và vận dụng công thức với từng dạng bài tập, kèm ví dụ
• Công thức tính thể tích hình hộp chữ nhật: Bí quyết chinh phục toán học một cách dễ dàng