Ghi nhớ ngay cách tính chu vi của các hình học phổ biến vừa dễ học vừa dễ nhớ cho các bạn học sinh

Chu vi là một trong những khái niệm đầu tiên mà bất kỳ ai học toán đều phải làm quen. Từ những bài học toán cơ bản đến các bài toán nâng cao, chu vi đóng vai trò quan trọng trong việc giúp chúng ta hiểu rõ về kích thước và hình dạng của một hình học. Đối với những ai đang tìm hiểu cách tính chu vi cho các loại hình phổ biến, từ hình vuông, hình chữ nhật, hình tròn đến các hình đa giác phức tạp, bài viết này sẽ là một cẩm nang đầy đủ và chi tiết. Cùng khám phá các công thức tính chu vi và tìm hiểu lý do tại sao chu vi lại quan trọng đến vậy!

Cách tính chu vi của các loại hình học phổ biến

1. Cách tính chu vi hình vuông

Hình vuông là một loại hình tứ giác có bốn cạnh bằng nhau và các góc đều là góc vuông. Đặc điểm này giúp hình vuông trở thành một trong những hình đơn giản nhất để tính chu vi. 

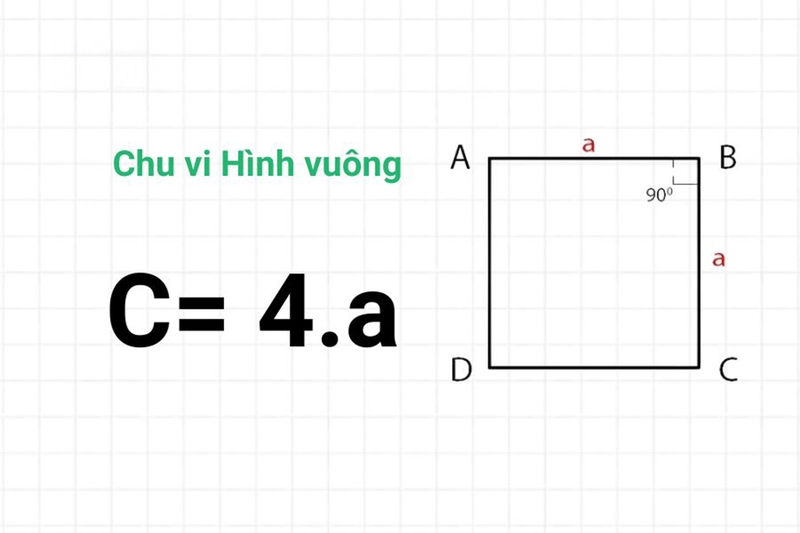
Công thức tính chu vi hình vuông:

• C=4×a

Trong đó:

a là độ dài của một cạnh hình vuông.

Ví dụ:

Cho hình vuông có độ dài cạnh là a=5 cm. Chu vi của hình vuông này sẽ được tính như sau:

C=4×5=20

Vậy, chu vi của hình vuông là 20 cm.

2. Cách tính chu vi hình chữ nhật

Hình chữ nhật là một loại hình tứ giác có hai cặp cạnh đối diện song song và bằng nhau, với các góc đều là góc vuông. Hình chữ nhật rất phổ biến trong thực tế, ví dụ như trang giấy A4 cũng có hình dạng chữ nhật.

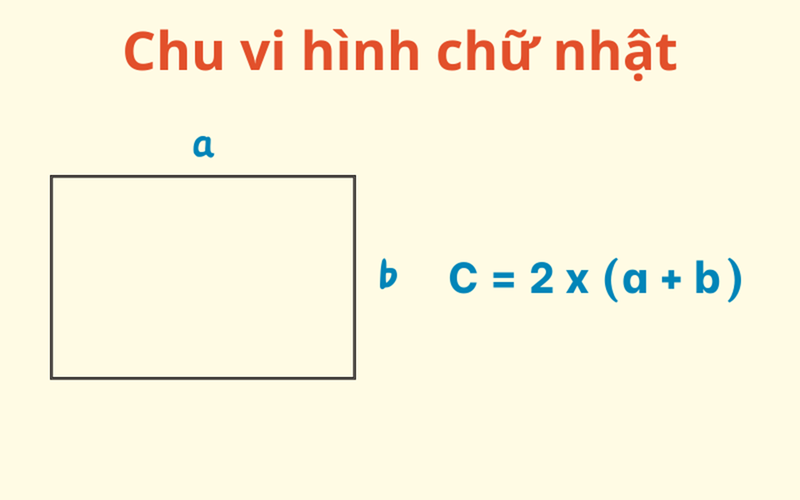
Công thức tính chu vi hình chữ nhật:

• C=2×(a+b)

Trong đó:

a là chiều dài.

b là chiều rộng.

Ví dụ:

Cho hình chữ nhật có chiều dài a=7 cm và chiều rộng b=3 cm. Chu vi của hình chữ nhật này là:

C=2×(7+3)=2×10=20

Vậy, chu vi của hình chữ nhật là 20 cm.

3. Cách tính chu vi hình tròn

Hình tròn là hình có tất cả các điểm trên bề mặt cách đều từ một điểm cố định, gọi là tâm. Hình tròn có một đại lượng đặc biệt là đường kính (d), gấp đôi bán kính (r).

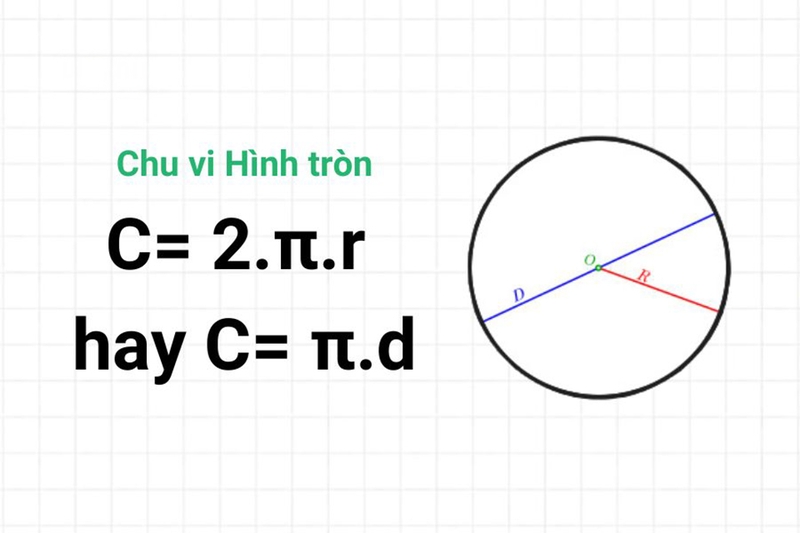
Công thức tính chu vi hình tròn:

• C=2πr hoặc C=πd

Trong đó:

r là bán kính của hình tròn.

d là đường kính (d=2r).

Ví dụ:

Cho hình tròn có bán kính r=5 cm. Chu vi của hình tròn sẽ là:

C=2×π×5≈31.4

Vậy, chu vi của hình tròn này là khoảng 31.4 cm.

4. Cách tính chu vi hình tam giác

Tam giác là một hình có ba cạnh và ba góc. Các loại tam giác như tam giác đều, tam giác vuông và tam giác cân có công thức tính chu vi giống nhau.

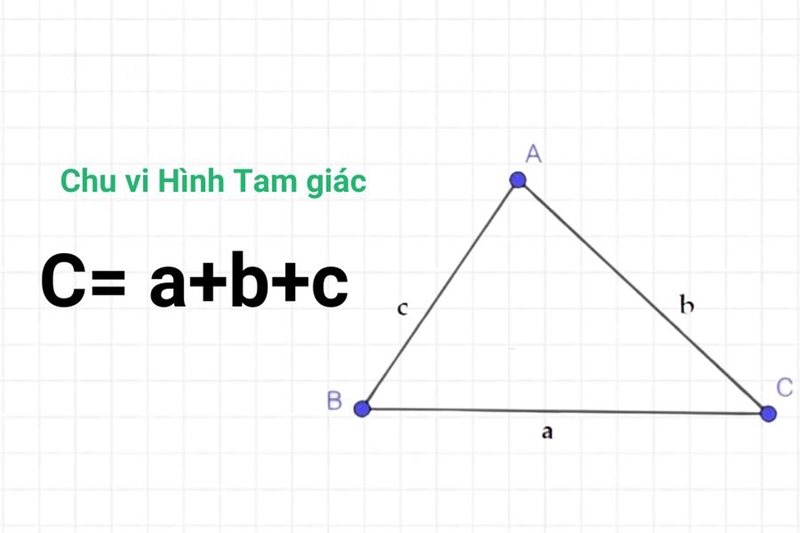
Công thức tính chu vi hình tam giác:

• C=a+b+c

Trong đó:

a, b, và c là độ dài của các cạnh của tam giác.

Ví dụ:

Cho tam giác có a=4 cm, b=5 cm và c=6 cm. 

Chu vi của tam giác là: C=4+5+6=15

Vậy, chu vi của tam giác là 15 cm.

5. Cách tính chu vi hình thang

Hình thang là một tứ giác có hai cạnh song song, được gọi là hai cạnh đáy, và hai cạnh không song song còn lại.

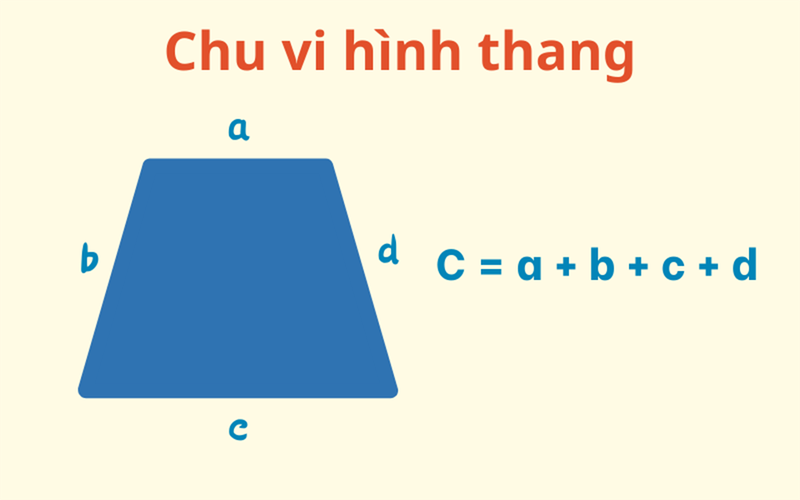
Công thức tính chu vi hình thang:

• C=a+b+c+d

Trong đó:

a, b, c, và d là độ dài các cạnh của hình thang.

Ví dụ:

Với hình thang có độ dài các cạnh lần lượt là

a=5 cm, b=7 cm, c=4 cm và d=6 cm, chu vi sẽ là: C=5+7+4+6=22

Vậy, chu vi của hình thang là 22 cm.

6. Cách tính chu vi hình elip

Hình elip là một hình có dạng tròn kéo dài, với hai bán trục chính (a) và bán trục phụ (b).

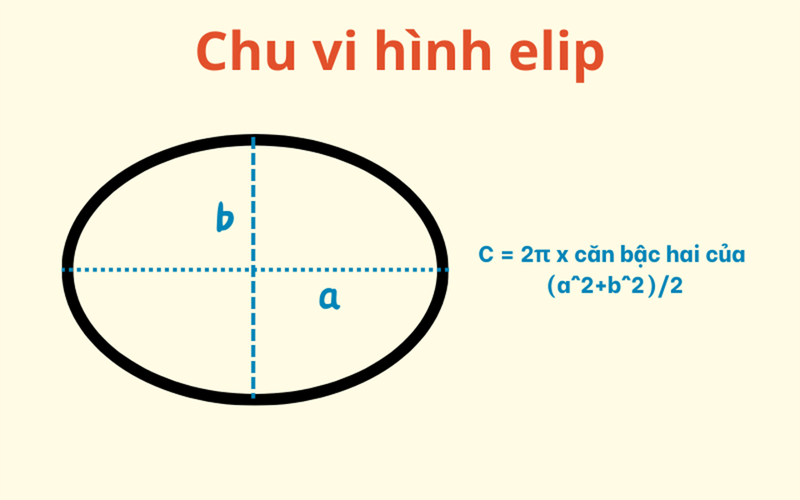
Công thức tính chu vi gần đúng của hình elip:

Trong đó:

a là bán trục lớn.

b là bán trục nhỏ.

Ví dụ:

Cho hình elip có bán trục lớn là a=6 cm và bán trục nhỏ là b=4 cm. Chu vi gần đúng sẽ là:

Vậy, chu vi của hình elip là khoảng 31.4 cm.

7. Cách tính chu vi hình lục giác đều

Hình lục giác đều là hình có sáu cạnh bằng nhau và các góc đều nhau, thường gặp trong tự nhiên như cấu trúc tổ ong.

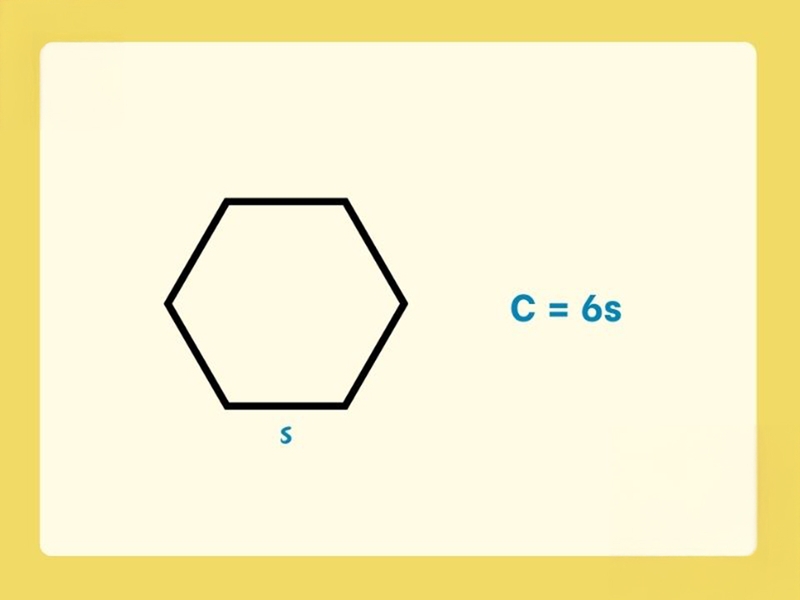
Công thức tính chu vi hình lục giác đều:

• C=6×s

Trong đó:

s là độ dài mỗi cạnh.

Ví dụ: Cho hình lục giác đều có cạnh s=4 cm. Chu vi của hình lục giác là:

C=6×4=24

Vậy, chu vi của hình lục giác là 24 cm.

Tạm kết

Bài viết này đã cung cấp cho bạn cái nhìn tổng quát và chi tiết về cách tính chu vi của các hình học cơ bản như hình vuông, hình chữ nhật, hình tam giác, và cả các hình phức tạp hơn như elip và lục giác đều. Hiểu rõ và nắm vững các công thức cách tính chu vi này sẽ giúp bạn tự tin trong việc giải quyết các bài toán hình học và ứng dụng trong thực tế, từ đo lường, tính toán, đến xây dựng, thiết kế.

Nâng cao hiệu quả học tập và tra cứu kiến thức nhanh chóng với một chiếc laptop chất lượng từ FPT Shop! Laptop không chỉ giúp bạn dễ dàng truy cập tài liệu, học trực tuyến mà còn là công cụ đắc lực để bạn làm bài tập, tìm kiếm thông tin và thực hành các bài toán mọi lúc, mọi nơi. Hãy đến FPT Shop ngay hôm nay để sở hữu một chiếc máy tính chính hãng, giúp bạn tự tin chinh phục mọi mục tiêu học tập và công việc!

Xem thêm:

• Cách tính chu vi hình chữ nhật: Hướng dẫn công thức chi tiết và bài tập áp dụng cho học sinh