Bội số là gì? Khác gì so với bội chung? Tìm hiểu bội số đối với toán học cấp cao

Hẳn bạn đã từng nghe qua các cụm từ như "bội số của 2", "bội số của 3" khi đang ngồi trên ghế nhà trường. Tuy nhiên, liệu bạn đã thực sự hiểu cặn kẽ bội số là gì và tại sao chúng lại quan trọng đến vậy? Đọc ngay bài viết để nắm vững khái niệm, qua đó xây dựng một nền tảng vững chắc cho hành trình chinh phục Toán học!

Bội số là gì?

Hiểu một cách đơn giản, bội số của một số nguyên a là kết quả của phép nhân số a đó với một số nguyên bất kỳ k. Nói cách khác, số b được gọi là bội số của a nếu tồn tại một số nguyên k sao cho b = a × k.

Ở đây, ta cần lưu ý:

• Số nguyên: Trong định nghĩa, a, b và k đều là các số nguyên (có thể là số dương, số âm hoặc số 0). Tuy nhiên, trong chương trình học phổ thông, khi nói đến bội số, chúng ta thường đề cập đến bội số của các số nguyên dương và bội số cũng thường là các số nguyên không âm.
• Vô hạn: Mỗi số nguyên (trừ số 0) có vô số bội số.

Ví dụ minh hoạ

Để dễ hình dung hơn về bội số là gì, hãy xem xét một vài ví dụ cụ thể như sau:

• Bội số của 2: Các số như 0, 2, 4, 6, 8, 10,... và -2, -4, -6,... đều là bội số của 2. Lý do là vì: 0 = 2 × 0; 2 = 2 × 1; 4 = 2 × 2; −2 = 2 × (−1).
• Bội số của 5: Các số 0, 5, 10, 15, 20,... và -5, -10,... đều là bội số của 5.
• Bội số của 7: Các số 0, 7, 14, 21,... và -7, -14,... đều là bội số của 7.

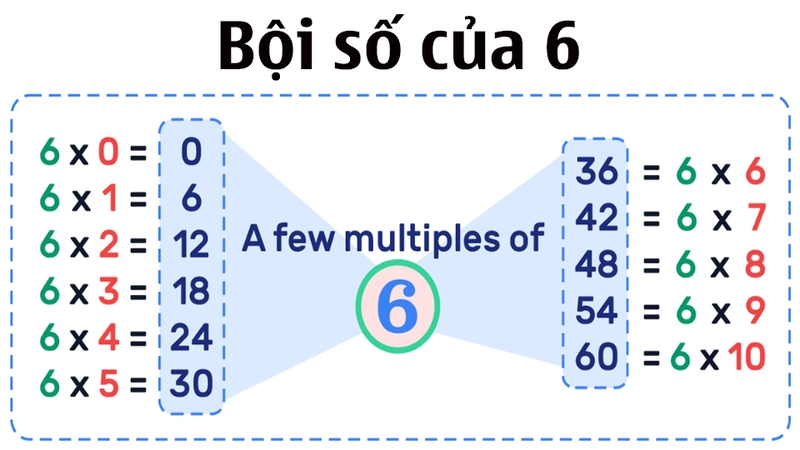
Tính chất của bội số là gì?

Tính chất chung của bội số

Sau khi hiểu rõ bội số là gì, việc nắm vững các tính chất của chúng sẽ giúp bạn áp dụng hiệu quả hơn trong việc giải toán:

(1) Số 0 là bội của mọi số nguyên khác 0: Vì với bất kỳ số nguyên a = 0, ta luôn có 0 = a × 0.

(2) Mỗi số nguyên khác 0 là bội của chính nó: Vì với bất kỳ số nguyên a = 0, ta luôn có a = a × 1.

(3) Các bội số của một số nguyên (khác 0) luôn cách đều nhau: Khoảng cách giữa hai bội số liên tiếp của một số a chính là ∣a∣. Ví dụ, các bội số của 3 là 0, 3, 6, 9,... mỗi số cách nhau 3 đơn vị.

(4) Nếu b là bội của a, thì −b cũng là bội của a: Nếu b = a × k, thì −b = a × (−k).

(5) Nếu b là bội của a và c là bội của a;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; thì tổng (b + c) và hiệu (b − c) cũng là bội của a:

• Nếu b = a × k1​ và c = a × k2​, thì b + c = a × k1 ​+ a × k2 ​= a × (k1 ​+ k2​).
• Và b − c = a × k1 ​− a × k2 ​= a × (k1 ​− k2​).

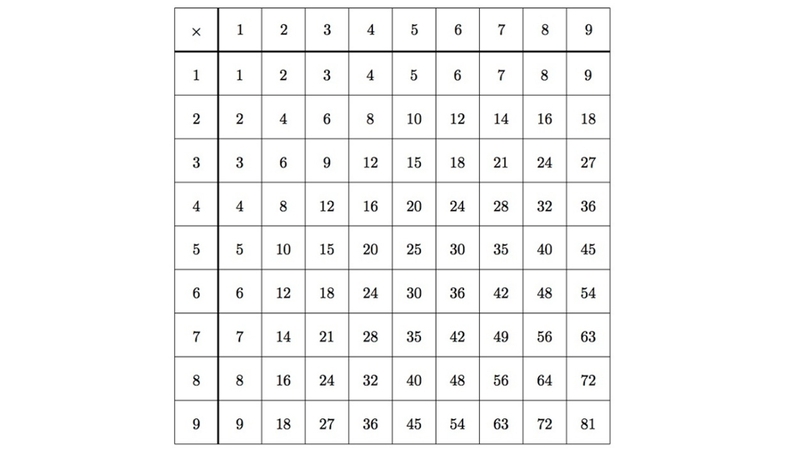
Mối quan hệ giữa bội số và phép chia hết

Một cách khác để định nghĩa bội số là gì chính là thông qua khái niệm phép chia hết:

Số b là bội số của số a khi và chỉ khi b chia hết cho a.

Điều này có nghĩa là khi chúng ta thực hiện phép chia b÷a, kết quả là một số nguyên và số dư bằng 0.

Ví dụ:

• 12 là bội của 3 vì 12 ÷ 3 = 4 (không dư).
• 10 không phải là bội của 3 vì 10 ÷ 3 = 3 dư 1.

Mối liên hệ này là cực kỳ quan trọng và thường được sử dụng để xác định một số có phải là bội của một số khác hay không.

Phân biệt bội số và bội chung

Như đã tìm hiểu ở phần "Bội số là gì?" trên, bội số của một số nguyên là tất cả các số có thể biểu diễn dưới dạng số đó nhân với một số nguyên khác. Nếu lấy một số a thì các số bội số của a có dạng: b = a × kb =a × k với k là số nguyên. Ví dụ, bội số của 3 là 6, 9, 12, 18,... là các số chia hết cho 3 không dư.

Trong khi đó, bội chung của hai hay nhiều số là những số nguyên có thể chia hết cho tất cả các số đó cùng một lúc. Nói cách khác, một số c là bội chung của các số a và b nếu c là bội số của cả a và b, tức là c chia hết cho a và c cũng chia hết cho b. Tập hợp bội chung của a và b là tập hợp các phần tử cùng thuộc tập các bội số của a và b. Ví dụ, bội chung của 3 và 4 là các số như 12, 24, 36,... vì đều cùng lúc chia hết cho cả số 3 và 4.

Tóm lại, bội số là khái niệm cho một số với một số gốc, còn bội chung đặc trưng cho những số chia hết đồng thời cho hai hoặc nhiều số. Bội chung là một tập hợp con trong tập bội số;;;;;;;;;;;;;;;;;;;;;;;;; nhưng liên quan đến nhiều số cùng lúc.

Bội số đối với toán học cấp cao

Khái niệm bội số là gì không chỉ dừng lại ở phạm vi số học cơ bản mà còn mở rộng và phát triển trong toán học cấp cao, đặc biệt là trong lý thuyết số, đại số trừu tượng và thậm chí cả trong khoa học máy tính.

Trong lý thuyết số

Lý thuyết số nghiên cứu sâu hơn về các tính chất của số nguyên, bao gồm cả bội số. Các khái niệm như hàm số học (ví dụ: Hàm ước số, hàm tổng ước số) và các định lý liên quan đến ước số và bội số đóng vai trò quan trọng trong việc hiểu cấu trúc của các số. Ví dụ, việc nghiên cứu các số hoàn hảo, số nguyên tố Mersenne đều liên quan mật thiết đến các ước số và bội số của chúng.

Trong đại số trừu tượng

Trong đại số trừu tượng, khái niệm bội số được tổng quát hóa thành các cấu trúc đại số phức tạp hơn như vành (rings) và mô-đun (modules). Trong một vành, bội số của một phần tử a là các phần tử có dạng ra (bội số bên trái) hoặc ar (bội số bên phải), trong đó r là một phần tử của vành. Các khái niệm như ideal (một dạng tổng quát hóa của tập hợp các bội số) là trung tâm của lý thuyết vành và có vai trò quan trọng trong việc xây dựng các trường mở rộng.

Trong khoa học máy tính, mật mã học

Trong khoa học máy tính, đặc biệt là trong các thuật toán liên quan đến số học modulo, bội số đóng vai trò then chốt. Phép toán modulo a (modn) trả về số dư khi a chia cho n. Khái niệm này liên quan trực tiếp đến bội số vì a ≡ b(modn) có nghĩa là a − b là bội của n, được ứng dụng rộng rãi trong:

• Thuật toán mã hóa: Các thuật toán mã hóa khóa công khai như RSA sử dụng các tính chất của số học modulo để đảm bảo tính bảo mật.
• Hàm băm: Các hàm băm thường sử dụng phép toán modulo để phân phối dữ liệu vào các vị trí bộ nhớ.
• Kiểm tra tính đúng đắn của dữ liệu: Các mã kiểm tra lỗi như mã CRC (Cyclic Redundancy Check) sử dụng các nguyên lý toán học liên quan đến bội số để phát hiện lỗi trong truyền dữ liệu.

Tạm kết

Bội số là một khái niệm toán học cơ bản nhưng có vai trò quan trọng trong nhiều phép toán và ứng dụng đời sống. Hiểu đúng bội số là gì và biết cách tìm bội số sẽ giúp bạn giải quyết các bài toán về số học nhanh chóng và dễ dàng hơn. Bên cạnh đó, kiến thức này cũng mở rộng sang các lĩnh vực khác như lập kế hoạch và xử lý dữ liệu, giúp nâng cao hiệu quả công việc.

Nếu bạn đang tìm mẫu laptop chất lượng, bền bỉ và hiệu năng mạnh mẽ để phục vụ học tập thì laptop Dell tại FPT Shop chính là lựa chọn hoàn hảo. Với nhiều mẫu mã đa dạng, công nghệ tiên tiến và ưu đãi hấp dẫn, Dell sẽ đồng hành cùng bạn chinh phục mọi bài học. Truy cập dưới đây để lựa chọn thiết bị hàng đầu cho mình:

Laptop Dell

Xem thêm:

• Tổng hợp đầy đủ công thức lượng giác dễ hiểu, dễ nhớ dành cho học sinh từ lớp 9 đến lớp 11
• Bảng công thức nguyên hàm đầy đủ nhất: Công thức cơ bản, nâng cao và phương pháp ghi nhớ hiệu quả