Mọi điều về Phương trình bậc 2 trong Toán học: Giới thiệu, cách bấm máy tính cùng bài tập vận dụng

Phương trình bậc 2 là một trong những chủ đề quan trọng trong bộ môn Toán học mà chắc chắn những bạn học sinh cấp 2 và cấp 3 đã không còn xa lạ. Kiến thức này không chỉ có liên quan đến phân môn Đại số mà còn là Hình học, và cũng vô cùng quan trọng trong chương trình học trung học cơ sở và trung học phổ thông, cũng như các ngành đại học có chuyên ngành Toán học.

Tuy nhiên, có hiểu biết về kiến thức là một chuyện, nằm lòng cách vận dụng kiến thức đó để áp dụng hiệu quả trong các bài toán thực tế thì lại là một chuyện khác. Vì thế, nếu bạn đang muốn hiểu rõ về định nghĩa, cách giải và những lưu ý khi giải kiểu phương trình này, hãy đọc ngay nội dung bài viết này nhé.

Tổng quan về phương trình bậc 2

Phương trình bậc 2 là một dạng phương trình (biểu thức toán học có chứa các biến số và các phép toán, được giải để tìm ra các giá trị của các biến để biểu thức trở nên đúng và có nghĩa) thuộc phần mục Đại số sơ cấp, thường được dạy lần đầu ở khối lớp 9 ở Việt Nam. Phương trình này có dạng tổng quát như sau: 

ax² + bx + c = 0

Trong đó:

• x là ẩn số cần tìm.
• a, b, c là các hệ số đã cho, với điều kiện a ≠ 0.

Một số ví dụ về phương trình bậc hai:

• x² - 5x + 6 = 0 với a = 1, b = -5, c = 6.
• 2x² + 3x - 2 = 0 với a = 2, b = 3, c = -2.

Các số a, b, và c là những hệ số của phương trình và có thể phân biệt bằng cách gọi tương ứng là: hệ số bậc hai, hệ số bậc một, và hằng số (hệ số tự do).

Vì phương trình bậc hai chỉ có một ẩn nên nó được gọi là phương trình "đơn biến". Phương trình bậc hai chỉ chứa lũy thừa của x là các số tự nhiên, bởi vậy chúng là một dạng phương trình đa thức, cụ thể là phương trình đa thức bậc hai do bậc cao nhất là hai.

Giải pháp cho các vấn đề tương tự phương trình bậc hai đã được con người biết đến từ năm 2000 trước Công Nguyên, với các bằng chứng chỉ đến các nhà toán học Babylon hoặc triều đại Ur thuộc Lưỡng Hà cổ đại.

Các cách giải phương trình bậc 2 phổ biến

Ngày nay, phương trình bậc hai có thể được giải bằng nhiều phương pháp như:

1. Dùng biệt thức

Trong công thức nghiệm của phương trình bậc hai, biểu thức dưới dấu căn được gọi là biệt thức. Đây chính là cách phổ biến nhất để giải các loại phương trình bậc 2 nói chung. Biệt thức thường được biểu diễn bằng chữ D hoa hoặc chữ delta hoa (Δ) trong bảng chữ cái Hy Lạp:

Δ = b² - 4ac

Ngoài ra, với b = 2b' thì ta còn có biệt thức thu gọn:

Δ′ = b’2 − ac (với Δ = 4Δ')

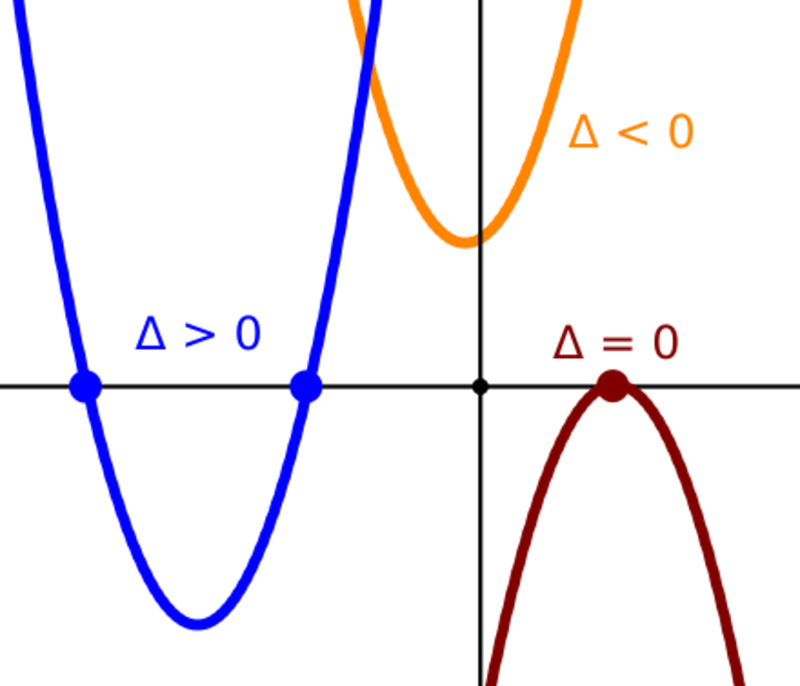
Phương trình bậc hai với các hệ số thực có thể có một hoặc hai nghiệm thực phân biệt, hoặc hai nghiệm phức phân biệt. Vì thế, dựa vào giá trị của biệt thức Δ, số lượng và bản chất của nghiệm phương trình sẽ chia làm 3 trường hợp:

• Nếu Δ > 0: phương trình có hai nghiệm phân biệt 
  • x₁ = (-b + √Δ) / (2a)
  • x₂ = (-b - √Δ) / (2a)
• Nếu Δ = 0: phương trình có một nghiệm kép
  • x = -b / (2a)
• Nếu Δ < 0: phương trình vô nghiệm thực, nhưng có hai nghiệm phức:
  • x₁ = (-b + i√|Δ|) / (2a)
  • x₂ = (-b - i√|Δ|) / (2a)  
    (Với i là đơn vị ảo, i² = -1).

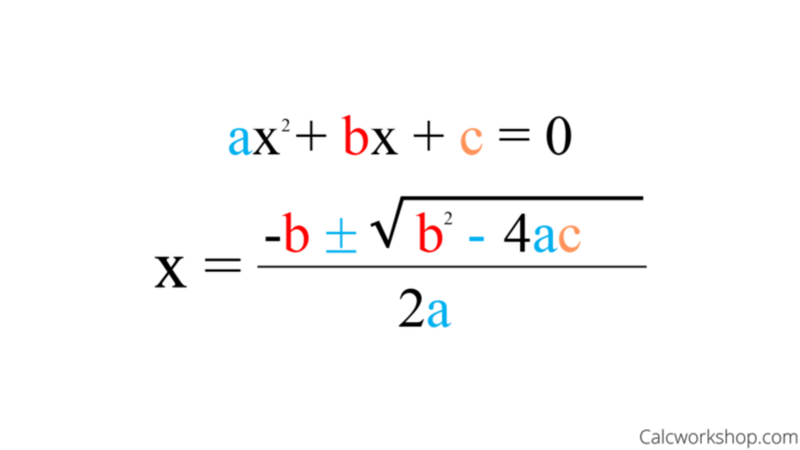
2. Phân tích thành nhân tử (nếu có thể) bằng cách kiểm tra

Phân tích thành nhân tử chính là một trong những cách đầu tiên mà học sinh ngày nay được dạy để giải phương trình bậc 2. Lưu ý rằng cách này chỉ có thể áp dụng đối với một vài ví dụ phương trình cụ thể.

Giải thích theo một cách đơn giản thì ta sẽ viết lại phương trình bậc 2 dưới dạng:

(px + q)(rx + s) = 0

Sau đó, ta có thể thực hiện một bước xem xét đơn giản để xác định các giá trị p, q, r, và s sao cho phù hợp với phương trình đầu. Sau khi đã viết được thành dạng này thì phương trình bậc hai sẽ thỏa mãn nếu px + q = 0 hoặc rx + s = 0. Giải hai phương trình bậc nhất này ta sẽ tìm ra được nghiệm.

3. Những cách thức khác

Ngoài những cách kể trên thì vẫn còn một vài cách thực hiện khác để giải một số ví dụ đặc thù của phương trình bậc 2 như: 

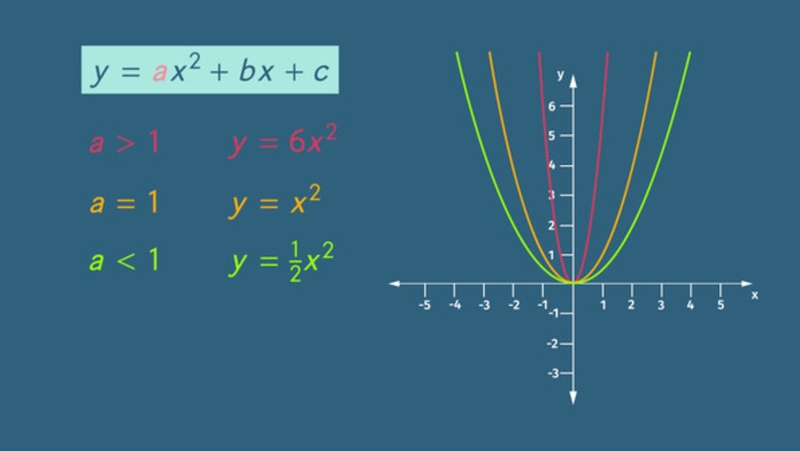
• Diễn giải bằng hình học: Sử dụng đồ thị parabol của hàm số bậc hai f(x) = ax² + bx + c để vẽ đồ thị hàm số y = ax² + bx + c, nghiệm là giao điểm với trục hoành.

• Nhân tử hóa đa thức bậc hai: Trong trường hợp đặc biệt b² = 4ac (hay Δ = 0) mà dẫn đến việc phương trình chỉ có một nghiệm phân biệt, có thể nhân tử hóa đa thức bậc hai thành ax² + bx + c = a(x + b/2a)².
• Phương trình bậc hai rút gọn: Chia cả hai vế cho a, điều này luôn thực hiện được bởi a khác 0, ta được phương trình bậc hai rút gọn có hệ số lớn nhất là 1 là x² + px + q = 0 (trong đó p = b/a và q = c/a).
• Phân tích thành nhân tử:

Nếu phương trình có thể viết dưới dạng tích của hai nhị thức, ví dụ như:

x² - 5x + 6 = (x - 2)(x - 3) = 0  
→ x = 2, x = 3

• Hoàn thành bình phương:

Một số phương trình không phân tích trực tiếp thì có thể biến đổi về dạng bình phương hoàn hảo, ví dụ như:

x² + 4x + 4 = 0  
⇔ (x + 2)² = 0  
→ x = -2

Ứng dụng thực tế của phương trình bậc 2

Phương trình bậc hai không chỉ là một chủ đề quan trọng trong toán học mà còn có nhiều ứng dụng thực tế trong nhiều lĩnh vực quan trọng khác nhau, tiêu biểu như:

• Ứng dụng trong vật lý và cơ học: 
  • Tính quỹ đạo chuyển động dạng parabol của vật thể.
  • Tính chuyển động rơi tự do của vật thể.
  • Tính toán tối ưu trong cơ khí như lực tác động và các hệ thống chịu tải trọng.
• Ứng dụng trong kinh tế và tài chính: 
  • Dự đoán lợi nhuận và tối ưu hóa chi phí trong mô hình kinh tế học.
  • Tính toán điểm hòa vốn của doanh nghiệp.
• Ứng dụng trong kỹ thuật và công nghệ thông tin: 
  • Xử lý đồ họa và mô phỏng hình học.
  • Tối ưu hóa thuật toán của trí tuệ nhân tạo và học máy.
  • Giải mã và mã hóa dữ liệu trong lĩnh vực an toàn thông tin.
• Ứng dụng trong kiến trúc và xây dựng 
  • Tính toán độ cong và sức chịu lực khi thiết kế cầu, mái vòm, tòa nhà.
  • Tính toán góc nghiêng và độ ổn định khi thiết kế đường dốc, cầu vượt hoặc hệ thống thoát nước.

Một số lưu ý khi giải phương trình bậc 2

Sau đây sẽ là một số lưu ý mà bạn nên nắm vững để giúp quá trình giải phương trình bậc hai trở nên hiệu quả và chính xác hơn.

• Xác định chính xác hệ số 
  • Trước khi giải, cần kiểm tra lại a, b, c để đảm bảo phương trình thực sự là bậc hai (a ≠ 0).
  • Nếu a = 0 thì phương trình sẽ trở thành bậc nhất (bx + c = 0), có cách giải khác hoàn toàn so với phương trình bậc 2.
• Tính toán biệt thức (Δ) cẩn thận 
  • Giá trị của Δ sẽ quyết định số nghiệm của phương trình.
  • Tránh sai sót khi tính b² - 4ac.
• Sử dụng công thức nghiệm đúng cách 
  • Kiểm tra dấu của a, b, c để tránh nhầm lẫn.
  • Nếu Δ là số chính phương (4, 9, 16, 25,...) thì có thể phân tích thành nhân tử để dễ dàng hơn.
• Kiểm tra nghiệm bằng cách thay vào phương trình ban đầu 
  • Sau khi tìm nghiệm, hãy thay lại vào phương trình để kiểm tra kết quả.
  • Nếu phương trình đúng, tức là nghiệm chính xác.
• Các phương pháp giải khác

Nếu cách giải này không hợp lý thì hãy thử nhiều cách giải khác để nhanh chóng tìm ra đáp án hơn.

Cách bấm phương trình bậc 2 trên máy tính

Dưới đây sẽ là các đường dẫn hữu ích nếu bạn đang muốn tìm hiểu thêm về cách bấm máy tính để giải phương trình bậc 2 đối với các loại máy tính phổ biến:

• Hướng dẫn giải bất phương trình bậc 2 trên máy tính Casio 570VN Plus
• Hướng dẫn tính toán phương trình cho máy tính Casio fx-580VN X
• Hướng dẫn đăng ký và sử dụng phương trình cho Casio CLASSWIZ-fx-880BTG

Một số bài tập vận dụng cho phương trình bậc 2

• Bài 1: Giải phương trình bậc hai sau: 2x² - 3x - 5 = 0

Cách làm:

• Phương trình có dạng tổng quát: ax² + bx + c = 0, với a = 2, b = -3, c = -5.
• Tính biệt thức Δ (Delta):

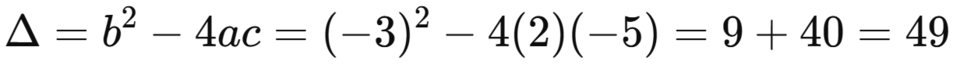
• Vì Δ > 0, phương trình có hai nghiệm phân biệt:

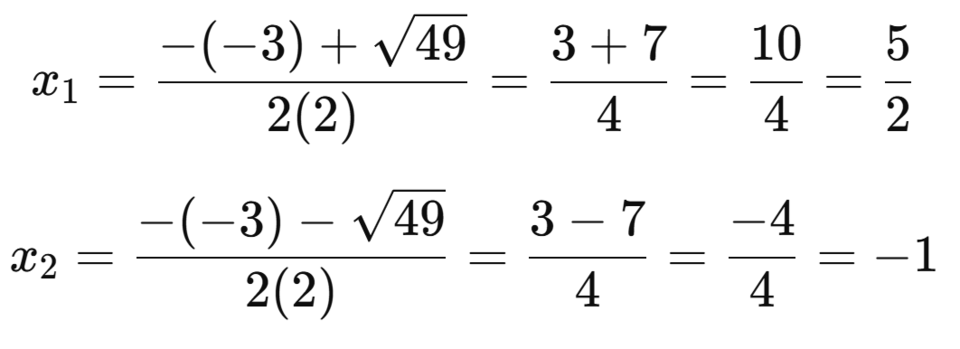
• Bài 2: Cho phương trình z2 + bz + c = 0 ẩn z và b, c là tham số thuộc tập số thực. Biết phương trình nhận z = 1 + i là một nghiệm. Tính T = b + c.

Cách làm:

• Theo lý thuyết thì một số phức bằng 0 khi và chỉ khi nó có phần thực và phần ảo cùng bằng 0.
• Vì z = 1 + i là một nghiệm của phương trình z² + bz + c = 0 nên ta có:

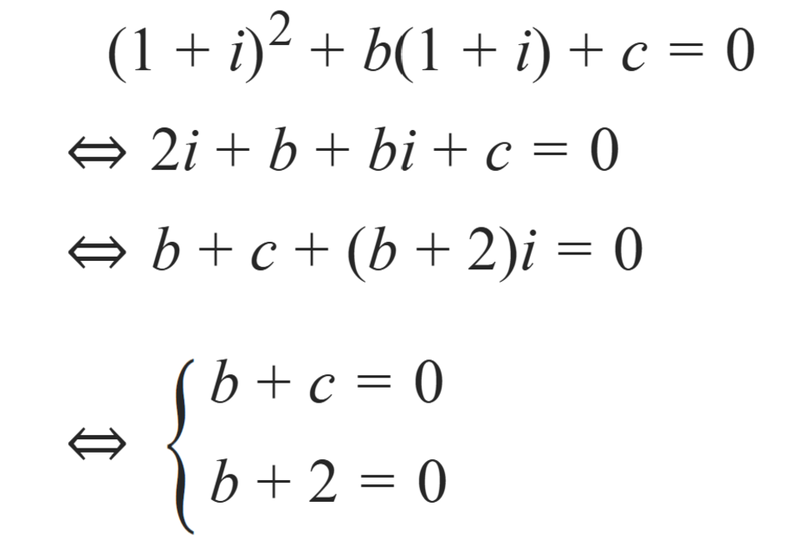
• Vậy T = b + c = 0.

Tạm kết

Trên đây là những thông tin có thể giúp bạn hiểu rõ hơn về phương trình bậc 2. Mong rằng bạn sẽ nắm bắt thật tốt những kiến thức Toán học bổ ích này!

Tại FPT Shop, bạn có thể tham khảo và chọn mua rất nhiều các thiết bị và phụ kiện hữu ích cho các cấp bậc học sinh khác nhau trên toàn quốc, đơn cử như những chiếc máy tính cầm tay quen thuộc cho việc giải các bài tập Toán. Hãy đến ngay cửa hàng FPT Shop gần nhất nếu bạn đang có nhu cầu mua sắm một chiếc máy tính khoa học nhỏ gọn nhưng vô cùng có ích nhé!

• Máy tính Flexio

Xem thêm:

• Mách bạn cách bấm SHIFT SOLVE 880 giải phương trình dễ dàng
• Top 5 app máy tính Casio online, thông minh trên điện thoại