Khám phá cách tính chu vi hình tứ giác đơn giản - ứng dụng được ngay trong đời sống!

Cách tính chu vi hình tứ giác không chỉ xuất hiện trong bài tập toán học mà còn mang tính ứng dụng cao trong thực tế. Từ việc đo đạc xây dựng cho đến thiết kế thời trang, hiểu rõ cách tính chu vi tứ giác sẽ giúp bạn dễ dàng giải quyết nhiều vấn đề thường gặp. Hãy cùng FPT Shop khám phá công thức cũng như mẹo tính chu vi nhanh chóng, chính xác ngay trong bài viết này!

Hình tứ giác là gì? Định nghĩa đơn giản nhưng dễ bị nhầm lẫn!

Hình tứ giác là một hình học cơ bản có bốn cạnh và bốn góc. Tổng số đo các góc bên trong của hình tứ giác luôn là 360 độ.

Bạn có thể chưa biết, nhưng có nhiều loại hình tứ giác khác nhau, bao gồm hình vuông, hình chữ nhật, hình thang và các dạng tứ giác không đều. Mỗi loại có những đặc điểm riêng về chiều dài cạnh và độ lớn góc, nhưng tất cả đều sử dụng một công thức chung để tính chu vi, đó là tổng chiều dài của bốn cạnh.

Nắm vững cách tính chu vi hình tứ giác sẽ giúp bạn áp dụng kiến thức này một cách hiệu quả trong học tập và trong nhiều tình huống thực tế hàng ngày đó!

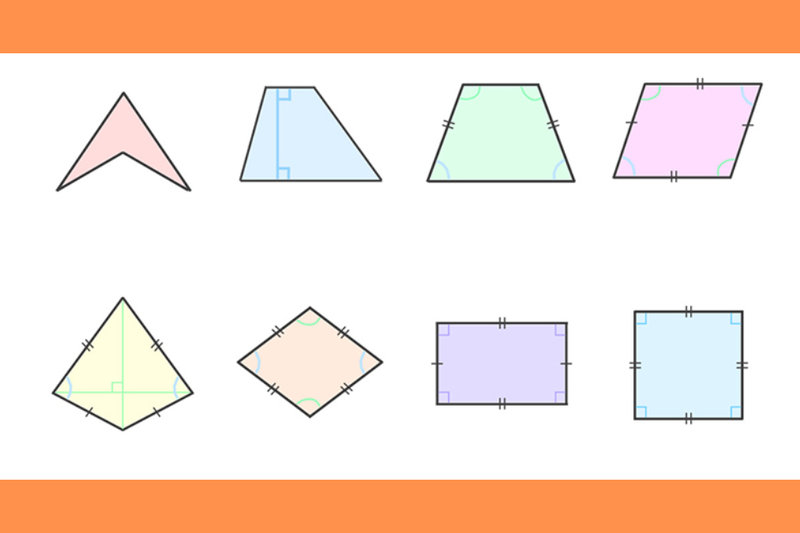
Khái niệm và công thức cơ bản tính chu vi của hình tứ giác

Hình tứ giác có thể được phân loại thành hai nhóm: tứ giác thông thường và tứ giác đặc biệt. Dưới đây là công thức để tính chu vi cho từng loại tứ giác khi giải quyết các bài toán mà bạn nên xem qua.

Phương pháp tính chu vi của hình tứ giác thông thường

Đối với các hình tứ giác thông thường, chu vi được tính bằng cách cộng tổng chiều dài của bốn cạnh. Công thức tính chu vi của tứ giác như sau:

P = a + b + c + d (đơn vị đo)

Trong đó:

P là chu vi của hình tứ giác.

a, b, c, d là độ dài của bốn cạnh khác nhau.

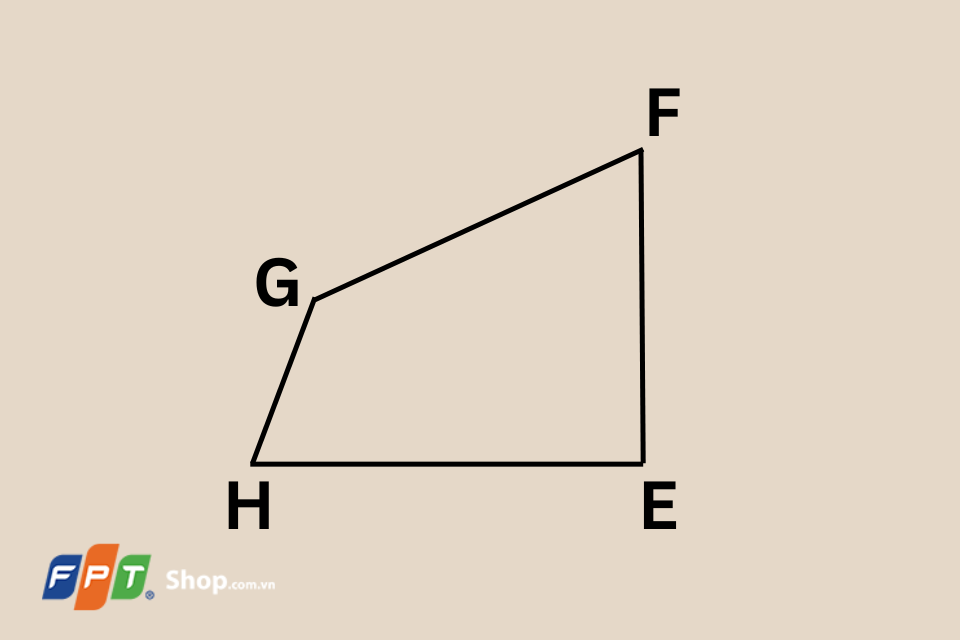
Ví dụ: Xét một tứ giác là hình thang có tên gọi là EFGH. Chiều dài các cạnh của hình thang này lần lượt là: cạnh EF = 5 cm, cạnh FG = 7 cm, cạnh GH = 4 cm và cạnh HE = 6 cm. Để tìm chu vi của tứ giác EFGH, bạn có thể sử dụng công thức sau:

P = EF + FG + GH + HE.

Thay các giá trị vào công thức, ta có: P = 5 + 7 + 4 + 6.

Tính toán cho ra kết quả: P = 22 cm.

Vậy chu vi của hình thang EFGH là 22 cm. Với công thức đơn giản này, việc tính chu vi hình tứ giác trở nên rất dễ dàng!

Phương pháp tính chu vi hình tứ giác đặc biệt - vô cùng đơn giản

Hình tứ giác đặc biệt bao gồm các loại như hình vuông, hình thoi, hình chữ nhật, hình bình hành và hình thang. Cách tính chu vi của những hình này thường rất đơn giản và dựa vào các công thức cụ thể như sau.

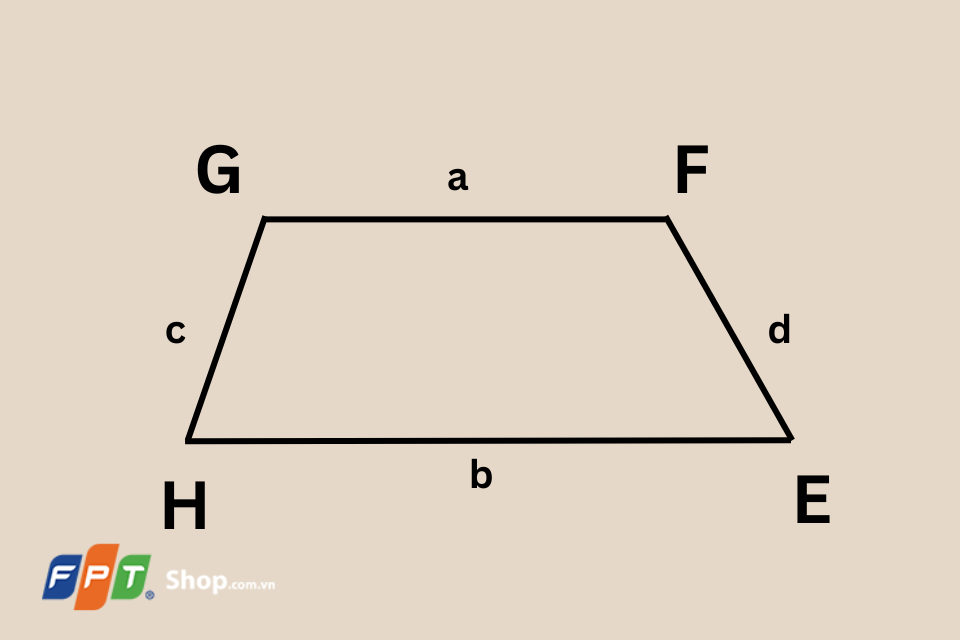
Hình thang

Công thức tính chu vi:

P = a + b + c + d

Trong đó:

P là chu vi của hình thang.

a, b, c, d đại diện cho chiều dài của bốn cạnh.

Ví dụ: Nếu có một hình thang với các cạnh có chiều dài lần lượt là 5 cm, 7 cm, 4 cm và 6 cm, thì chu vi sẽ là:

P = 5 + 7 + 4 + 6 = 22 cm.

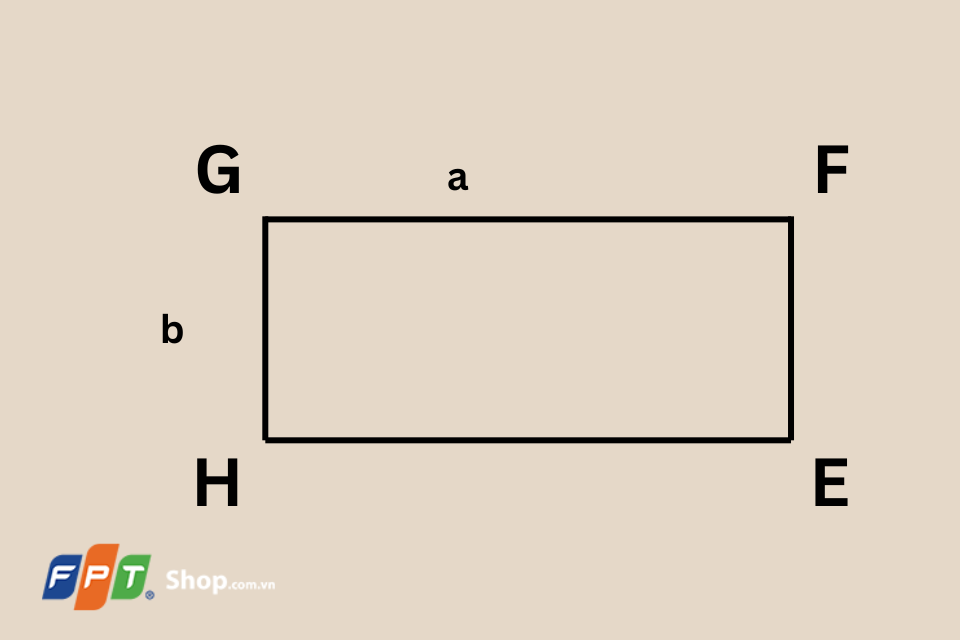
Hình bình hành và hình chữ nhật

Công thức tính chu vi:

P = 2 * (a + b)

Trong đó:

P là chu vi của hình bình hành hoặc hình chữ nhật.

a và b là độ dài hai cạnh khác nhau.

Ví dụ: Đối với một hình chữ nhật có chiều dài 8 cm và chiều rộng 5 cm, chu vi sẽ được tính như sau:

P = 2 * (8 + 5) = 26 cm.

Hình vuông và hình thoi

Công thức tính chu vi:

P = 4 * a

Trong đó:

P là chu vi của hình vuông hoặc hình thoi.

a là độ dài của một cạnh.

Ví dụ: Nếu một hình vuông có chiều dài cạnh là 6 cm, chu vi sẽ là:

P = 4 * 6 = 24 cm.

Ứng dụng cách tính chu vi hình tứ giác trong thực tế

Cách tính chu vi hình tứ giác không chỉ là kiến thức lý thuyết mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày. Dưới đây là một số trường hợp cụ thể mà bạn có thể áp dụng cách tính chu vi hình tứ giác:

• Thiết kế nội thất: Khi sắp xếp đồ nội thất trong nhà, bạn có thể gặp các khu vực hình tứ giác như phòng khách hoặc phòng ngủ. Việc tính chu vi giúp bạn xác định kích thước và vị trí hợp lý cho bàn, ghế, hoặc tủ, từ đó tối ưu hóa không gian sống.
• Quản lý bất động sản: Trong lĩnh vực đất đai, có rất nhiều khu đất với hình dạng tứ giác. Vậy nên, việc tính chu vi giúp chủ sở hữu biết được giới hạn đất của họ, từ đó có thể xác định diện tích và giá trị tài sản.
• Tổ chức tiệc: Khi tổ chức một buổi tiệc ngoài trời hoặc sự kiện, bạn có thể sử dụng các khu vực hình tứ giác như sân vườn hoặc sân thượng. Tính chu vi giúp bạn xác định không gian cho bàn ghế, thực phẩm và các hoạt động khác, từ đó đảm bảo sự thoải mái cho khách mời.

Nắm vững cách tính chu vi hình tứ giác sẽ giúp bạn áp dụng lý thuyết vào thực tế một cách hiệu quả, mang lại lợi ích cho công việc và cuộc sống hàng ngày!

Tạm kết

Hy vọng qua bài viết này, bạn đã nắm rõ cách tính chu vi hình tứ giác và nhận ra tầm quan trọng của nó trong cuộc sống hàng ngày. Việc hiểu biết về các hình tứ giác và cách tính chu vi không chỉ giúp bạn giải quyết bài tập một cách nhanh chóng mà còn mang lại lợi ích thiết thực trong các tình huống thực tế như thiết kế nhà cửa, làm vườn hay tổ chức sự kiện.

Nếu bạn muốn mở rộng thêm kiến thức về hình học và ứng dụng của nó trong đời sống, hãy ghé thăm FPT Shop. Chúng tôi cung cấp nhiều sản phẩm hữu ích hỗ trợ cho việc học tập và sáng tạo, đặc biệt điện thoại Xiaomi đang có giá rất tốt. Đội ngũ nhân viên thân thiện của chúng tôi luôn sẵn sàng hỗ trợ bạn tìm kiếm những sản phẩm phù hợp nhất. Đừng chần chừ, hãy đến khám phá và trang bị cho mình những kiến thức hữu ích ngay hôm nay!

Điện thoại Xiaomi

Xem thêm:

• Công thức tính diện tích hình thang và 4 lưu ý quan trọng khi làm các dạng bài tập liên quan
• Chia sẻ cách tính chiều dài hình chữ nhật cực dễ hiểu, chính xác và nhanh chóng